方法为先，思维为本

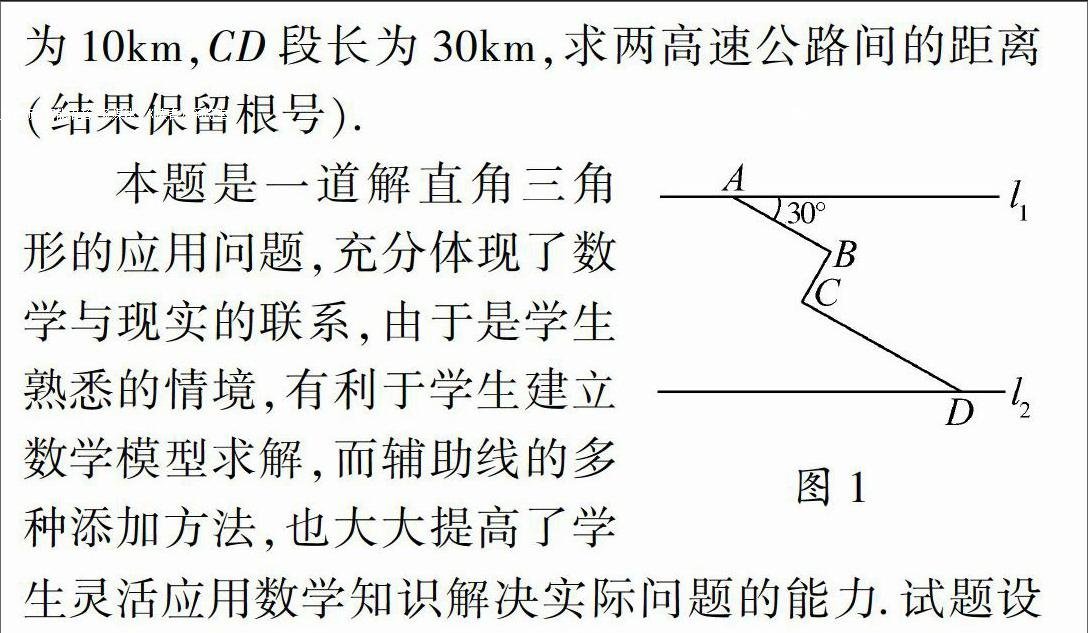
笔者参加了2014年安徽中考卷第18题的阅卷工作，从阅卷情况看，学生在解答过程中出现了许多值得我们教师反思的错误，现对学生出现的典型错误作具体分析，希望对今后的数学教学有一定的启示.

3对初中教学的启示

3.1立足教材，加强基础知识和基本能力的教学，努力提高学生的数学基本素养

通过添加辅助线解直角三角形，是课本中比较常见的题型，在安徽省中考试卷中，每一年都有类似的试题，试卷中却出现如此多样的失误，令人震惊.笔者认为这与部分教师在日常教学中轻视“双基”训练，片面的追求习题的难度脱不了关系.教学中应立足于教材，加强基础知识和基本技能的训练，让学生掌握学习数学的基本方法，知道解决具体问题的基本策略，切实提高课堂教学的实效.

3.2尊重现实，加强辅助线的教学，切实提高学生的构图能力

在几何图形中，辅助线就好比是沟通未知与已知的桥与船，巧妙地添加辅助线，解题就能达到“一桥飞架南北，天堑变通途”的效果.从阅卷情况看，学生要么是作不出辅助线，要么是作出了不合理的辅助线，反映出学生的构图能力较差.要解决这个问题，笔者认为在平时的教学中一定要有意识地通过几何试题的解决使学生明确以下两点：一是为什么要添加辅助线，添加辅助线要达到一个怎样的目的；二是为什么要这样添加辅助线，添加辅助线的依据是什么，还有没有其它的添加方法等.

3.3重视解题，注重一题多解，一题多变，尽力提升学生思维的品质

波利亚指出：“掌握数学就是善于解题.”在解题教学中，教师应适时地引导学生从不同的方法、角度、思维方式去观察、联想、分析，根据问题的特定条件探索出一系列的解题思路.在平时教学中，对于典型的例、习题，可以对其解答过程进行反思：问题的解决是否可以采用别的方法？辅助线的添加是否唯一？题目中的条件是否有冗余？条件与结论是否可以互换？是否可以变化引申等？通过这样一系列的思维活动，对典型例题进行一题多解、一题多变的训练，开拓学生思路，克服思维定势，切实提升学生的思维品质.

3.4重视交流，注意数学语言的规范化，努力提升学生的规范表达的能力

数学语言是数学思维和数学交流的工具.阅卷时我们发现有部分同学因解题不规范，辅助线添加几何语言叙述不准确、思维混乱而失分，这十分可惜.在教学中我们要重视细节教学（如书写格式的规范化、证明依据的规范使用等），加强学生数学语言的训练，让学生能够自觉地将文字语言、图形语言、符号语言相互转换，养成“严谨思维，规范表达”的习惯.

作者简介高厚良，男，1979年5月生，安徽蚌埠人，中学一级教师，主要从事中学数学教学及中考试题的研究，蚌埠市骨干教师，教学能手，曾获安徽省数学优质课一等奖，全国二等奖，近两年在省级以上刊物发表多篇文章.endprint