混频弱磁信号的采集与处理＊

门守强，许敬文，韩 磊，Christian Resagk

（1．西安工业大学 理学院，西安710021；2．西安工业大学 图书馆，西安710021；3．伊尔梅瑙工业大学 机械工程学院，伊尔梅瑙D-98684）

磁场断层成像是一种新兴的无损检测成像技术，通过对目标周围磁场测量，可以获得目标的电磁特性，包括电导率、介电常数和磁导率的分布，混合导电物质内部的电流分布、几何特性等．近年来，其原理及应用受到越来越多的关注［1-6］．磁场断层成像系统包括两部分：①为测量系统，即原始信号的采集；②为信号处理系统，包括信号的预处理和采用进化算法（如遗传算法）［5-6］等最优化方法重构目标的电磁特性或几何性质．成像效果的好坏首先取决于测量系统的优劣．在确定了测量系统所需要的磁传感器种类和数目之后，有必要对整个测量系统进行校准［7-8］，以期获得可靠的数据，通过信号的预处理建立数据库，为信号的后处理做好准备．

文中通过设计一个简单的校准系统，对一个沿方位角均匀分布的磁通门传感器环形阵列进行了校验．采用快速傅里叶变换对原始信号进行处理发现，校准系统中通电螺旋管的旋转频率并不固定，而是在一定的频率范围内进行波动，仅能得到有效的峰值频率，而不能获得信号的准确振幅．采用三角积分法，可以获得信号的功率谱密度，由此可以抽取信号的强度（或振幅），与快速傅里叶变换相反，此方法仅能得到信号的振幅．将快速傅里叶变换和三角积分法相结合，则可以获得信号的频率与振幅的完整信息，与精确的理论计算值定量符合．

1 校准装置

整个校准系统主要包括计算机、数据采集卡、电池组、螺旋管、直流电动机和磁传感器阵列．其中校准装置如图1所示，包括一个由绝缘铜线缠绕的螺旋管、恒定电流输出的电池组、由八个磁通门传感器组成的环形阵列．螺旋管由一层半径0．3mm的铜线在外径为1．75mm的塑料杆上缠绕而成，长度为40mm．螺旋管垂直固定在一个竖直的尼龙柱上，尼龙柱上端为电池盒，可以稳定地向螺旋管提供100．7mA的直流电流．八个相同的二维磁通门传感器（FXM 205［9］）以间距45°角均匀插在电路板上形成一个环形阵列，电路板则固定在圆筒外的基座上，其中传感器的两个线圈的几何中心与螺旋管的水平轴处于同一水平面内．螺旋管通过一根皮带与远处的直流电动机相连，由电机驱动，以2～6Hz的频率绕竖直轴旋转，与圆筒内装有两种不混溶的导电液体，并在竖直方向周期性振动时产生的法拉第不稳定性频率范围一致［10］．很明显，当螺旋管围绕竖直轴旋转时，环形阵列上的每个磁传感器都应该测得相同频率和振幅的交流信号，由此可以对传感器的灵敏度以及电路板对磁传感器的影响和传感器之间的交互作用进行校准．

实验中使用了一块Keithley的数据采集卡KPCI 3116对原始信号进行采集．KPCI 3116分辨率为16位，拥有32个模拟输入端口，采样率可达250kSps，保证了16个模拟输入端同时使用时每个通道的采样率能达到15kSps．

图1 校准系统Fig．1 Calibration system

2 结果及讨论

环形阵列上的磁传感器首先是单独校准的，随后是所有八个磁传感器都安装在电路板上时同时校准，用以确定各传感器分量之间的串扰和外部环境对不同方位传感器的干扰．通过调节电源的输出电压，可以控制电动机的转速，进而控制螺旋管的旋转频率，实验中旋转频率选为4．0Hz左右．此时，电池盒向螺旋管提供100．7mA的直流电流，采用2．5V的偏置电压、5kSps的采样率，采集40s的时间序列信号．其中前2s的单个传感器的信号如图2所示．可以看到，原始信号的纵向分量Br的强度是以伏特为单位．

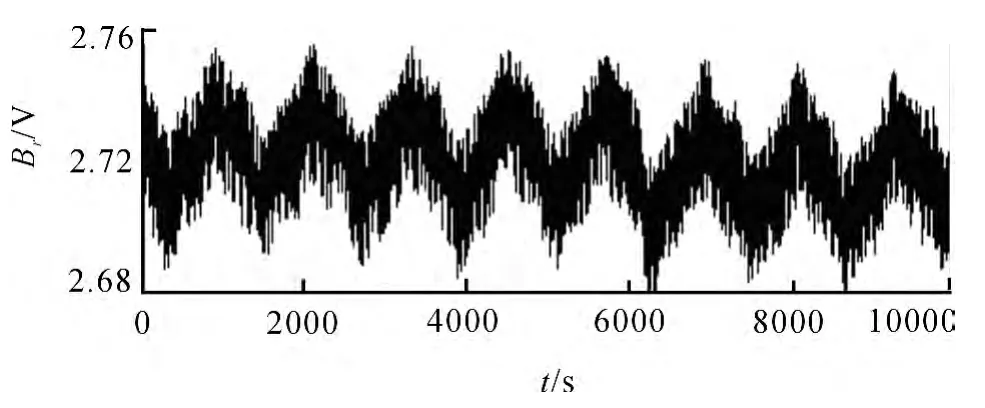
图2 5号传感器测得的磁场强度原始信号Fig．2 Raw signal of the magnetic field measured by Sensor 5

图2显示，尽管有一些高频的噪声，传感器感应到的信号是周期性的．为了获得激发磁场的频率和振幅，首先使用了截止频率30Hz的低通数字滤波器，然后又采用低频和高频分别为3．0Hz和6．0Hz的带通数字滤波器，对低通信号进行处理，结果如图3所示．经过处理，仍旧以纵坐标表示磁场强度，依照惯例，以磁感应强度的单位nT（纳特）来表示．如图4所示，可以看到，信号强度始终有一个比较大的起伏，幅度达到150nT，约为信号总强度的1／4．所以局域磁场强度的结果是不可靠的，不能由数字滤波获得，尽管可以从6s时间段内有25个峰值可估算旋转的频率约为4．1Hz．

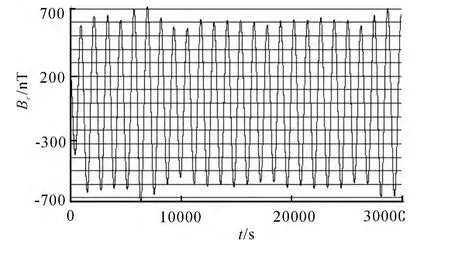
图3 低通滤波和带通滤波后5号传感器的时间序列信号Fig．3 Time series signal from Sensor 5，filtered by the low-pass and band-pass filter one by one

作为传统的信号处理方式之一，快速傅里叶变换也被用来处理此弱磁时间序列信号．与图2中的原始信号所对应的处理结果如图4所示．其中的实线为总时长为40s的信号的频谱．可以看到在频率4．0Hz附近有几个相近的峰值，显示出在40 s时间段内的弱磁信号或旋转频率并不固定，存在±0．2Hz左右的波动．另外，几个峰的强度仅为200nT左右，远小于精确的理论计算中607．5 nT，表明对整个信号进行快速傅里叶变换，只能得到精确的信号峰值频率，却不能获得准确的振幅．这时，需要将整个信号进行分割，分成不同的时间段．可以猜测，在某个时间段内，螺旋管的旋转频率可以看成是一个常数，从而由磁传感器测量的诱导弱磁信号也将会有一个恒定的频率．将40s长的时间序列分别分成2、4、10等份，对20s、10s、4s的信号分别作快速傅里叶变换，然后对相同时长的信号求平均，结果如图4所示．随着时间段的减小，峰值向理论计算值接近，到4s的间距时，已与理论计算值定量符合．但是，在此情况下，频率的分辨率相应地降低了，分别由40s时的0．025Hz降到了0．05Hz、0．1Hz和0．25Hz．所以，尽管将信号分成等长的时间段，可以获得准确的信号振幅，但频率分辨率的降低导致不能由此得到准确的峰值频率．所以，将一个信号分成多等份，不仅影响数据处理的效率，而且不能保证信号分割后能够获得令人满意的结果．

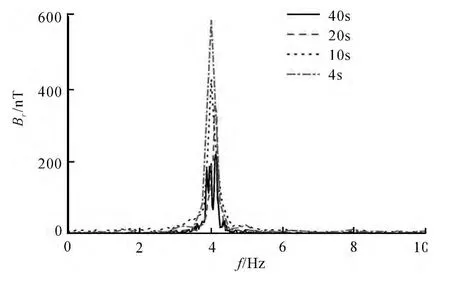
图4 5号传感器原始信号的快速傅里叶变换Fig．4 FFT result of the raw signal by Sensor 5

作为对比，采用matlab产生一个频率为4．1 Hz，振幅为10（任意单位），时长为40s的正弦信号，采样频率为5kSps，与磁传感器的采样率相同．添加白噪声后，原始信号如图5所示．插图中f为正弦信号的频率，而fs为采样率．

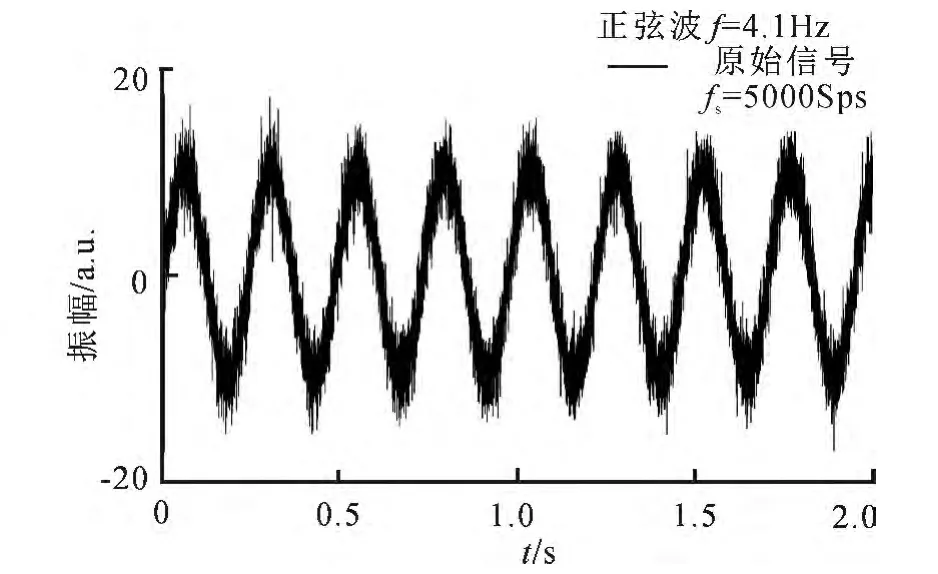
图5 由matlab产生的带有白噪声的正弦信号Fig．5 A sine wave with white noise generated by matlab

对正弦信号进行分割，将其分别分为10等份、4等份和2等份，经快速傅里叶变换处理后求平均，结果如图6（a）～（d）所示．从图中可以看出，对此单一频率的信号进行分割，只要给出的时间段所确定的频率分辨率不大于0．1Hz，无论信号分为几等份，都能得到准确的频率和振幅．然而，只要时间段低于某个下限（此处为10s），则既不能得到准确的振幅，又由于频率分辨率较低而得不到准确的频率，如图6（a）中4s的结果显示，峰值为7．5，对应的频率为4．0Hz，均与标准值10和4．1Hz有较大的偏差．

对于不同时间段对应于不同频率，但频率非常接近的时间序列信号，采用快速傅里叶变换进行处理也是不可行的．如图7（a-c）所示．三个携带白噪声的正弦信号，振幅均为2，频率分别为4．3Hz、4．2Hz和4．1Hz．

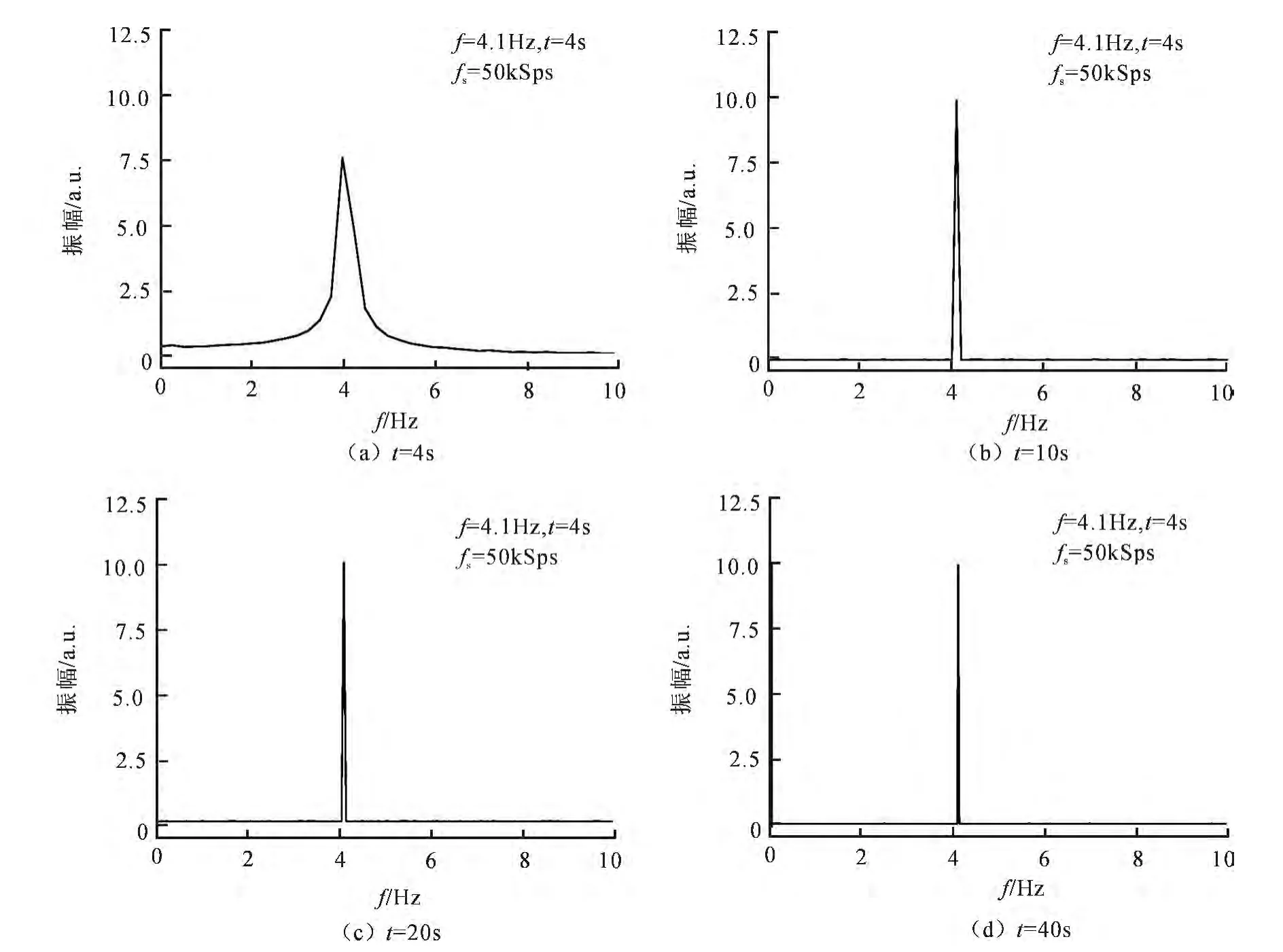
图6 时长40s的正弦信号分为10等份、4等份、2等份及原始长度的快速傅里叶变换Fig．6 FFT of the sinusoidal signals for 10 4s，4 10s，2 20sand the original 40s

其中，4．1Hz和4．3Hz的的信号时长均为10 s，而4．2Hz的时长为20s．对各自单一频率信号进行快速傅里叶变换，可以得到完美的频率和振幅，如图8（a-c）所示．然而，将4．1Hz、4．2Hz和4．3Hz的信号首尾相接，组成一个40s时长的原始信号，再用快速傅里叶变换进行，结果如图8（d）所示．尽管可以获得总信号的频率组成信息，但是，信号的振幅却是错的，远小于给定值2．

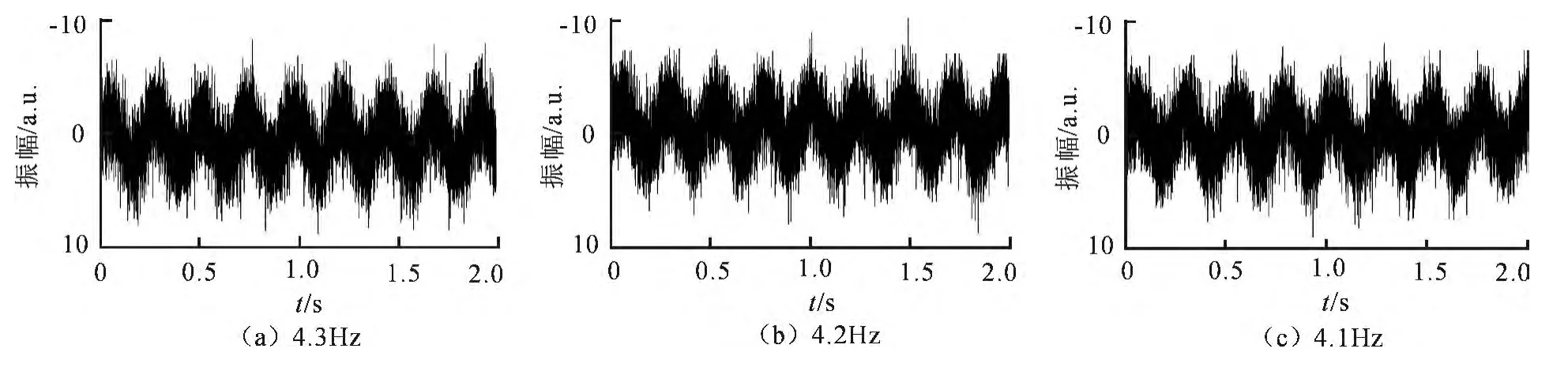
图7 携带白噪声的不同频率的正弦波，从左到右的频率依次为4．3Hz、4．2Hz、4．1HzFig．7 Sinusoidal signals with white noise for individual frequencies of 4．3Hz，4．2Hz and 4．1Hz

一个更好地处理方式是采用三角积分方法．即通过计算信号的能量，获得信号的功率谱密度，亦即信号强度的平方，对其开方即可获得信号的准确振幅．对实验数据进行处理，结果如图9所示．在外加电流分别为70．7mA、108．9mA 和197．0mA时，在螺旋管旋转过程中，由环形阵列在传感器位置对电流诱发的磁场进行50次测量，使用三角积分法处理后取平均，并计算各条件下的标准差．由图9可以发现，对每一个磁传感器而言，50次测量所得的标准差都远小于信号振幅的平均值，可忽略不计．但是，由各传感器测得的振幅的平均值相差较大，尽管都与理论计算值426．5nT、657．0nT和1188．5nT相接近，揭示了传感器的方位，或者说局域环境，包括地球磁场对传感器阵列存在一定程度的干扰．在经济条件许可的情况下，可以采用磁屏蔽减小外界的干扰．

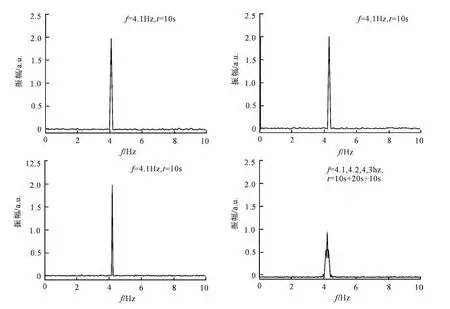
图8 不同频率与时长的三个正弦信号的快速傅里叶变换Fig．8 FFT diagrams of the three sinusoidal signals with different frequencies and lengths

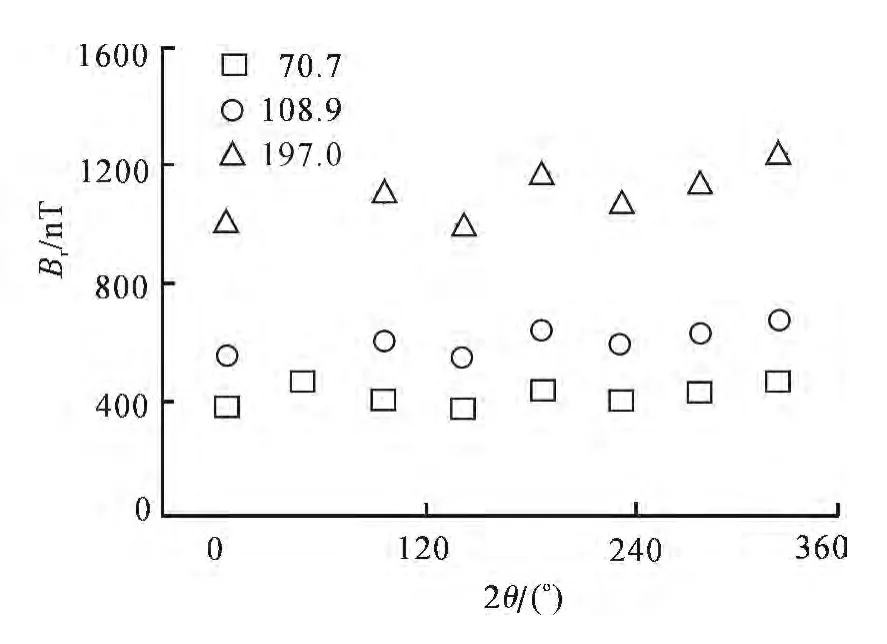
图9 采用三角积分法处理的不同电流下八个磁传感器测量的弱磁信号的振幅Fig．9 Amplitudes of weak magnetic signals for eight Dfluxgate sensors processed using trapzoidal integrations in the case of different electric currents imposed

3 结 论

1）为了校准磁传感器阵列的灵敏度，设计了一个竖直旋转式校准系统，使得每个传感器都能够测得相同频率和振幅的交流信号．

2）对于在不同时间段具有不同频率，但频率又非常接近的时间序列，采用快速傅里叶变换只能得到准确的峰值频率，不能获得信号的准确强度．与此相反，利用三角积分法，仅能获得准确的信号强度，无法抽取信号的峰值频率．

3）将两种处理方法相结合，对混频弱磁信号分别采用快速傅里叶变换和三角积分法进行处理，可以抽取此类时间序列的准确信息．

［1］ KYTE D J．Magnetic Induction Tomography and Techniques Using Eddy-Current Imaging［D］．Guildford：U-niversity of Surrey，1985．

［2］ PRÉMEL D，BAUSSARD A．Eddy-Current Evaluation of Three-Dimensional Flaws in Flat Conducting Materials Using a Bayesian Approach［J］．Inverse Problems，2002，18：1873．

［3］ SOLEIMANI M，TAMBURINO A．Shape Reconstruction in Magnetic Induction Tomography from Multifrequency Data［J］．International Journal of Information and Systems Sciences，2006，2（3）：343．

［4］ ABASCAL J F P J，LAMBERT M，Dominique Lesselier，et al．3DEddy-Current Imaging of Metal Tubes by Gradient-Based，Controlled Evolution of Level Sets［J］．IEEE Transactions on Magnetics，2008，44（12）：4721．

［5］ BRAUER H，ZIOLKOWSKI M，KUILEKOV M，et al．Surface Current Reconstruction Using Magnetic Field Tomography ［J］．IEEE Transactions on Magnetics，2004，40（2）：1398．

［6］ ZIOLKOWSKI M，BRAUER H，KUILEKOV M，et al．Reconstruction of the Interface Between Two Conducting Fluids Applying Genetic Algorithms［J］．IEEE Transactions on Magnetics，2004，40（2）：1248．

［7］ LASSAHN M P，TRENKLER G．Vectorial Calibration of 3DMagnetic Field Sensor Arrays［J］．IEEE Transation on Instrumentation and Measurement，1995，44（2）：470．

［8］ MERAYO J M G，BRAUER P，PRIMDAHL F，et al．Scalar Calibration of Vector Magnetometers［J］．Measurement Science and Technology，2000，11：120．

［9］ VERTESY G，GASPARICS A，SZOLLOSY J．High Sensitivity Magnetic Field Sensor［J］．Sensor and Actuators A-Physical，2000，85：202．

［10］ RESAGK C，MEN S，ZIOLKOWSKI M，et al．Magnetic Field Tomography on Two Electrically Conducting Fluids［J］．Measurement Science and Technology，2006，17：2136．