局部传感器发射功率约束条件下部分相干检测融合方法＊

徐振华，谢先斌，杨秀凯

（中国电子科技集团公司 第三十八研究所，合肥230088）

多传感器分布式检测融合技术在数据采集、环境监测、灾难预警与军事安全等方面的众多应用引起了国内外学术界和工业界众多研究者的高度关注．与集中式融合方式相比，分布式检测融合将各部传感器的判决作为自己的观测量进行假设检验，形成最终的判决．这种分布式数据处理减轻了融合中心的计算负担，便于工程实现．一方面无线传感器网络节点通常采用电池供电，能量有限且不易补充和更换，另一方面，多传感器分布式检测融合技术要求更高的发射和接收功率以及更为复杂的信号处理技术，这些都需要消耗更多的电池能量，因此如何高效地使用能量以达到优化系统的目标检测性能是一项亟待研究的内容．

大量的研究主要集中在基于并行拓扑结构的分布式检测融合方面，其各个传感器将独立检测的判决结果通过专用无线信道传输到融合中心，融合中心根据接收到的各路判决信息对目标的有无作出最终判决［1-4］．在实际应用中，上述这种并行拓扑结构的检测融合系统通常通过时分多址（TDMA）、频分多址（FDMA）和码分多址（CDMA）等传输方式实现．近几年来，基于多址接入信道传输方式的分布式检测融合方式由于具有带宽利用率高和能量消耗少的优点受到国内外研究者的重视［5-7］．基于并行拓扑结构，文献［8-9］的研究表明：在总发射功率约束条件下，利用多个同质传感器节点可以得到渐进最优二元分布式检测融合系统性能，系统希望获得较多的局部检测融合判决信息来提高探测性能．文献［10-11］分别利用系统的J散度作为优化对象和粒子群优化理论研究了最优功率分配问题，上述方法计算量很大，不利于工程实现．基于多址接入信道传输方式，在总发射功率约束条件下，文献［12-13］分别研究了最优量化函数和最优局部映射准则问题，其研究表明：在相同总发射功率约束条件下，多址接入信道传输方式不但可以大大提高带宽利用率，而且其对应的检测性能优于并行拓扑结构．在局部传感器发射功率约束条件下，文献［14］的研究表明：融合中心的最优融合规则可以简化为关于接收信号的门限检测．文献［15］提出了一种基于偏移系数极大化和NP的多址信道检测融合新方法．然而，上述研究大都假设相干检测，在工程实践中，完全相干检测的条件假设过于理想，为了便于工程应用，文中研究传感器局部发射功率受限约束条件下部分相干检测融合问题．

1 衰落多址信道分布式部分相干检测融合模型

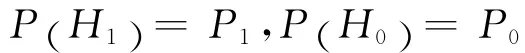
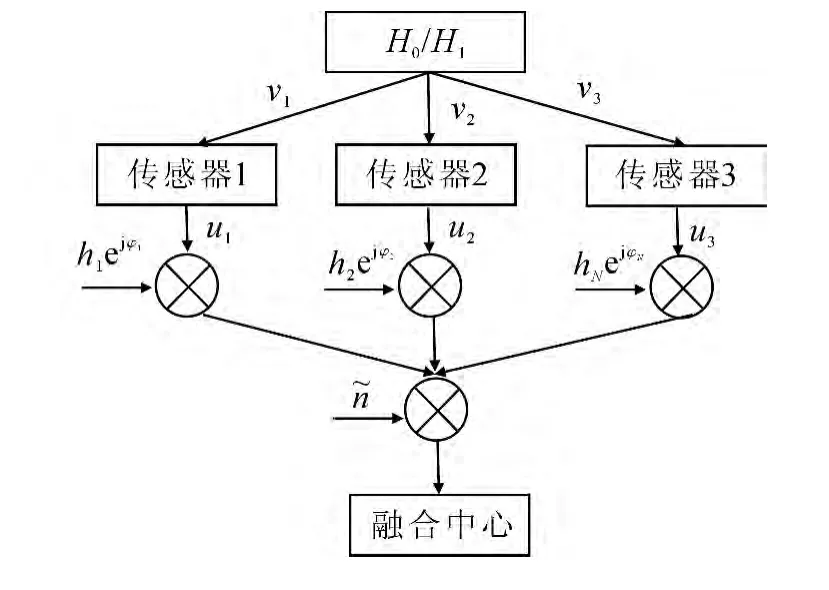
图1 分布式部分相干检测融合模型Fig．1 Distributed and partially coherent detection system model

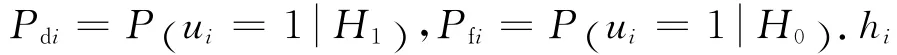
传感器节点通常采用电池供电，能量有限且不易补充和更换．在传感器节点能量约束条件下，融合中心接收到的信息可表示为

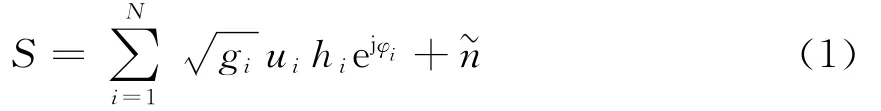
其中：gi≥0（1≤i≤N）为乘性加权系数（取根号形式是为了下文计算的方便），在传感器节点能量约束条件下，gi用于调制对应判决信息ui的脉冲波形的幅度．

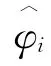
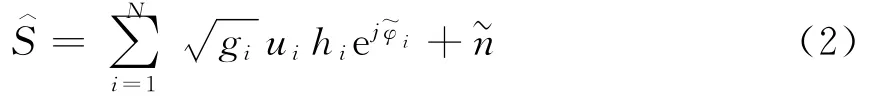
事实上，吉洪诺夫（Tikhonov）概率分布已经被广泛用于表征相位误差的随机性．因此，相位同步误差的概率密度函数可用吉洪诺夫概率分布可表示为

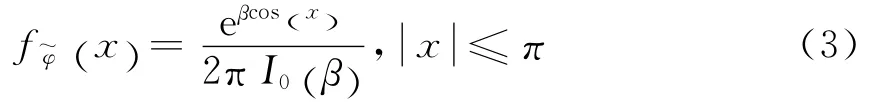
In（x）为第一类n阶修正贝塞尔函数，此处为零阶贝塞尔函数．参数β≥0称为环路信噪比，环路信噪比的大小取决于锁相环的相位同步精度，其值越大，同步精度越高．因此当β→＋∞时，说明相位同步误差趋向于零，此时融合中心对检测判决信息的接收方式为相位相干接收．

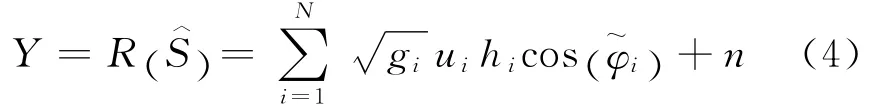
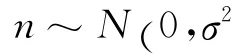
2 基于偏移系数极大化的局部发射功率约束部分相干检测融合

检测系统的偏移系数作为评价检测性能的标准，可以被看作决策融合系统的输出信噪比，其值越大，说明系统的检测性能越好．尽管基于偏移系数准则设计检测系统是次优的，但是由于偏移系数的计算仅需要检测统计量的一阶矩和二阶矩信息，便于实际应用，因而被广泛用于最优检测器的设计［18-19］．需要说明的是，在实际应用中的许多情况，利用偏移系数准则设计的检测器性能逼近最优似然比检测器，比如高斯噪声背景下的高斯信号检测问题．

偏移系数［19］定义为

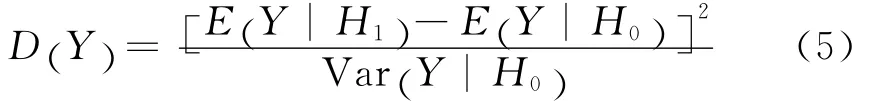
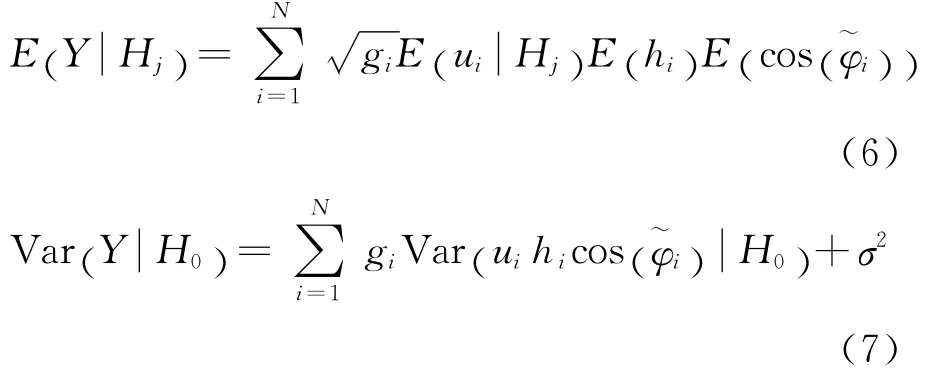
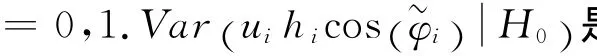
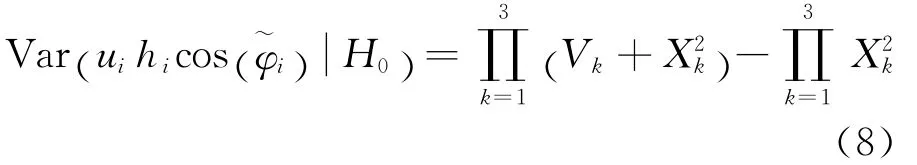
当信道增益统计信息已知时，局部发射功率约束条件下分布式部分相干检测融合的性能优化问题可建模为

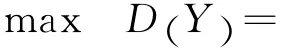
3 性能仿真与分析

为了对文中提出的信道增益统计信息已知时的局部发射功率约束部分相干检测融合方法进行性能评估，做如下仿真试验：假设某衰落多址接入信道部分相干检测融合系统由N＝8个局部传感器节点和一个融合中心组成．局部传感器节点对同一目标检测概率｛Pdi｝＝ ｛0．5，0．3，0．4，0．35，0．5，0．45，0．6，0．7｝，为了方便性能比较且不失一般性，虚警概率｛Pfi｝＝ ｛0 ．05｝，i＝1，2，…，N，先验概率P0＝0．5．融合系统第i个局部传感器的发射功率约束Qi＝1，总功率约束

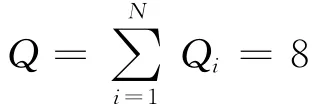
当虚警概率PF＝0．05，β值不同时信噪比与检测概率之间的关系如图2所示．文中提出的信道增益统计信息已知时的局部发射功率约束部分相干检测融合方法的接收机特性曲线（Receiver Operating Characteristci，ROC）如图3所示．考虑信道增益信息完美已知和信道增益统计信息已知两种情况，图4给出了当虚警概率PF＝0．05，β＝10时信噪比与检测概率之间的关系，作为对比，图中也画出了文献［4］中基于并行网络拓扑结构的最优似然比方法（PAC-LRT）的检测性能．

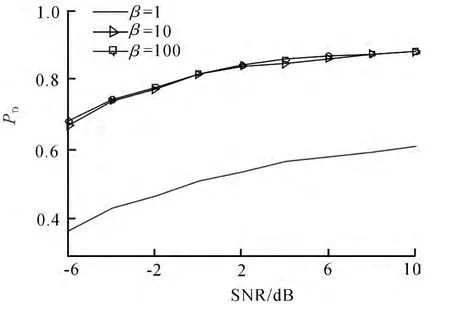
图2 β值不同时信噪比与检测概率之间的关系（PF ＝0．05）Fig．2 Relationship between SNR and detection probability with differentβ（PF ＝0．05）

从图2可以看出，随着信噪比的增大，系统的的检测性能提高，当环路信噪比β＝10，系统在低信噪比时的检测性能优于融合前的最优局部检测器性能．在实际中，环路信噪比β＝10对于系统来说显然不是一个苛刻的要求．在信噪比和虚警概率给定时，随着β值的增大，融合系统的检测性能随之提高，这是因为β值越大说明相位同步误差越小，所以检测性能就越好．

从图3可以看出，考虑局部传感器发射功率约束，在低信噪比和低虚警概率条件下，文中提出的方法能显著提高系统的检测概率．从图4可以看出，当信道增益信息完美已知时系统的检测性能是最优的，但是在实际中这种情形很难实现，而考虑信道增益统计信息已知这种次优情况，尽管检测器性能有所损失，但是其有利于工程实现．

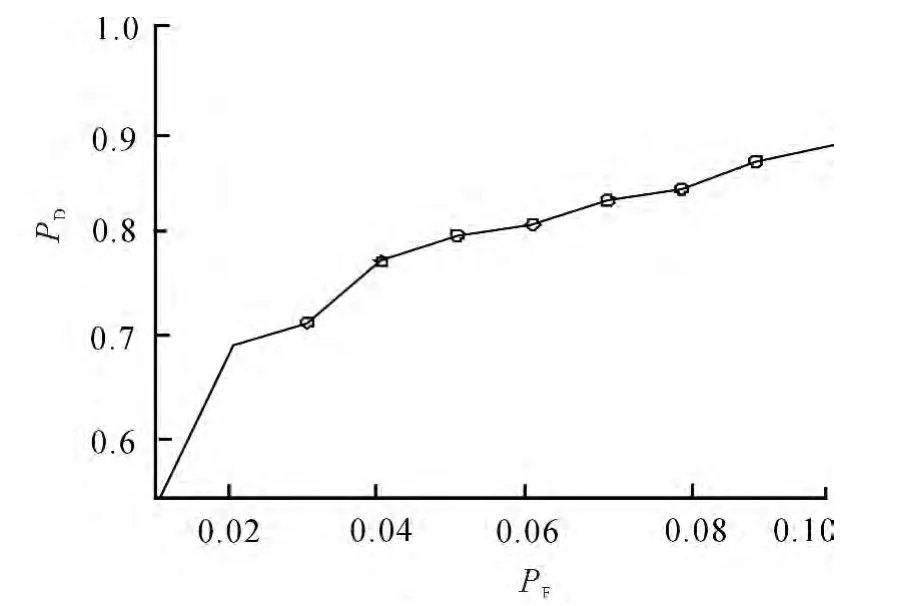
图3 ROC曲线 （β＝10，SNR＝0dB）Fig．3 ROC curves（β＝10，SNR＝0dB）

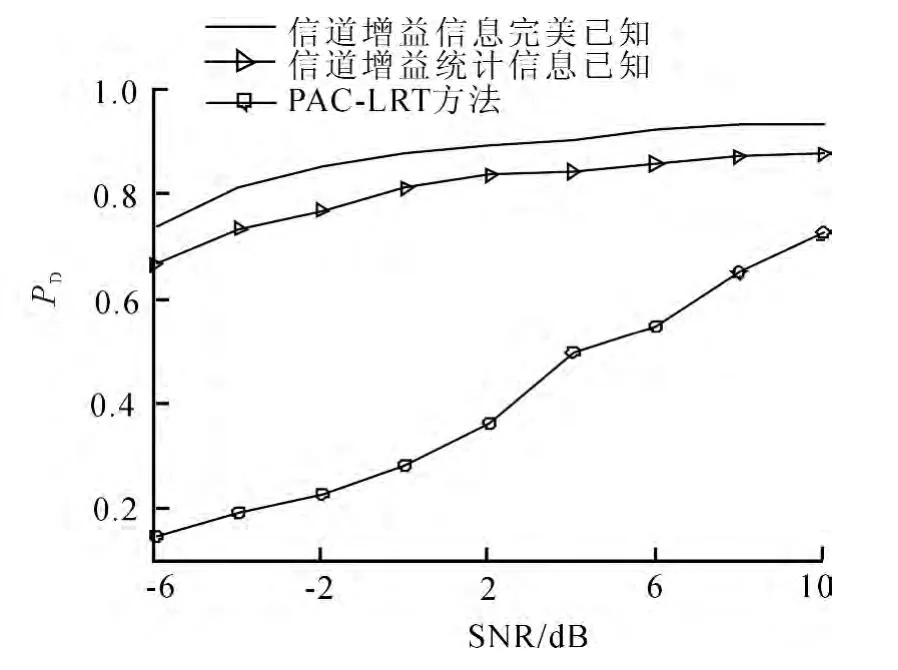
4 信噪比与检测概率之间的关系 （PF＝0．05，β＝10）Fig．4 Relationship between SNR and detection probability（PF ＝0．05，β＝10）

从仿真结果还可以看到，本文提出的信道增益统计信息已知时的局部发射功率约束部分相干检测融合方法的检测性能优于已有的基于并行网络拓扑结构的最优似然比方法（PAC-LRT）．

4 结 论

本文研究了局部传感器发射功率约束部分相干检测融合问题．在局部传感器发射功率约束条件下，建立了基于多址接入信道传输的多传感器分布式部分相干检测融合模型，该模型将融合中心处相位同步误差建模为服从吉洪诺夫（Tikhonov）概率分布的随机变量．利用偏移系数极大化理论优化融合系统的检测性能，得到了优化问题的闭合解．仿真结果表明：当环路信噪比大于等于10时，本文提出的局部发射功率约束部分相干检测融合方法能够显著提高多传感器检测融合系统的探测性能，在低信噪比条件下，其检测性能优于传统的基于并行网络拓扑结构的最优似然比方法．本文提出的新方法对于分布式远程预警目标探测系统的建立具有较高的理论参考价值．

［1］ PARK J，KIM E，KIM K．Large-signal Robustness of the Chair-varshney Fusion Rule under Generalized Gaussian Noises［J］．IEEE Sensors Journal，2010，10（9）：1438．

［2］ CHANG Q，CHENG B，CHEN，et al．Detection Performance Limits for Distributed Sensor Networks in the Presence of Nonideal Channels［J］．IEEE Transaction on Wireless Communications，2006，5（11）：3034．

［3］ LIN Y，CHEN B，SUTER B．Robust Binary Quantizers for Distributed Detection［J］．IEEE Transaction on Wireless Communications，2007，6（6）：2172．

［4］ CHEN B，JIANG R，KASETKASEM T，et al．Channel Aware Decision Fusion in Wireless Sensor Networks［J］．IEEE Transaction on Signal Processing，2004，52（12）：3454．

［5］ LIU K，SAYEED A M．Type-based Decentralized Detection in Wireless Sensor Networks［J］．IEEE Transaction on Signal Processing，2007，55（5）：1899．

［6］ LIN Y，CHEN B，TONG，L．Distributed Detection Over Multiple Access Channels［C］／／IEEE International Conference on Acoustics，Speech and Signal Processing，Honolulu，Hawaii，USA，2007，3：541．

［7］ LI F，JAMIE S．Decision Fusion over Noncoherent Fading Multi-access Channels［J］．IEEE Transaction on Signal Processing，2011，59（9）：4367．

［8］ CHAMBERLAND J F，VEERAVALLI V V ．Asymptotic Results for Decentralized Detection in Powerconstrained Wireless Sensor Networks［J］．IEEE Journal on Selected Areas in Communications，2004，22（6）：1007．

［9］ JAYWEERA S K．Large Sensor System Performance of Decentralized Detection in Noisy，Bandlimited Channels［C］／／IEEE 61st Vehicular Technology Conference （VTC）2005，Stockholm，Sweden，2005，2：1096．

［10］ ZHANG X，POOR H V，CHIANG M．Optimal Power Allocation for Distributed Detection over MIMO Channels in Wireless Sensor Networks［J］．IEEE Transaction on Signal Processing，2008，56（9）：4124．

［11］ WIMALAJEEWA T，JAYAWEERA S K．Optimal Power Scheduling for Correlated Data Fusion in Wireless Sensor Networks Via Constrained PSO［J］．IEEE Transaction on Wireless Communications，2008，7（9）：3608．

［12］ BERGER C R，WILLETT P，ZHOU S L，et al．Deflection Optimal Data Forwarding Over a Gaussian Multi-access Channel ［J］．IEEE Communications Letters，2007，11（1）：1．

［13］ LI W DAI H．Distributed Detection in Wireless Sensor Networks Using a Multiple Access Channel［J］IEEE Transaction on Signal Processing，2007，55（3）：822．

［14］ LI F ，JAMIE S．Optimal Strategies for Distributed Detection Over Multi-access Channels［C］／／IEEE International Conference on Acoustics，Speech and Signal Processing，Las Vegas，Nevada，USA，2008，3：2417．

［15］ XU Z，HUANG J，ZHANG Q F．New Method for Detection Fusion of Multiple-access Channel Based on Deflection Coefficient Maximization and NP Rule［J］． Journal of Systems Engineering and Electronics，2012，23（4）：612．

［16］ TEPEDELENLIOGLU C，DASARATHAN S．Distributed Detection over Gaussian Multiple Access Channels with Constant Modulus Signaling［J］．IEEE Transaction on Signal Processing，2011，59（6）：2875．

［17］ TIKONOV V I．The Effect of Noise on Phase-locked Oscillator Operation［J］．Automation and Remote Control，1959，20（9）：1160．

［18］ LAI K C，YANG Y L，JIA J J．Fusion of Decisions Transmitted over Flat Fading Channels Via Maximizing the Deflection Coefficient［J］．IEEE Transaction on Vehicular Technology，2010，59（7）：3634．

［19］ PICINBONO B．On Deflection as a Performance Criterion in Detection［J］．IEEE Transactions on Aerospace and Electronic Systems，1995，31（3）：1072．

［20］ GOODMAN L A．The Variance of the Product of k Random Variables［J］．Journal of the American Statistical Association，1962，57（297）：54．

［21］ GRADSHETYN I，Ryzhik I M．Table of Integrals，Series，and Products［M］．New York：Academic Press，4th edition，1983．

［22］ LUENBERGER D G．Linear and Nonlinear Programming［M］．New York：Springer，2008．