基于支持向量机的高速公路事件检测算法研究

周 洲，周林英，张立成，郝茹茹

（长安大学 信息工程学院，西安710064）

随着我国交通行业的快速发展，高速公路的大力建设在产生巨大的经济和社会效益的同时，也带来了不断加剧的交通拥挤以及不断增加的交通事故，这成为了高速公路日常运营管理中的一大难题.加强对高速公路事件检测算法的研究，提高高速公路事件检测的准确性，使管理部门能够对高速公路突发事件进行及时的处理和管控，最大限度的确保人员和车辆安全，提高高速公路的运营效率，充分发挥高速公路的优越性.

与传统的高速公路事件检测理论相比，SVM理论是以统计学习理论和结构风险最小化原理为基础的 学习模型，具有数学公式简洁、几何解释直观、泛化能力良好、能够有效避免局部最优解等优点.因此，利用SVM解决高速公路事件检测中普遍所存在的事件样本少、样本采集困难、检测效果不够理想等问题具有良好的应用［1－9］.

SVM可分为SVM，线性不可分SVM，非线性可分SVM三种类型.其核心思想是根据最大间隔原则求得最优分类面，从而判断任意输入所属的类别.线性不可分SVM需要优化惩罚参数C，对于非线性可分SVM，选择不同的核函数，可构成不同的支持向量机.目前，在分类问题方面常用的核函数主要有

1）多项式函数核函数：K（x，xj）＝ （（x·xi）＋coefo2，（coefo≥0，d）为阶数，d∈ N.特别地，当coef0＝0时为齐次多项式核函数.

2）高斯径向基核函数

＜k（x，xi）＝exp（－r‖x－xi‖2，r＞0

3）双曲线正切核函数

＜k（x，xi）＝tanh（r（x，xi）＋c），r＞0

1 基于SVM-AID的算法步骤和工作流程

基于支持向量的事件检测算法流程如图1所示.

① 数据准备阶段：包括交通数据选取、交通数据采集、数据优化处理等过程，并将数据分为训练数据集和测试数据集两部分.

②SVM核函数模型选择阶段：选择不同的SVM核函数模型，根据相对应的数据空间，利用特定的算法找出各个核函数模型所对应的最优参数，利用训练数据集分别对不同的SVM核函数模型进行训练.

③测试阶段：利用测试数据集对训练好的SVM模型进行测试，如果测试结果达到预先设定的条件，测试结束.否则，返回第②步，重新进行参数优化确定模型，并重新训练.

1.1 交通参数选择

选择上游检测点t、t－1、t－2、t－3、t－4时刻测得的流量、速度和占有率以及下游检测点t、t－1、t－2时刻测得的流量、速度和占有率作为SVM的输入，因此SVM有24个输入向量.用“＋1”标识有事件发生的特征向量，用“－1”标识无事件发生的特征向量.同时，定义当输出节点数为1个，输出值为“＋1”时，代表有事件状态，输出值为“－1”时，代表无事件状态.

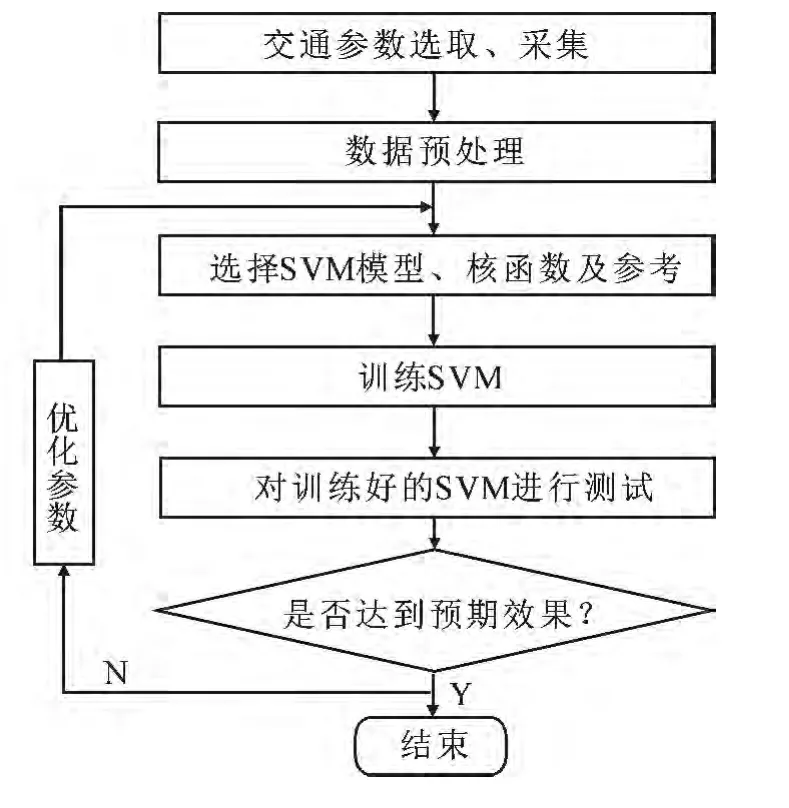
图1 基于SVM的事件检测算法工作步骤Fig.1 Main workflow of the incident detection algorithm based on SVM

1.2 交通数据来源

本文采用美国加利福尼亚州I－880数据库［10］作为交通数据来源，I－880数据库是美国Berkeley大学《Freeway Service Patrol Project》项目所采集的交通流数据.采集路段为美国加利福尼亚州Hayward的I－880高速公路，该路段全长9.41英里，车道数为3～5个，向北方向车道共埋设环形线圈18组，向南方向车道共埋设环形线圈17组.数据库的原始数据主要包括环形线圈数据集、浮动车数据集和交通事件数据集三部分.

1.3 模型及核函数的选择

不同的SVM模型、不同的核函数及其参数都会对算法的性能指标产生影响［11－12］，本文分别采用线性不可分SVM、齐次多项式核函数、高斯径向基核函数和双曲线正切核函数等4种不同的SVM模型对事件检测算法进行仿真分析，同时与经典的加利福尼亚算法进行对比.针对不同的核函数，需要对其相应的参数进行优化设定，本文采用网格搜索算法分别对多项式核函数的阶数，高斯径向基核函数中的参数，以及双曲线正切核函数中函数的参数和等参数进行优化，然后对给定的参数进行5－折交叉验证，通过反复实验，最终获得分类效果最好的一组参数.

2 算法仿真

设计4组实验，在每组实验中分别用基于线性不可分SVM、齐次多项式核函数、高斯径向基核函数、双曲线正切核函数等4种模型对事件检测算法进行仿真，不同算法中的参数寻优、模型训练、结果测试都采用台湾林智仁副教授提供的Libsvm工具箱［13］完成.其中，实验1（训练、测试数据均源自南向路段）和实验2（训练、测试数据均源自北向路段）用来验证算法的有效性.实验3（训练数据源自南向路段，测试数据源自北向路段）和实验4（训练数据源自北向路段，测试数据源自南向路段）用于验证算法的可移植性.各实验选取的模型及数据来源见表1.

表1 各实验选取的模型及数据Tab.1 Models and data of various experiments

2.1 仿真实验一

本实验用到的训练数据集、测试数据集均来自南向路段，利用表1中的数据对SVM模型进行训练和测试，用以验证算法的有效性.

1）线性不可分SVM在进行仿真实验之前首先利用2.3节提到的参数优化方法确定惩罚参数C的最优值.在对惩罚参数 进行优化的过程中，其取值范围的选择非常重要，选取不同的初始值，优化结果会产生较大差异，从而影响算法的最终分类效果.通过多次试验，选取不同的参数范围，最后得到线性不可分SVM的最优惩罚参数C＝0000795262.经过仿真，可以计算出相应的基于线性不可分SVM的事件检测算法的检测率为95%，误检率为0.52%，平均检测时间为103.26s.

2）采用齐次多项式作为核函数时，需要对惩罚参数C和阶数d进行优化设定.通过对不同初始值的设定检验，最终得到最优惩罚参数 ，再根据阶数取值的不同得到不同的检测率、误检率和平均检测时间.

3）利用高斯径向基作为核函数时，需要对惩罚参数C和核参数γ进行优化设定.通过对不同初始值的设定检验，得到一组预测率最优的参数（C，γ）＝（2048，1.19209289551e-007）.经过仿真，可以计算出采用高斯径向基核函数的事件检测算法的检测率为91%，误检率为0.53%，平均检测时间为100.55s.

4）利用双曲线正切作为核函数时，同样需要对惩罚参数C和核参数γ进行优化设定，通过对不同初始值的设定检验，得到一组最优的参数C＝（65536，9.31322574615e－010），经过仿真，可以计算出采用双曲线正切核函数的事件检测算法的检测率为94%，误检率为0.52%，平均检测时间为100.1s.

由以上实验可以得到基于线性不可分SVM、齐次多项式核函数、高斯径向基核函数、双曲线正切核函数情况下的算法有效性测试结果，并与经典的加利福尼亚算法进行对比，见表2.

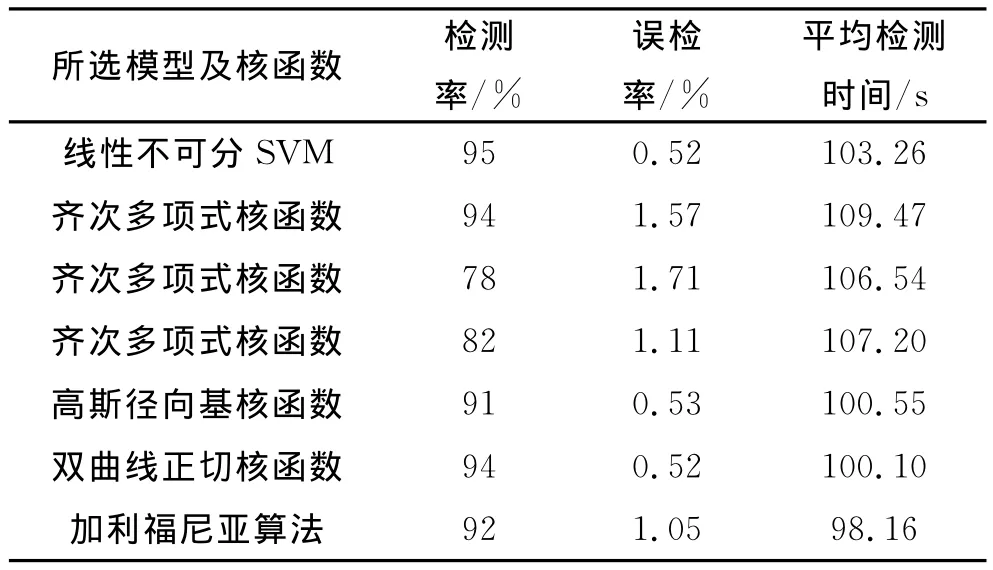
表2 实验1的有效性测试结果Tab.2 Simulation results of Experiment 1

2.2 仿真实验二

本实验用到的训练数据集、测试数据集均来自北向路段，利用表1中的数据对SVM模型进行训练和测试，该实验也用以验证算法的有效性.各模型的参数优化方法和实验1相同，分别获得线性不可分SVM的最优惩罚参数C＝0.013125，齐次多项式核函数的最优惩罚参数C＝9.53674316406e-07，高斯径向基核函数对应的最优惩罚参数C、核参数γ的最优参数组合为（C，γ）＝9.53674316406e－07，双曲线正切核函数的最优参数组合为 （C，γ）＝（131072，4.65661287308e－010）.

由以上结果可以计算得到在实验2的条件下基于线性不可分SVM、齐次多项式核函数、高斯径向基核函数、双曲线正切核函数情况下的算法有效性测试结果，并与经典的加利福尼亚算法进行对比，见表3.

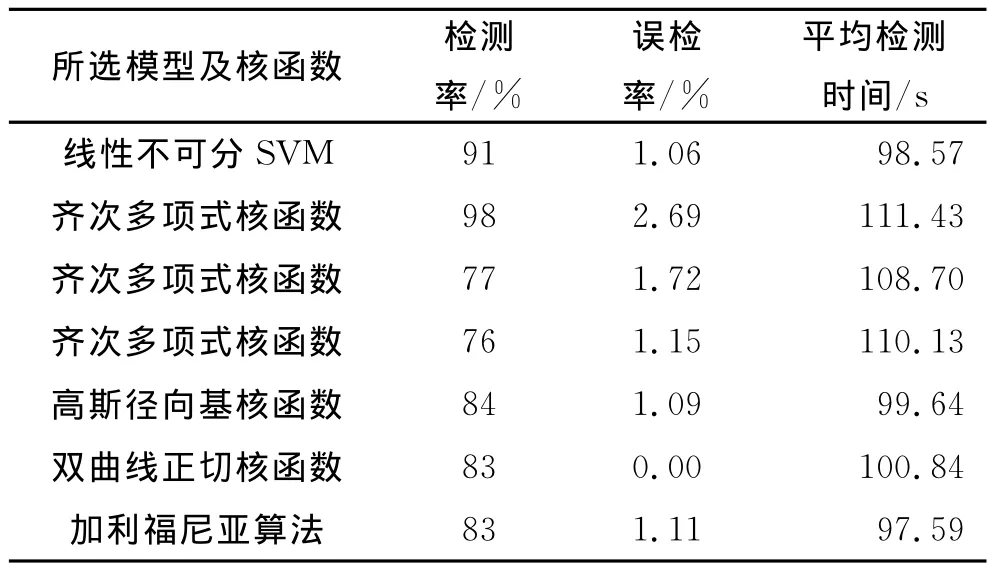
表3 实验2的有效性测试结果Tab.3 Simulation results of Experiment 2

2.3 仿真实验三

本实验用到的训练数据集、测试数据集来自不同的方向，用南向路段的数据（实验1的训练数据）作为训练数据集对各SVM模型进行训练，然后用北向路段的数据（实验2的测试数据）作为测试数据集对SVM进行算法测试，以此验证算法的可移植性.因为仿真实验3用到的训练数据集与实验1相同，所以各个模型相对应的最优参数与实验1相同.

由此可以计算得到在实验3的条件下基于线性不可分SVM、高斯径向基核函数、齐次多项式核函数、双曲线正切核函数情况下的算法可移植性测试结果，并与经典的加利福尼亚算法进行对比，见表4.

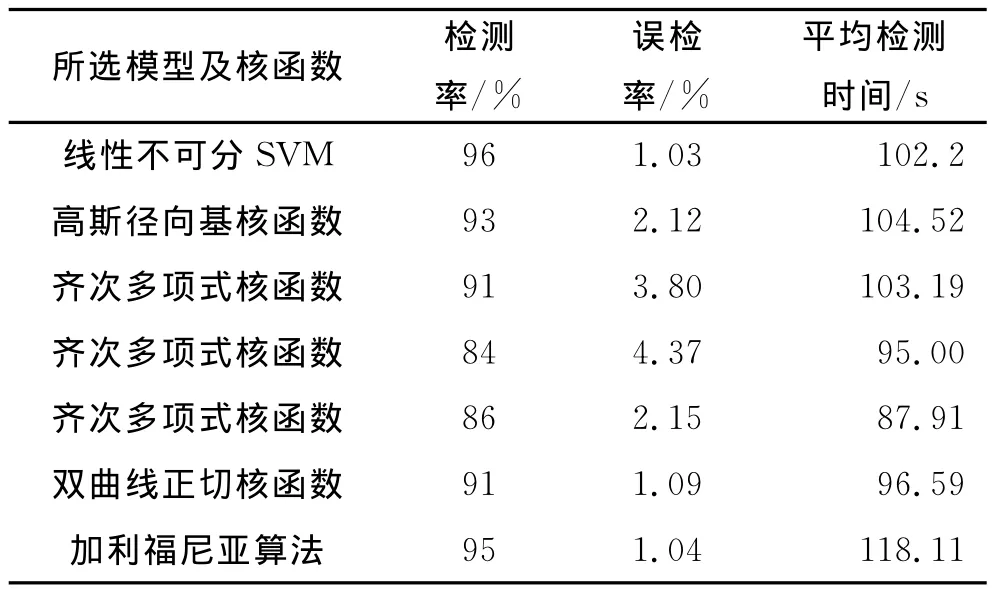
表4 实验3的可移植性测试结果Tab.4 Simulation results of Experiment 3

2.4 仿真实验四

本实验用到的训练数据集、测试数据集来自不同的方向，用北向路段的数据（实验2的训练数据）作为训练数据集对各SVM模型进行训练，然后用南向路段的数据（实验1的测试数据）作为测试数据集对SVM进行算法测试，以此验证算法的可移植性.因为仿真实验4用到的训练数据集与实验2相同，所以各个模型相对应的最优参数与实验2相同.由此可以计算得到在实验4的条件下基于线性不可分SVM、高斯径向基核函数、齐次多项式核函数、双曲线正切核函数情况下的算法可移植性测试结果，并与经典的加利福尼亚算法进行对比，见表5.

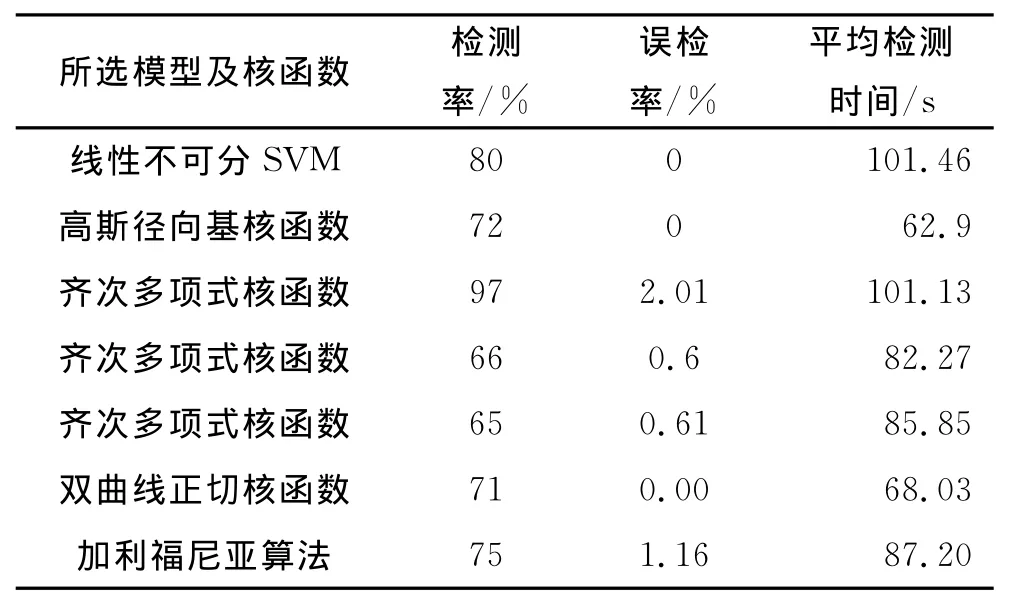
表5 实验4的可移植性测试结果Tab.5 Simulation results of Experiment 4

3 结果分析

3.1 有效性分析

从仿真实验1和实验2的数据可以看出1）从总体上看，基于齐次多项式核函数的模型与其他模型和算法相比，在检测率、误检率、平均检测时间等综合性能指标方面最差.

2）线性不可分SVM、高斯径向基核函数以及双曲正切核函数三种支持向量机模型的综合检测效果都要比加利福尼亚算法好.

3）由实验1和实验2两组实验可以看出，利用不同的核函数模型对同一数据集进行测试时，检测性能差异较大.因此，在实际应用中，需要根据数据集合的不同特点选择合适的核函数模型，才能得到最好的检测效果.

4）利用相同的SVM模型分别对南向路段数据集和北向路段数据集进行测试时，前者检测效果好于后者.由于南向路段数据集的交通事件大多是多车道事件，交通流波动较大，而北向路段数据集大多为单车道事件，交通流波动较小，因此，SVM模型针对交通流波动较大的事件具有更好的检测效果.

3.2 可移植性分析

从实验3和实验4的仿真结果可以看出

1）从总体上看，各种模型和算法在检测率、误检率、平均检测时间等综合性能指标方面，线性不可分SVM模型检测性能最好，基于齐次多项式核函数的模型检测性能最差.

2）由实验3和实验4两组实验可以看出，利用交通流波动较大的南向路段数据集对算法进行训练，用交通流波动较小的北向路段数据集进行算法测试时，检测效果较差.相反，利用交通流波动较小的北向路段数据集对算法进行训练，用交通流波动较大的南向路段数据集进行算法测试时，检测效果较好.因此，利用交通流波动较小的数据集训练出来的模型，算法的移植性较好.

4 结 论

1）利用SVM模型对高速公路事件进行检测时，不同的核函数及其参数对检测效果都有较大的影响.针对不同路段交通流的特点，选择合适的SVM模型并通过特定方法计算出其对应的最优参数，以此得到最佳的事件检测算法.

2）针对不同的高速公路交通事件，只要选择合适的SVM核函数模型，其算法的有效性和可移植性与经典的加利福尼亚算法相比，都有不同程度的提高.因此，基于SVM的高速公路事件检测算法具有良好的应用价值.

［1］ 崔志宾.基于支持向量机的交通事件检测建模与分析［D］.北京：北京交通大学，2008.CUI Zhi-bin.Modeling and Analysis of Automatic Incident Detection Based on Support Vector Machine［D］.Beijing：Beijing Jiaotong University，2008.（in Chinese）

［2］ 任双桥.支撑矢量机理论与应用研究［D］.长沙：国防科技大学，2006.REN Shuang－qiao Study on the Theory and Application of Support Vector Machines［D］.Changsha：National U－niversity of Defense Technology，2006.（in Chinese）

［3］ 杨志民，刘广利.不确定性支持向量机原理及应用［M］.北京：科学出版社，2007.YANG Zhi－min，LIU guang－li.Principle and Application of Uncertain Support Vector Machines［M］.Beijing：Science Press，2007.（in Chinese）

［4］ 王志龙.基于粗糙集理论与支持向量机的数据挖掘方法算法研究［D］.兰州：兰州大学，2007.WANG Zhi－long.Research on Data Mining Methods Based on Rough Sets Theory and Support Vector Machines［D］.Lanzhou：Lanzhou University，2007.（in Chinese）

［5］ 王朝勇.支持向量机若干算法研究及应用［D］.吉林：吉林大学，2008.WANG Chao－yong.Study of Some Support Vector Machine Algortithms and Their Applications［D］.Jilin：Jilin University，2008.（in Chinese）

［6］ 邓乃扬，田英杰.数据挖掘中的新方法——支持向量机［M］.北京：科学出版社，2004.DENG Nai－yang，TIAN ying－jie.A New Method for Data Mining—Support Vector Machine［M］.Beijing：Science Press，2004.

［7］ 彭新俊.支持向量机若干问题及应用研究［D］.上海：上海大学，2008.（in Chinese）PENG Xin－jun.Issues on and Applications of Support Vector Machines［D］.Shanghai：Shanghai University，2008.（in Chinese）

［8］ 周林英.基于支持向量机的高速公路事件检测算法［D］.西安：长安大学，2009.ZHOU Lin-ying.An Algorithm for Freeway Incidents Detection Based on Support Vector Machine.［D］.Xi’an：Chang’an University，2009.（in Chinese）

［9］ 周林英，朱斌，赵忠杰.基于支持向量机的高速公路事件检测算法［J］.系统仿真技术，2010，6（3）：224.ZHOU Lin－ying，ZHU bin，ZHAO zhong－jie.An Automatic Incident of Freeway Detection Algorithm Based on Support Vector Machine.［J］.System Simulation Technology，2010，6（3）：224.

［10］ Karl Petty.The Analysis Software for the FSP Project［EB／OL］.（1995－01－01）［2014－06－01］http：／／ipa.eecs.berkeley.edu／～pettyk／FSP／.

［11］ 王琪.基于神经网络和支持向量机的高速公路交通事件检测［D］.成都：西南交通大学，2006.WANG Qi.Traffic Incidents Detection Based on Neural Network and Support Vector Machine［D］.Chengdu：Southwest Jiaotong University，2006.（in Chinese）

［12］ 王鹏，朱小燕.基于RBF核的SVM的模型选择及其应用［J］.计算机工程与应用，2003，39（24）：72.WANG Peng.ZHU Xiao－yan.Model Selection of SVM with RBF Kernel and Its Application［J］.Computer Engineering and Applications，2003，39（24）：72.（in Chinese）

［13］ 张楠.关于支持向量机中的参数优化的研究［D］.西安：西北大学，2008.ZHANG Nan.Study of the Parameter Optimization in Support Vector Machines［D］.Xi’an：Northwest University，2008.（in Chinese）