电磁驱动飞板技术理论及试验研究
王叶中,黄正祥,祖旭东,肖强强,刘彦艳
(1.南京理工大学 智能弹药技术国防重点学科试验室,南京210094;2.63961部队,北京100021)
防护技术是提高武器系统生存能力的关键技术,传统的防护是基于装甲目标抗打击能力的被动防护。目前,随着脉冲功率源技术、脉冲强磁场技术、控制技术的发展,各国均将电磁发射技术作为未来主动防护技术的研究方向。相对于传统化学类发射装置,使用高储能脉冲功率源提供能量来发射的电磁驱动发射装置拥有更高的防护效率。主动电磁防护技术正是基于这些新的要求发展起来的[1-4]。
主动电磁防护技术主要是利用电能转化成电磁能并通过能量转换过程中产生的电磁力推动飞板,主动攻击来袭目标,造成来袭目标的毁坏或偏转,以达到防御的目的。圣路易法-德研究所于1986年首次完成了单级线圈电磁发射防护试验。结果表明,与爆炸反应装甲相比,达到同样的防护效果时电磁防护需发射的装甲板质量仅是爆炸反应装甲的1/3[5]。2001年进行的二维方向可控电磁发射的原理验证试验中发射装置实现二维方向可控的电磁发射,可以在轴线45°范围选择发射方向,误差小于0.5°[6]。美国陆军研究实验室对200~500g的平板进行了试验,可将560g的平板以280m/s的速度发射并成功地拦截了模拟来袭弹丸[7]。van de Voorde M J等人进行了电磁拦截装置拦截穿甲弹试验,试验结果显示,3kg的拦截弹以50m/s的速度拦截速度为1 337m/s的25mm口径穿甲弹,使得穿甲弹的穿甲深度减小为原来的60%[8]。Fedorov S V等研究表明,电磁驱动装置可将0.52kg的铝制圆盘发射到175m/s[9]。
电磁发射技术的研究在我国起步较晚,曹延杰教授对以同轴线圈发射原理为基础的电磁发射装置进行了研究,通过仿真分析了飞板在脉冲能量源放电时所受的电磁力和驱动线圈结构参数的变化对飞板所受电磁力的影响[10-14]。同轴线圈感应式电磁发射的理论及试验研究尚处于探索阶段,试验方案还不够完善,飞板结构的设计、飞板的精确控制、发射装置的模块化仍然有很多问题有待研究。
1 电磁驱动飞板运动过程分析
在电磁驱动飞板的运动过程中,由于电、磁能量转换以及磁、力耦合驱动飞板运动过程的相互影响,电磁驱动飞板运动过程的数学模型非常复杂,理论研究很困难。为便于分析研究,根据电磁驱动过程的具体工作情况,提出如下几点假设[15-16]:
①电磁驱动飞板发射过程中飞板不发生变形;
②放电回路的电参数近似不变;
③在电磁驱动飞板发射过程中,忽略空气阻力以及重力加速度;
④在考虑电路模型的时候,将发射装置电感参数变化看做一个只和飞板与发射线圈距离x变化相关的L(x)[11],相应地将含有耦合互感的电路模型简化为RLC串联脉冲放电电路。
1.1 电路模型
由电磁驱动飞板的发射模型可以发现,高压脉冲放电开关闭合后,放电回路中发射装置从脉冲电容器中获得一个强脉冲电流,整个放电回路可以简化为RLC串联电路,如图1所示。

图1 电磁发射等效电路
图1 电路中,设电容器、脉冲放电开关都为理想元件,R为发射线圈电阻和整个回路电缆电阻,L为回路电缆的自感和扁平线圈的自感,M为发射线圈与飞板的互感,L(x)为自感L和互感M的总和,U(t)为脉冲电容器的充电电压,I(t)为回路的脉冲放电电流。由RLC二阶电路的零输入响应,对图1建立电路方程:
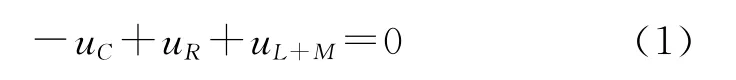

脉冲放电电流I(t)可表示为

式中:

1.2 飞板发射阶段运动模型
由于飞板与发射线圈距离相对较近,能量能有效储存在飞板和线圈间的互感上,互感的变化导致能量变化驱动飞板[17]。
电感元件是一种动态元件,可以将电路中的能量以磁场能量的形式存储在磁场中,因此,线性电感元件吸收的功率为

式是:i为通过电感元件的电流。
从0到t时刻电感储存的磁场能量为

而主动电磁发射装置的电感:
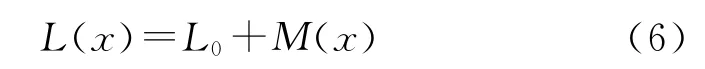
由虚位移原理可知线圈相互作用力为

通过牛顿定律可知:

式中:m为飞板的质量。
综合式(3)、式(5)、式(8)得到飞板的运动方程:

通过电感分析和运动方程可以求解互感M、位移x和时间t之间的关系。
1.3 电感分析
在整个脉冲放电回路中,发射线圈电感L(x)只与飞板与发射线圈距离x变化相关。当飞板与发射线圈距离x相对较远时,L(x)的大小相当于发射线圈的自感。由于L(x)大小的变化只与飞板与发射线圈距离x变化相关,而距离x的变化只与发射线圈与飞板互感M有关,因此距离x的变化只与发射线圈和飞板互感M有关。L(x)的变化相当于发射线圈与飞板之间互感M的变化。所以L(x)可近似为发射线圈的自感L和发射线圈与飞板之间互感M的总和[11]。
1.3.1 发射线圈的自感
1)矩形截面圆环的自感。
线圈电感的计算中一般忽略线圈的螺旋性,并且线圈被视为自闭合的平面线圈组合。这样线圈的电感计算误差较小,线圈的电感计算误差可以忽略,因此线圈的自感计算如下:
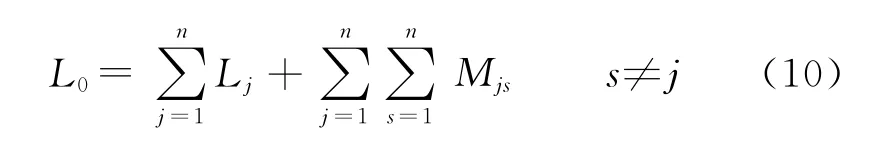
式中:Lj为单个圆环自感,Mjs为各圆环间互感,n为线圈匝数。
2)长度相同的矩形截面同心圆环互感。
图2为长度相同矩形截面圆环结构示意图,图中,r″是圆环半径,a和r′是导体横截面轴向和径向尺寸。
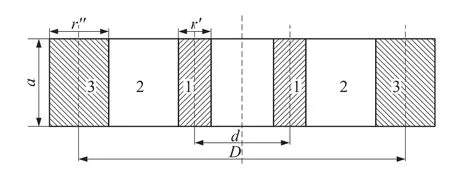
图2 长度相同矩形截面同心圆环

式中:L123,L12,L23分别为由相应的圆环1、2和3,1和2,2和3组成的圆环的自感;L2为长度为a、直径为[D+d-(r″-r′)]/2的虚设圆环2的自感。
1.3.2 飞板的自感
处在瞬变磁场的飞板产生感应涡电流,脉冲电流作用在发射线圈时,发射线圈周围产生瞬变磁场,瞬变磁场中的飞板中会感应出涡电流,涡电流可看成无数个载流圆环,而每个圆环的涡电流(径向涡电流)是不同的,且同一个圆环上涡电流(即轴向涡电流)也是不同的,这些涡电流激发的磁场与发射线圈周围产生的瞬变磁场方向相反。导体中涡电流分布的计算极其复杂,现简化成计算相对简单、有确切参数的问题。假设导体存在确定尺寸的圆环,当在圆环上加载均匀电流时,若该电流通过圆环截面的总电流与导体中感应的涡电流大小相等,且这个圆环的阻抗近似等于导体的有效阻抗,导体的电参数就可以用此圆环的电参数来代替,在实际计算中产生可接受的误差。根据Loos H R的涡电流模型假设,飞板可近似为一个径向半径等于线圈半径,轴向厚度为趋肤深度的确切几何尺寸的环域,当环域的截面内通过与涡电流相等的电流时,环域的实际自感应与飞板的自感相等。
1.3.3 发射线圈与飞板的互感
1)同轴圆环的互感[18]。
图3为同轴圆环相互位置示意图,在图3中,半径R1、R2的圆环同轴放置,圆环所在的平面相互平行。设两圆环平面间距为x。在两圆环上任一点处线元分别为dl1,dl2,则
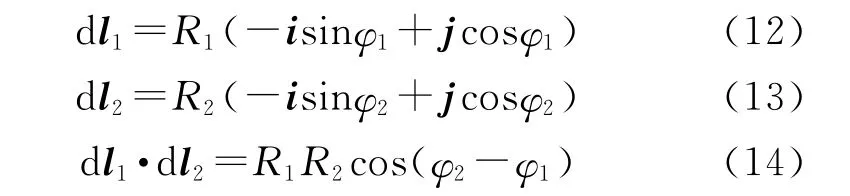
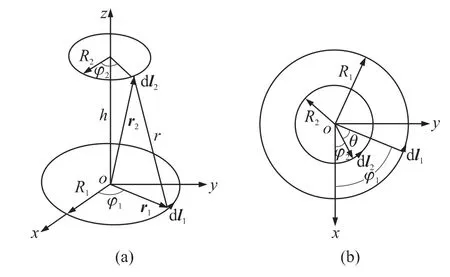
图3 同轴圆环之间的互感
两圆环上任意两点间的距离:

任意两单匝细线回路的互感:
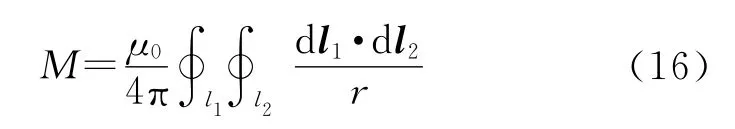
令θ=φ2-φ1,代入简化得:

对式(17)进行变换,令θ=π-2α,k=,则有

及

因此,

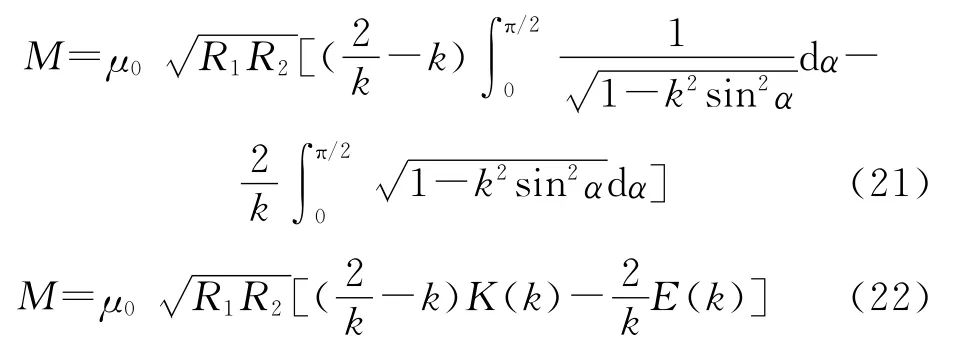
当k值接近于1时,上述电感求解计算式因为相邻k值对应的E(k)值变化比较大,在它们之间进行插值精度比较低,因此需要变通为以k1为模数的第一类和第二类全椭圆积分,宜用:

2)矩形截面同轴线圈的互感[19]。
矩形截面同轴线圈如图4所示。
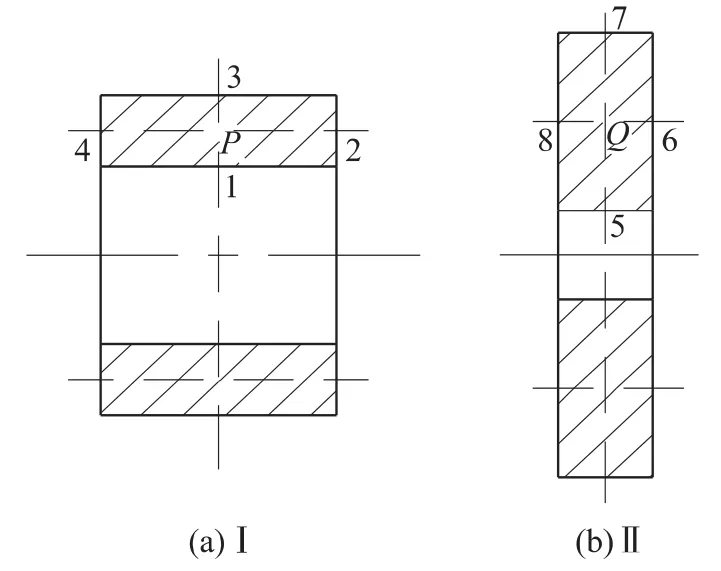
图4 矩形截面同轴线圈的互感
利用泰勒级数法把2个矩形截面线圈的互感表示为10个同轴圆环回路的互感,在图中显示标记回路,则

3)线圈和飞板的互感。

式中:n为飞板的匝数,w为扁平线圈的匝数,Mjs为第j个和第s个线圈之间的互感。
通过Matlab数值迭代的方法拟合类似于确定飞板与发射线圈互感M(x)和距离x的关系,如图5所示。
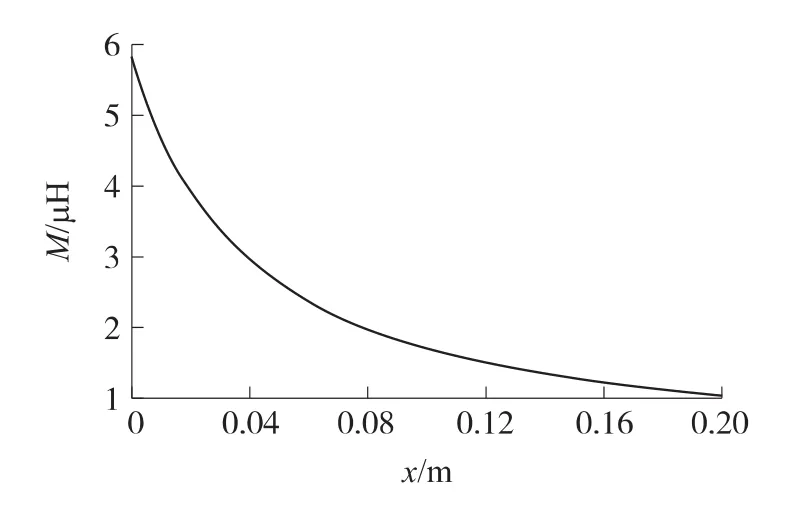
图5 飞板与发射线圈互感M(x)和距离x的关系
当两同轴线圈的半径确定后,线圈间互感的变化和两线圈距离呈指数变化关系,因此,飞板与发射线圈互感M(x)和距离x的关系为指数函数:

式中:M0相当于x=0时飞板与发射线圈间的互感,γ是一个关于距离x变化的感应率比值。
1.4 电阻分析
1)发射线圈电阻。
电磁飞板的发射线圈为阿基米德螺旋线圈。设线圈宽为b,厚为h。
取极坐标,则发射线圈导线的中心线的参数方程为
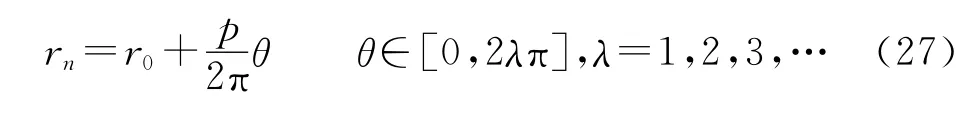
式中:λ为发射线圈的圈数;r0为圆心到线圈第一匝起点中间位置的距离,即初始半径;p为线圈间距。
为便于计算,将阿基米德螺旋线圈的长度计算简化为间距相等的同心圆组成的线圈的长度计算,如图6所示。

图6 简化后的同心圆线圈
任一同心圆中心线的半径为

式中:ζ为同心圆的圈数;rζ为第ζ匝圆环线圈半径。则发射线圈的总长l为

发射线圈的电阻R为[20]

式中:ρ为导线电阻率,S为发射线圈的截面积,f为临近效应系数,δ为趋肤深度。
2)趋肤深度。
RLC非振荡发电过程中,电流近似正弦增长,则发射线圈中电流的趋肤深度为[21]

式中:μ0为真空磁导率,μ0=4π×10-7。
2 主动电磁发射试验结果及分析
主动电磁驱动飞板基本原理是通过充电设备对脉冲电容器长时间充电,把电能存储在电容器内,设定放电开关击穿电压,当脉冲电容器充电电压达到放电开关击穿电压时,脉冲电容器、放电开关、发射装置的回路中产生脉冲电流,发射装置周围产生瞬态的强磁场,飞板内产生巨大的感应涡电流,飞板受到电磁力作用发射。试验装置和电磁飞板发射装置如图7、图8所示。

图7 试验的储能系统、充电系统和放电开关

图8 主动电磁发射装置(发射线圈、底座、飞板)
为了直观查看主动电磁飞板试验各装置的连接方式,电磁驱动飞板的试验系统如图9所示。

图9 电磁驱动飞板的试验系统
由于主动电磁发射的整个电路中的连接方式对于发射能量损耗比例较高,因此在整个分析过程中需要将整个电路中电缆的电阻、电感,连接电容器的铝条的电阻、电感都要计算在内,因此试验时首先测量发射电路中各电参数,电缆、铝条、发射线圈的电参数如表1所示。
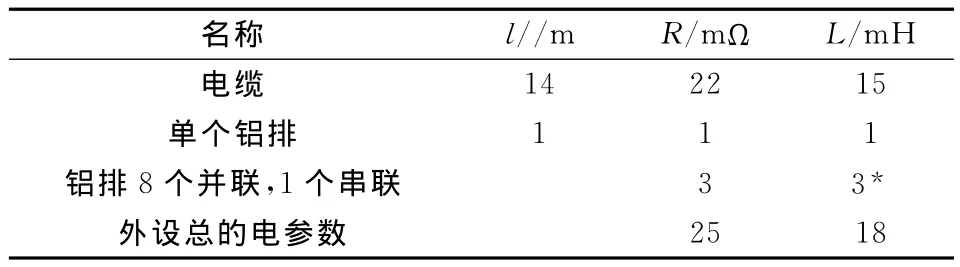
表1 外设装置电参数
电磁飞板发射的飞板飞行状态以及运动轨迹如图10所示。

图10 发射过程中飞板运动轨迹
根据图10中飞板的发射过程可知,飞板在发射时产生巨大的火光,飞板大约在离发射线圈高度为0.2m时达到最大速度,最大速度约为45m/s,且飞板在发射过程到离发射线圈2m处时,仍能保持一定的姿态。
发射后发射装置及飞板的形态如图11所示。由图11可以发现,发射线圈发生了塑性变形,发射底座没有受到损坏,飞板局部发生塑性变形。发射过程中伴随着强烈的火光。线圈经过3次脉冲放电试验后才发生塑性变形,说明当几十kA的电流作用在发射线圈上时,发射线圈有一定的使用寿命。并且在一次脉冲放电试验后发现发射线圈温度上升,这说明涡电流引起了一定的损耗。由于在发射上方4m处设置了混凝土的防护装置,飞板与之碰撞后导致边角变形,证明电磁驱动的飞板有较大的动能。

图11 发射后的发射装置
图12 是理论计算脉冲电流与实验测量脉冲电流的变化关系。从图中可以发现,在脉冲放电的第一个周期内,理论计算曲线与试验测量曲线重合较好,但理论计算的放电周期比试验测量的放电周期略大。理论计算的脉冲电流峰值与实际测量的脉冲电流峰值基本吻合,这是由于理论计算的电流曲线中各电参数未发生变化;而当第二个脉冲电流放电周期时理论计算曲线与试验测量曲线就开始产生一定的误差,这是因为飞板与发射线圈距离的变化以及飞板运动的状态不是平动,导致发射装置互感发生变化。实际试验的发射线圈温度上升导致发射线圈的电阻产生变化,造成理论计算的脉冲放电周期以及脉冲电流峰值都要比实际测量值大。当脉冲放电1ms以后,飞板早已离开发射线圈,飞板与发射线圈之间的互感值为零,飞板不再受到电磁力的作用,此振荡电流的能量将最终被回路中的电阻吸收以及被发射线圈的发热所损耗。

图12 理论计算与实验测量的脉冲电流变化关系
表2为实验测量参数。表中,Imax为峰值电流,Fmax为峰值电磁力,v为飞板速度。

表2 试验电容器C=80μF,U=28.7kV时测量参数
由表2可以得到当电容器放电电压U=28.7kV时,第一个脉冲电流周期内理论与试验测量的峰值电流分别为59.3kA和61kA,两者相对误差为2.78%,理论计算得到的飞板最终速度为54m/s,高速摄像拍摄的飞板最终速度为45m/s,两者的相对误差约为16.6%。由于理论计算中没有考虑飞板自身的质量以及飞板在运动中受到的空气阻力,因此,理论计算比测量的速度略大。
3 结论
①通过对主动电磁发射过程进行假设,将电磁发射过程的电路模型简化为RLC串联电路,并根据Loos H R的涡电流模型简化的基本设想以及确定线圈间互感变换规律共同拟合出飞板与发射线圈之间互感变化规律的数学模型。
②通过对放电回路中其它电参数的计算,特别是发射线圈电阻的计算,得到整个放电回路的脉冲电流,利用电、磁能量转换,牛顿定律和虚位移原理共同建立了飞板发射阶段的理论运动模型。
③通过高速摄像观察电磁驱动飞板的发射过程,将测量结果与理论计算模型相互比较,试验证明了电磁驱动飞板物理模型的可行性。
[1]王凤英.装甲防护技术的发展[J].测量技术学报,2002,16(2):144-147.WANG Feng-ying.The development of armor fence[J].Journal of Testand Measurement Technology,2002,16(2):144-147.(in Chinese)
[2]李向东,钱建平,曹兵,等.弹药概论[M].北京:国防工业出版社,2004.LI Xiang-dong,QIAN Jian-ping,CAO Bing,et al.Ammunition introduction[M].Beijing:National Defense Industry Press,2004.(in Chinese)
[3]WILLIAM F.Development of hypervelocity electromagnetic launchers[J].Impact Engng,1987,5(1-4):671-679.
[4]MARK H.Electromagnetic launch technology:the pomise and the problems[J].IEEE Transactions on Magnetics,1989,25(1):17-19.
[5]胡金锁,李治源,王莹.坦克装甲车辆电磁装甲技术与研究现状[J].现代兵器,2002(6):34-36.HU Jin-suo,LI Zhi-yuan,WANG Ying.Technology and research status of electromagnetic armored of tanks and armored vehicles[J].Modern Weaponiy,2002(6):34-36.(in Chinese)
[6]STERZELMEIER K,BROMMER V,SINNIGER L.Active armor protection-conception and design of steerable launcher systems fed by modular pulsed-power supply units[J].IEEE Transactions on Magnetics,2001,37(1):238-241.
[7]宁俊生,孙葆森,黄立松,等.电(磁)装甲研究现状及发展趋势[J].兵器材料科学与工程,2001,24(4):54-57.NING Jun-sheng,SUN Bao-sen,HUANG Li-song.Developmental tendency and present level of research on electromagnetic armor[J].Ordnance Material Science and Engineering,2001,24(4):54-57.(in Chinese)
[8]Van de VOORDE M J,BOESCHOTEN R.The use of electric power in active armour application[C]//Proceedings of the 22th International Symposium on Ballistic.Vancouver,Canada:IBC,2005:925-932.
[9]FEDOROV S V,BABKIN A V,LADOV S V.Theoretical analysis of system of electro-magnetic acceleration of metal plates[C]//Proceeding of the 25th International Symposium on Ballistic.Beijing,China:IBC,2010:638-646.
[10]金洪波,曹延杰,贺英政,等.扁平线圈电磁发射器优化设计[J].兵工自动化,2009,28(5):46-49.JIN Hong-bo,CAO Yan-jie,HE Ying-zheng,et al.Optimal design for flat coin electromagnetic launcher[J].Ordnance Industry Automation,2009,28(5):46-49.(in Chinese)
[11]WANG Hui-jin,HUANG Yong-fang,LI Rui-feng,et al.Structural optimization of electromagnetic launcher in active electromagnetic armor[J].IEEE Transactions on Plasma Scinece,2011,39(1):487-491.
[12]王成学,曹延杰,邹本贵.主动电磁装甲拦截弹发射过程研究[J].电光与控制,2009,16(8):93-96.WANG Cheng-xue,CAO Yan-jie,ZOU Ben-gui.Research on launching process of interception projectile in active electromagnetic armor[J].Electronics Optics & Control,2009,16(8):93-96.(in Chinese)
[13]CAO Yan-jie,WANG Cheng-xue,WANG Hui-jin,et al.Simulation of electromagnetic launcher of active electromagnetic armor[J].IEEE Transations on Electromagnetics,2008,44(1):1-4.
[14]WANG Cheng-xue,CAO Yan-jie,ZOU Ben-gui,et al.Research on EM launcher of active EM armor with field-circuit coupled method[J].IIEEE Transactions on Plasma Scinece,2011,39(1):481-486.
[15]胡金锁.电磁装甲技术原理及其有限元分析[M].北京:兵器工业出版社,2005.HU Jin-suo.Electromagnetic armor technology principle and finite element analysis[M].Beijing:Ordance Industry Press,2005.(in Chinese)
[16]NOVAC B M,SMITH I R,SENIOR P,et al.Can the efficiency of an electrostatic to kinetic energy conversion process exceed 50%?[C]//11th IEEE International Pulsed Power Conference.Baltimore,MD,USA:IEEE,1997:1 139-1 143.
[17]卡兰塔罗夫,采伊特林.电感计算手册[M].第1版.陈汤铭,刘保安,罗应立,张奕黄译.北京:机械工业出版社,1992.
[18]STUETZER O M.Theory of small compressed magnetic flux current amplifiers[M].USA:Sandia Laboratories,1979.
[19]LOOS H R.Wirkungsweise and berechung von mebwertaufunhmern auf wirbelstromhasis zur beruhungsfreien wegmessung [M].Munchen:Technisches Messn Atm,1976.
[20]KNOEPFEL H.Pulsed high magnetic fields[M].Amsterdam:North-Holland Publishing Company,1970.
[21]赵博,张洪亮.Ansoft 12在工程电磁场中的应用[M].北京:中国水利出版社,2010.ZHAO Bo,ZHANG Hong-liang.The application of Ansoft 12 in electromagnetic field engineering[M].Beijing:China Water Conservancy Press,2010.(in Chinese)

