导弹对面积目标射击效能的智能优化算法

汪民乐，房茂燕

（第二炮兵工程大学 理学院，西安710025）

对面积目标射击效能优化问题是导弹作战效能分析中一个经典而复杂的问题，其本质是导弹瞄准点的优化选择［1－4］。由于目标函数的复杂性，对面积目标射击导弹瞄准点的优化是典型的非线性多峰函数优化问题。对该问题，基于爬山法（Climbing）的传统求解算法效率低下，且通常只能获得次优解，因而不能充分发挥导弹的毁伤效能，也不利于提高作战指挥决策的效率。在导弹射击效能分析实践中，为使问题简化，常见的做法是将面积目标形状近似为规则的几何形状，利用已有的特殊函数（如：拉普拉斯函数）来简化瞄准点优化问题的目标函数，以降低问题求解的难度和计算量。但这种对目标形状的近似势必带来求解精度的下降，直接影响导弹瞄准点优化选择的效果，而且即便是简化后的问题，其求解复杂性依然存在，这已为大量实际问题所证明。遗传算法作为一种仿生类智能优化算法［5－8］，采用群体搜索策略，由于其搜索过程的隐并行性，对导弹瞄准点优化这类复杂非线性优化问题具有较高的求解效率，同时也具有较高的全局收敛性。遗传算法的求解过程还不依赖于问题本身，主要表现在对目标函数的复杂性不敏感，甚至不要求有目标函数表达式［9－10］，而这一特性尤其适合于导弹瞄准点优化这类具有复杂目标函数的问题。此外，用遗传算法求解对面积目标射击导弹瞄准点优化问题，无须对面积目标形状进行近似，即适应于任意形状面积目标，而对任意形状面积目标瞄准点优化问题至今仍是射击效能分析中的难点。因此，用遗传算法求解导弹瞄准点优化问题具有传统算法无可比拟的突出优点。

1 对面积目标射击效能优化模型

在面积目标价值分布不均匀的情况下，对面积目标射击效能优化问题是一个多目标优化问题，需要考虑的目标有3个：objective 1，平均毁伤面积尽量大；objective 2，平均毁伤价值尽量大；objective 3，脱靶面积尽量小。

设面积目标所占区域为SA，对该目标发射N发导弹，试决定N发导弹的瞄准点坐标（xi，yi）（i＝1，2，…，N），以使总的射击效能最优，即

式中：f1，f2，f3分别表示objective 1，objective 2，objective 3的目标函数；f为目标函数向量。建立对面积目标射击效能多目标优化模型的关键是3个目标函数表达式的构造。以下分别给出各目标函数表达式。

1）objective 1的目标函数表达式。

objective 1的目标函数为：maxf1＝M［Sh］，式中：Sh为N枚导弹总的杀伤面积。M［Sh］的计算需分2种情形进行。

①当N枚导弹射击相互独立时：

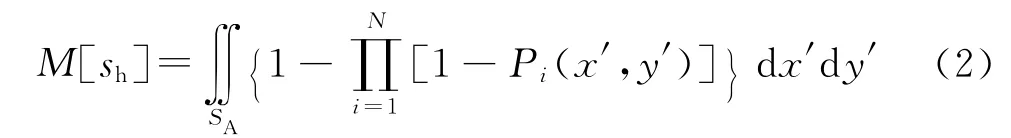
式中：（x′，y′）为SA上任一点坐标，Pi（x′，y′）为第i枚导弹对以（x′，y′）为中心的面积元的杀伤概率：

式中：Gi（x－x′，y－y′）为第i枚弹作用下（x′，y′）的依坐标毁伤律，当各枚导弹威力相同时，依坐标毁伤律可统一记为G（x－x′，y－y′）；φi（x，y，xi，yi）为第i枚导弹在以（xi，yi）为瞄准点的情况下弹着点分布律。

在给定（xi，yi）（i＝1，2，…，N）时，Pi（x′，y′）及M［Sh］的计算需采用高维数值积分方法。

②当N枚导弹射击相关时：

式中：（xg，yg）表示N枚导弹的集体误差，φg（xg，yg）为集体误差分布密度函数，Pi（x′，y′，xg，yg）为在固定的集体误差下第i枚导弹对以（x′，y′）为中心的面积元的杀伤概率，则

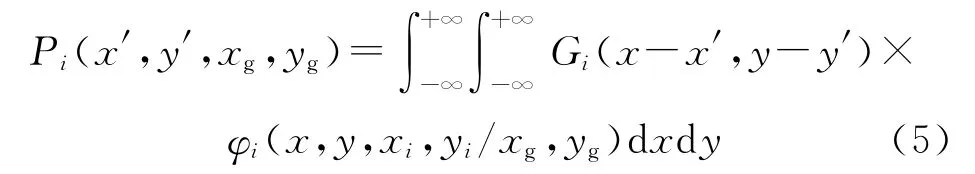
式中：φi（x，y，xi，yi／xg，yg）表示在固定的集体误差（xg，yg）下，第i枚导弹在以（xi，yi）为瞄准点时弹着点的条件分布密度函数。

2）objective 2的目标函数表达式。

objective 2的目标函数表示达式：maxf2＝M［Vh］，其中，Vh为N枚导弹总的毁伤价值。

完全类似于objectivet 1目标函数表达式的建立过程，同样分2种情形计算在瞄准点坐标为（xi，yi）（i＝1，2，…，N）时的M［Vh］。

①当N枚导弹射击相互独立时：

式中：V（x′，y′）为面积目标的价值密度函数。

②当N枚导弹射击相关时：

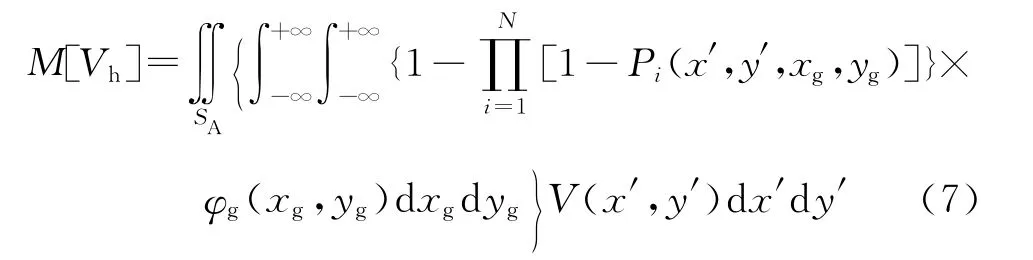
3）objective 3的目标函数表达式。

以各枚导弹瞄准点距面积目标中心距离的和作为objective 3的度量，则目标函数形式为

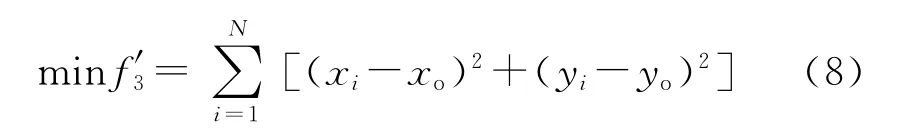
为统一于式（1）的形式，将式（8）等价为下列形式：

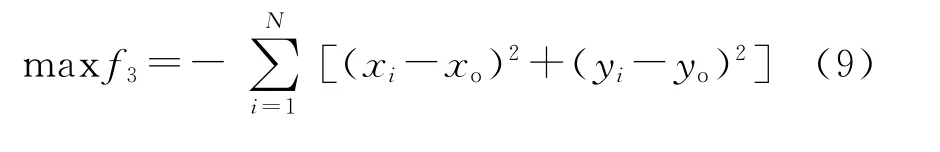
式中：（xo，yo）为面积目标中心坐标。

2 对面积目标射击效能的遗传优化算法设计

由于多目标遗传优化算法在求解多目标优化模型上的独特优势，以及面积目标射击效能多目标优化模型的复杂性，适宜采用多目标遗传优化算法对其求解。在求解时，有2种策略：①直接求解，即同时考虑3个目标，此时为多目标无约束优化；②将objective 3化为约束，从而将问题简化为二目标的优化，约束形式为

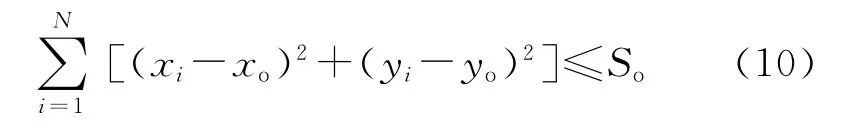
式中：So为某一正值。此约束的数学意义是把（xi，yi）（i＝1，2，…，N）局限在R2N中的一个超球内。

由此可见，无论采取何种策略，Objective 1和Objective 2都必须同时被考虑，这是因为二者表达的目的不同。Objective 1的目的是使杀伤范围尽量大，以造成广泛的心理压力，最大程度地削弱敌方士气；objective 2的目的是最大程度地摧毁敌方军事、经济实力，获取最高的作战效费比。可以形象地说，objective 1的效应体现在横向，而objective 2的效应体现在纵深。从瞄准点选择的角度来看，objective 1要求弹着点稀疏，以使重复杀伤尽量小，而objective 2要求弹着点置于高价值区域，objective 3则要求弹着点集中于目标中心。必须指出的是，当目标价值分布均匀时，objective 1与objective 2等价。以下将采用第2种求解策略，即简化为二目标优化问题。

2.1 编码方案

在利用遗传算法求解问题时，最先解决的应该是编码问题，即如何将问题的解转化为染色体，在对面积目标的攻击决策过程中主要涉及到目标瞄准点的坐标。图1所示阴影部分表示面积目标Si，对Si的发射弹数为ni，瞄准点坐标记为（）（j＝1，2，…，ni），瞄准点应置于Si上以减小脱靶面积。

图1 面积目标示意图

根据Si幅员可得：

为减小染色体编码长度，采用实数编码。每个染色体由ni个基因段构成，每个基因段包含2个基因，分别表示瞄准点横坐标和纵坐标。因此，染色体总长度为2ni，整个染色体编码代表子模型的一个解，如图2所示。

图2 染色体示例

2.2 适应度函数的计算

针对不同的射击情形，在不计杀伤积累的条件下，建立不同的适应度函数。

①各枚导弹的射击相互独立，且弹着点随机散布。

此种情形见于各枚导弹由不同平台发射，或虽由同一平台发射，但每次射击均重新瞄准。

设第j枚导弹弹着点坐标的标准差为σxj，σyj，不计系统误差，弹着点坐标联合概率密度函数为

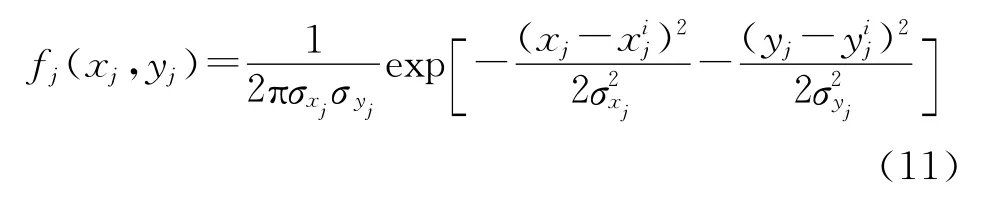
设（x′，y′）为Si上任一点，则该点被第j枚导弹杀伤的概率为

式中：Rj为第j枚导弹的杀伤半径。

由于ni枚导弹射击相互独立，则（x′，y′）至少被一枚导弹杀伤的概率为

设d（x′，y′）表示（x′，y′）处目标价值密度，则ni枚导弹对面积目标Si的平均杀伤价值为

在式（14）中令d（x′，y′）＝1，则此时将得到平均杀伤面积。

对于任一个体X，以平均杀伤面积作为其第一适应度f1（X），以平均杀伤价值作为其第二适应度f2（X），这样，任一个体X均 对应一个适应度向量f（X）：

②各枚导弹射击相关，且弹着点随机散布。

此种情形见于各枚导弹由同一平台齐射或连射。

设射击随机误差为2组误差型，且集体随机误差为（xG，yG），其分布密度为fG（xG，yG），在（xG，yG）一定的情况下，各枚导弹射击相互独立。设第j枚导弹弹着点坐标在固定随机误差下的条件密度为fj（xj，yj／xG，yG），类似于式（13）得ni枚导弹在固定的（xG，yG）下杀伤Si上任一点（x′，y′）的概率为

式中：

考虑到（xG，yG）的随机性，由全概率公式得ni枚广义弹对（x′，y′）的杀伤概率为

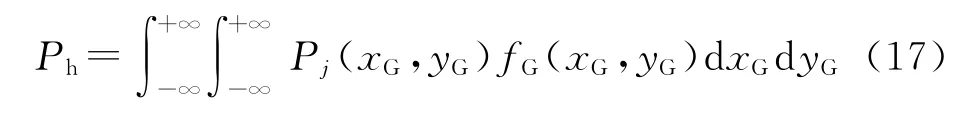
至此，完全类似于式（14），可以得到任意个体X的适应度向量f（X）。

③ni枚导弹部分相关且弹着点随机散布。

所谓部分相关是指ni枚导弹可以划分为若干类，每一类导弹射击相关，但各类之间射击相互独立。此种情形见于多个平台射击，每一平台齐射或连射若干枚，或由同一平台进行多轮射击，每一轮射击齐射或连射若干枚导弹且各轮射击均重新瞄准。

不失一般性，设ni枚导弹可划分为q个相关类，第k类包括nik枚导弹，显然

首先由②中的方法求出第k个相关类中导弹对Si上任一点（x′，y′）的杀伤概率Phk（k＝1，2，…，q），再由①中方法求出q个相关类对（x′，y′）的杀伤概率Ph：

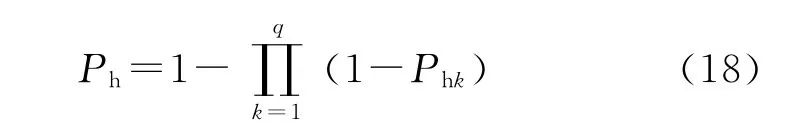
由Ph，采用与①、②中完全类似的方法，即可得到任一个体X的适应度向量f（X）。

④不考虑弹着点散布，即认为各弹落点无飘移。

此种情形下选择最优瞄准点实际上是选择最优“成爆点”，即导弹应成爆于此；至于散布问题，应在发射或投掷过程中加以控制，力求准确命中预定瞄准点。事实上，投射误差是无法预测的，这主要是由于大量随机误差的影响。指出成爆点已经为攻击行动指明了方向，达到了支持战前决策的目的，这也正是本文研究与以往文献的一个不同之处。

精确制导技术的发展也为这种选取瞄准点的方法提供了有力支持。例如：射程长达2 000km的战斧式巡航导弹误差仅10m左右，其它短程导弹误差更小，且更易控制其瞄准、命中过程。用选择“成爆点”代替选择瞄准点的思想可避免大量繁杂而效益不大的推导、计算，大大节省计算时间，从而向瞄准点选择的快速化甚至实时化迈进一大步。

在无飘移情形下计算个体适应度可采用目标分块法，即通过加网格将目标划分为许多小矩形块，根据小矩形块中心坐标以及各枚导弹预定弹着点坐标对小矩形块作杀伤判断，并分别作杀伤价值和杀伤面积累加，即可得到个体的适应度向量f（X）。

2.3 适应度函数的再设计

根据瞄准点选择多目标优化的需要，对适应度函数进行再设计，该适应度函数由2个函数构成，定义如下。

定义1 极值性适应度函数。

对于任意个体X，有一个适应度向量f（X）与之对应，以该向量的长度作为个体X的极值性适应度函数，有：

定义2 均匀性适应度函数。

仅用fit，1度量个体的适应性是不够的，因为可能存在这样的个体，fit，1较大，但适应度向量中某个分量fi（X）较小，仍然不满足非劣性要求，因此，还需要定义个体的均匀性适应度函数：

式中：C为某个足够大的正常数。

2.4 遗传操作

以上设计的多目标适应度函数实际由2个适应度函数构成，因而，不能再采用标准遗传算法的选择算子。为此提出一种新型选择算子——多重选择算子。其执行流程是：首先以fit，1（X）为适应度对种群进行选择，得到一个中间种群；再以fit，2（X）为适应度对中间种群进行选择，得到新种群。其中2次种群选择的具体操作仍可采用赌轮选择，同时加入最优个体保护策略以保证全局收敛性。这样的选择过程逐代进行，可以使种群的非劣性逐步提高。交叉操作采用实数编码的部分离散杂交算子，变异操作采用实数编码的均匀变异算子。必须指出的是，对于实数编码，变异成为主要算子，变异概率较之二进制编码有较大增加。根据经验，二进制编码变异概率取值范围约为0.001～0.05，而实数编码的变异概率的取值范围约为0.2～0.5。

3 仿真实例

假设利用导弹攻击某一区域面积目标，目标的形状为长方形，长、宽分别为100m和400m。为了便于计算，假设目标的价值密度函数d（x，y）＝1，此时对目标毁伤的面积指标1与价值指标2相同，简化了计算。

现在考虑利用6枚同一类型导弹对该目标进行攻击，利用本文提出的方法求解最佳瞄准点。假设各导弹的杀伤半径为50m，标准差相同，均为10m，各枚导弹的射击相互独立，且弹着点随机散布。以攻击目标的一个角作为坐标原点，建立平面直角坐标系，如图3所示。

图3 目标区域示意图

假设第i个瞄准点的坐标为（xi，yi），则0≤xi＜200m，0≤yi＜50m，采用实数编码，精度为10－4m，即小数点后取4位，则染色体的长度为78。采用初始种群规模为100，交叉概率为0.75，变异概率为0.4，按照上面的进化规则对种群进行进化，进化100代，得到结果如下：最大毁伤面积为36 139.60m2，6枚导弹的瞄准点分别为（32.904 0，52.066 2），（118.395 6，55.683 9），（206.282 8，53.037 1），（275.600 9，87.675 8），（286.826 5，21.992 0），（356.534 4，49.954 5）（单位：m），如图4所示。

图4 导弹瞄准点分布图

从仿真实验结果可以看出，利用本文提出的算法得到的导弹瞄准点分布合理，用6枚导弹对此面积目标的面积毁伤即达到了90.35%，效果非常好。

4 结束语

本文通过分析面积目标的特点，首先建立了面积目标优化问题的指标函数，然后设计了一种面积目标射击效能遗传优化算法。该遗传算法采用实数编码，由于此问题为多目标优化问题，在选择算子中采用依托多个指标的选择算子，同时针对不同的射击情形，给出了各自的指标评价方程，在具体问题求解过程中具有很强的操作性。最后通过仿真实验，对本文提出的算法进行验证，得到了满意的结果。

［1］程云门.评定射击效率原理［M］.北京：国防工业出版社，2000.CHENG Yun－men.The theory of firing efficiency［M］.Beijing：National Defence Industry Press，2000.（in Chinese）

［2］王刚，段晓君，王正明.子母弹攻击复杂多区域面目标瞄准点选取方法［J］.弹道学报，2009，21（2）：27－30.WANG Gang，DUANG Xiao－jun，WANG Zheng－ming.Choosing method of aim points for cluster wavhead shooting complex multi－area target［J］.Journal of Ballistics，2009，21（2）：27－30.（in Chinese）

［3］李峰.地地战役战术导弹封锁敌港口时火力分配的优化［J］.战术导弹控制技术，2004（2）：60－62.LI Feng.Fire assignment optimization of ground－to－ground campaign tactical missile in blanking off enemy port［J］.Tactical Missile Technology，2004（2）：60－62.（in Chinese）

［4］雷宁利.混合相依目标群瞄准点优选方法研究［J］.系统工程与电子技术，2004，26（9）：1 234－1 235.LEI Ning－li.Optimizing method for aim points of mix－related targets［J］.Systems Engineering and Electronics，2004，26（9）：1 234－1 235.（in Chinese）

［5］GOLBERG D E.Genetic algorithms in search，optimization and machine learning［M］.London，England：Addison－Wesley Educational Publishers Inc，1989.

［6］FOGEL D B.A comparison of evolutionary programming and genetic algorithms on selected constrained optimization problems［J］.Simulation，1995，64（6）：397－406.

［7］HOMAIFER A.Constrained optimization via genetic algorithms［J］.Simulation，1994，62（4）：242－254.

［8］HAJELA P，LIN C Y.Genetic search strategies in multicriterion optimal design［J］.Structural Optimization，1992，5（4）：99－107.

［9］潘正君.演化计算［M］.北京：清华大学出版社，1998.PEN Zheng－jun.Evolutionary Computation［M］.Beijing：Tsinghua University Press，1998.（in Chinese）

［10］MICHALEWEICZ Z.Genetic algorithms＋data structures＝evolution programmings［M］.Berlin：Spring－verlag，1996.