底部排气圆柱体模型尾部流场的数值模拟
余文杰,余永刚,倪 彬
(1.南京理工大学 能源与动力工程学院,南京210094;2.北方信息控制集团有限公司,南京211153)
在超声速飞行时,弹箭底部存在低压回流区,会有很大的底部阻力[1]。向低压回流区内排气,可以增大底部压力,有效减小底部阻力[2]。
早期,Bowman[3]、Murthy[4]等人对冷排气、热排气、模型尾部形状、喷口大小和底部燃烧等方面进行过实验研究,大部分实验存在两方面的不足:①船尾、热排气、底部燃烧以及实验装置的缺陷等因素综合在一起,带来了较大的误差;②实验结果中缺少尾部流场的详细信息。Dutton等人[5-7]对某一马赫数下的同一种底部模型进行了一系列冷排气的实验研究,消除了这两方面的不足,使得数值模拟结果可以和实验进行详细的对比。
Sahu等人[8]最先运用较先进的数值计算方法研究冷排气情况。之后,Gibeling等人[9]建立了适用于数值模拟的底排燃烧化学反应模型,对底部热排气和底部燃烧现象进行了数值研究。Gibeling等人[10]又对M864底排弹的气动特性进行数值模拟,并和外弹道的数据进行了对比。近期热点回到冷排气上,侧重于通过和Dutton的实验进行对比来验证数值计算中湍流模型的准确性[11-12]。
图1为超声速来流圆柱体模型尾部流场示意图,图中,Ma∞为来流马赫数。来流经过尾部拐角时发生折转,产生膨胀波,并出现边界层分离,形成自由剪切层。在下游不远处,气体被压缩,产生再压缩激波,流动方向恢复成来流方向。在剪切层和圆柱底部之间形成一个封闭的回流区。尾部回流区内压力非常低,造成了很大的底部阻力。

图1 无底排的尾部流场示意图
向尾部回流区内排入少量气体可以大大改变尾部区域的流动特性。在冷排气下,对于给定的来流环境和尾部结构,改变的程度依赖于底部的排气质量流率[3]。图2为超声速来流底部排气的圆柱体模型尾部流场示意图,图中,Maj为喷口马赫数。由图可见,向尾部区域排入气体,原回流区尺寸变小,在喷口和拐角之间出现小的环状回流区。底排气体从2个回流区之间流入剪切层,改变了剪切层的形状,使分离流线变得平直,从而削弱外部的膨胀波和激波强度。外部的变化进一步影响到内部,使底部压力变大,底部阻力减小。

图2 有底排的尾部流场示意图
国内外关于底排尾部流场中环状回流区的变化以及底排气体出喷口后的流动规律的数值模拟未见文献报道。本文在和实验[5-7]进行对比验证的基础上,从尾部流场中的细节出发,数值研究底排增压减阻随排气参数变化的规律。
1 控制方程
假设尾部流场轴向对称,湍流模型选用SST模型。有限差分形式的二维轴对称Navier-Stokes方程为
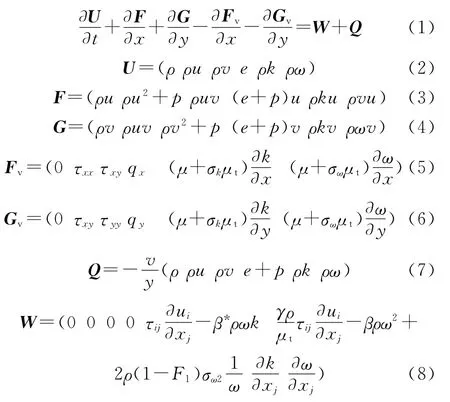
式中:ρ为密度,u为轴向速度,v为径向速度,ω为湍动能耗散率,k为湍动能,p为压力;U为守恒向量;F,G为对流矢通量;Fv,Gv为粘性矢通量;Q为轴对称源项;W为湍流源项;τ为粘性应力;e为单位体积总能;qx,qy为导热热流;μ为层流粘性系数;μt为湍流粘性系数;系数β*,σω2,σk,σω,β,γ,F1的给定方法参见 Menter的文献[13]。
2 模拟模型
数值模拟选用Dutton的实验模型[6-7],如图3所示。

图3 模型示意图
模型为圆柱体结构,x,y坐标方向分别表示轴向和径向;r0为底部半径;rj为喷口半径;Ma∞,p∞0,T∞0分别为来流马赫数、来流总压、来流总温;Maj,Tj0分别为喷口马赫数、喷口总温。I为排气参其中:Ab为底部面积为质量流率,ρ∞为来流密度,v∞为来流速度。实验具体参数值如表1所示。数,即质量流率的无量纲形式

表1 实验参数
3 模拟方法
采用有限体积法编程求解Navier-Stokes方程。对流项通过改进的AUSM+格式加入Van Leer限制器离散[14],粘性项采用局部坐标变换处理。时间离散采用 LU-SGS隐式时间推进方法[15],湍流和Navier-Stokes方程之间采用全耦合方法求解。粘性项采用近似隐式处理,湍动能生成项显式处理。
图4为模型尾部区域的网格图。图中远场采用无反射边界条件,固壁采用无滑移边界条件,中心轴线上采用对称边界条件,底排喷口的边界条件给定方法如下[12]。
先求出喷口马赫数Maj:
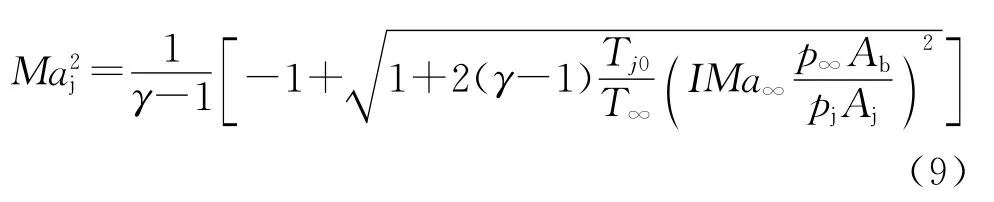
式中:Aj为喷口面积,来流静温T∞和来流静压p∞可由来流条件求出,喷口静压pj由流场中差值得到。得到Maj后,喷口的静温、密度、声速以及其他物理量就能相继求出。

图4 模型尾部区域网格图(网格数为35 000)
网格采用弧长法生成[16]。壁面第一层网格处y+控制在2以内,选取网格数分别为18 900,29 000,35 000的3套网格进行比较,以减小流场计算对网格的依赖性。排气参数取0.003 8,对图4中a、b两处的轴向速度进行研究。得到的速度分布如图5所示,其中v∞为来流速度,u为轴向速度。从图5(a)中可以看出,网格数量对径向靠近中轴线的流场有较大影响。从图5(b)中可以看出,网格数量对出喷口之后不久的中轴线上整个流场都有较大的影响。当网格数量大于29 000后,两图中轴向速度分布变化非常小,可以认为此时流场计算不受网格的影响。考虑到不同排气参数时网格影响可能不同,选用网格数为35 000的这套网格作为计算网格。

图5 不同网格数量对尾部流场的影响
4 数值计算结果及分析
对Ma∞=2.47,I=0~0.031 7排气参数范围内的模型尾部流场进行数值模拟,并对模型底部压力、尾部波系、尾部速度场以及底排减阻率进行研究。
4.1 底压分析
图6为模型底部面积平均压力p¯随排气参数变化曲线,p∞为来流静压,面积平均指的是底部固壁上的面积平均。压力随排气参数变化趋势和实验值[5-6]较吻合。随着排气参数的增加,底部面积平均压力先增大再减小,压力峰值出现的位置比实验值(I=0.014 8)略靠前。压力峰值对应的排气参数称为最佳排气参数。在小排气参数(I<0.005)时误差较小,在最佳排气参数附近(I=0.014 8)以及大排气参数(I>0.02)时误差较大,最大误差小于13%。
图7为小排气、最佳排气以及大排气3个状态下底部压力沿径向分布曲线。3个状态下数值模拟的模型底部压力沿径向的分布都很平直,和实验值[6]基本吻合。

图6 底部面积平均压力随排气参数变化曲线
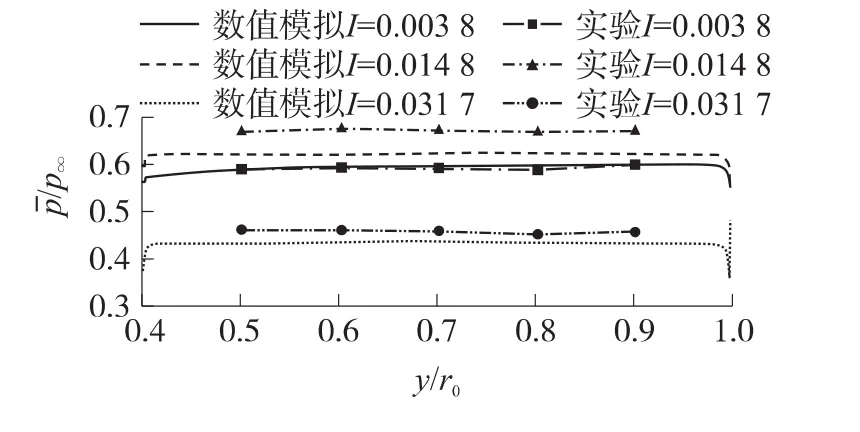
图7 底部压力沿径向分布曲线
4.2 尾部流场分析
图8 为无底排、最佳排气附近和大排气3种不同状态下模型尾部区域密度等值线。靠左边黑色区域为固壁,白色区域为喷口。
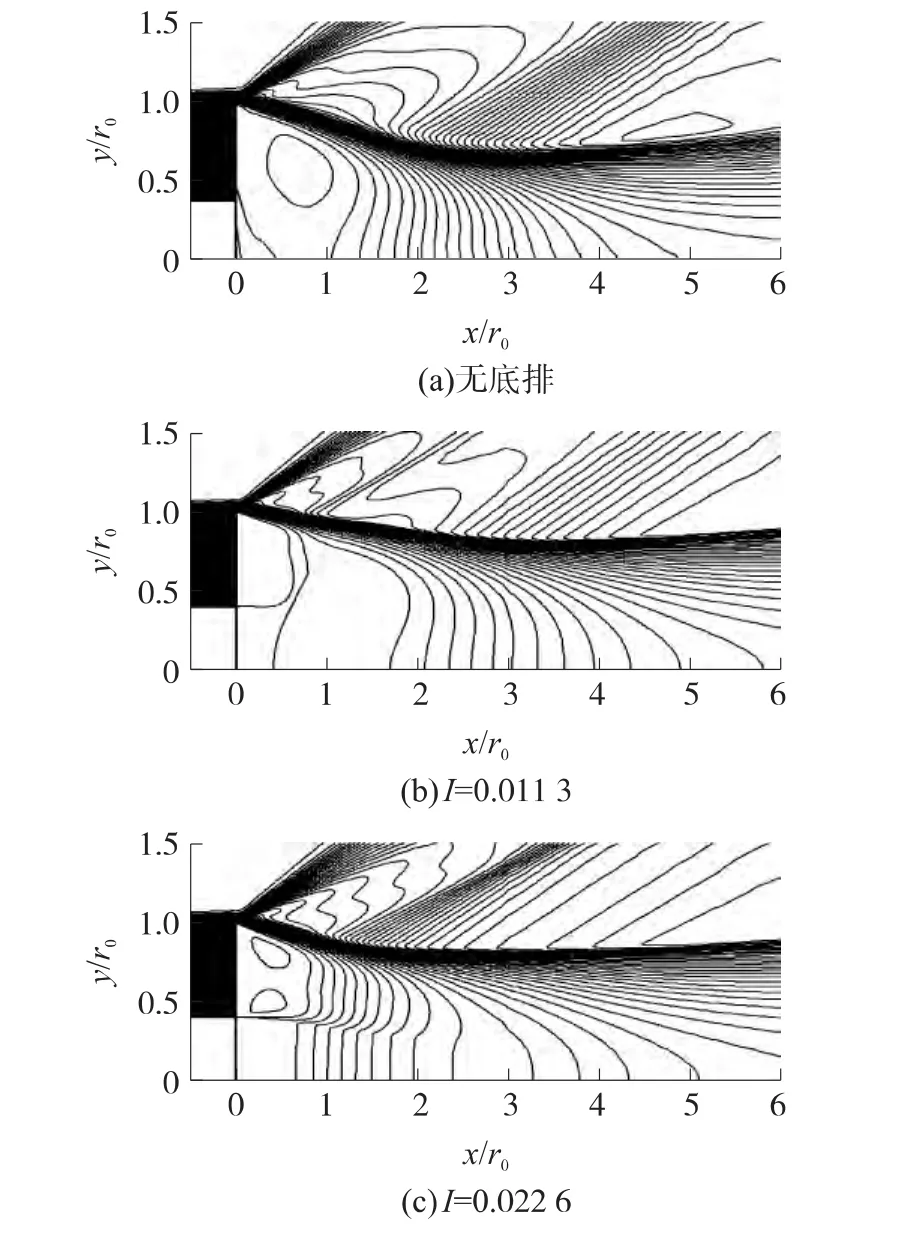
图8 尾部区域密度(ρ/ρ∞)等值线图
从图8中可以看出,无底排时尾部拐角处的膨胀角最大,下游喉部尺寸最小,再压缩激波最强(图8(a));在最佳排气参数附近,膨胀角变小,分离流线变得平直,再压缩激波强度减弱,有利于底排增压减阻(图8(b));在大排气参数下,膨胀角变大,分离流线又开始变陡,再压缩激波位置向上游移动,强度增大,不利于底排增压减阻(图8(c))。模型尾部的波系变化规律符合现实情况。
图9为小排气、最佳排气附近和大排气3种状态下尾部轴向速度等值线。
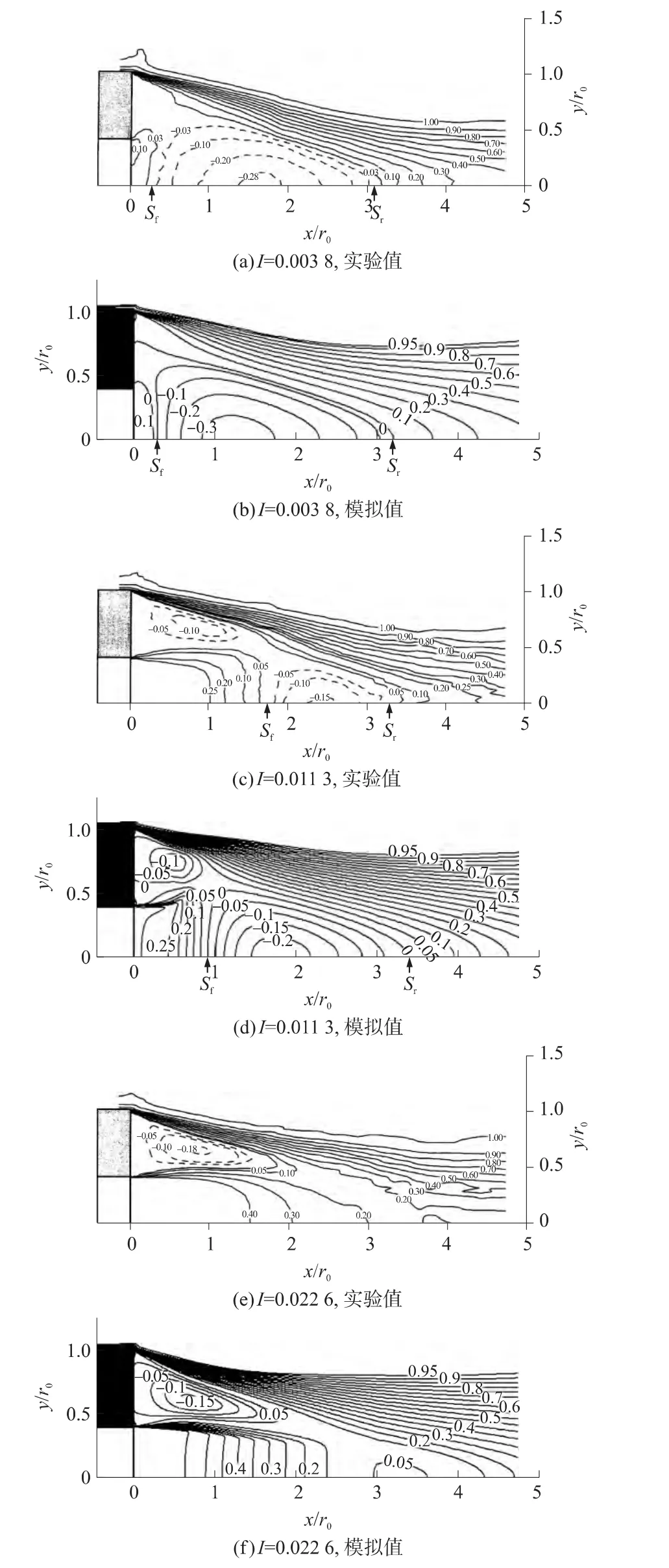
图9 尾部流场轴向速度等值线
图9(a)、9(c)、9(e)为实验值[7],图9(b)、9(d)、9(f)为模拟值,图中轴向速度用来流速度v∞无量纲化;Sf,Sr分别为前滞点和后滞点。
在小排气参数时(图9(a)、9(b)),模拟结果和实验值较吻合。回流区前、后滞点位置和实验基本相同,尾部流场中都未出现环状回流区。在最佳排气参数附近(图9(c)、9(d)),流场中出现环状回流区,主回流区的尺寸明显变小,模拟结果和实验值大体一样,只是模拟的主回流区比实验值更靠上游,更大一些,这可能是引起图6中底部压力在最佳排气参数附近和实验相差较大的原因。在大排气参数时(图9(e)、9(f)),模拟结果和实验较吻合,流场中环状回流区变大,主回流区消失,底排气体直接流入到远场。
可以看出:随着排气参数的增大,尾部流场中主回流区尺寸和强度逐渐减小,直到主回流区消失;而环状回流区由无到有,并且尺寸和强度不断增大。尾部中轴线上前滞点不断后移,后滞点位置变化很小,这是导致主回流区不断变小的直接原因。
图10为小排气、最佳排气附近和大排气3种状态下尾部流场速度云图,其中的曲线为流线。

图10 尾部流场速度云图
在小排气参数时(图10(a)),底排气体出喷口后立即折转,沿固壁流入底部拐角处的自由剪切层内,把固壁与回流区和剪切层隔离开来。同时,迅速流入自由剪切层的底排气体可以快速地改变剪切层形状,使剪切层和外流的边界——分离流线变得平直,从而削弱尾部的激波和膨胀波强度,进而快速有效地提高底部压力。如图6所示,在小排气参数时,底压增长率较大。
在最佳排气参数附近(图10(b))速度较大,底排气体出喷口后不会马上偏转流入外部的剪切层。这时,在底排射流形成的剪切层与外部自由剪切层之间的环状区域内形成小的回流区。环状回流区的出现使底排气体不能迅速有效地流入外部剪切层内,对底排减阻具有负面影响。随排气参数增加,环状回流区负面影响不断增大。在最佳排气参数时,负面影响和排气效果相抵消,底压达到峰值。这在图6中表现为,在小排气参数之后,底压增长率逐渐变小,过了最佳排气点,底压开始缓慢下降。
在大排气参数时(图10(c)),主回流区消失,底排气体直接流入到远场。如图6所示,在底排引射和环状回流区的共同作用下,底压迅速下降。
图11为底排减阻率随排气参数变化曲线,图中RCDB为底排减阻率,a、b、c三处分别对应图10中的小排气、最佳排气附近和大排气3种状态。从图中可以看出:小排气参数时底排减阻率迅速增加,排气参数大于0.005时,底排减阻率的增长开始变慢;最佳排气参数附近,底排减阻率随排气参数变化很小;大排气参数时,底排减阻率迅速下降。

图11 底排减阻率随排气参数变化曲线
5 结论
①数值模拟结果表明,模型底部面积平均压力随排气参数变化规律和实验较吻合,最大误差在最佳排气参数靠后段,其值小于13%。不同排气参数下模型尾部轴向速度场和实验大体一样,在最佳排气参数附近,原回流区尺寸比实验值更靠上游,且更大一些。
②在小排气参数时,底排气体贴着固壁流入剪切层,将固壁与回流区隔开。同时流入剪切层的底排气体使剪切层形状发生改变,从而削弱尾部的激波和膨胀波。因此,在小排气参数时,底压增加率较大。随着排气参数的增加,在底排剪切层和外部剪切层之间出现环状回流区,且其尺寸和强度也越来越大。环状回流区使底排气体不能快速有效地进入剪切层,对底部增压具有不利的影响。因此底压增长率开始逐渐变小,过了最佳排气点,底压开始缓慢下降。在大排气参数时,由于底排引射和环状回流区的共同作用,底压迅速下降。
[1]ROLLSTIN L.Measurement of inflight base pressure on an artillery-fired projectile[J].Journal of Spacecraft and Rockets,1990,27(1):5-6.
[2]郭锡福.底部排气弹外弹道学[M].北京:国防工业出版社,1995.GUO Xi-fu.Exterior ballistics of base bleed projectiles[M].Beijing:National Defence Industry Press,1995.(in Chinese)
[3]BOWMAN J E,CLAYDEN W A.Cylindrical afterbodies in supersonic flow with gas ejection[J].AIAA Journal,1967,5(6):1 524-1 525.
[4]MURTHY S N B,OSBORN J R.Aerodynamics of base combustion[M].Reston:AIAA,1976.
[5]HERRIN J L,DUTTON J C.Supersonic base flow experiments in the near wake of a cylindrical afterbody[J].AIAA Journal,1994,32(1):77-83.
[6]MATHUR T,DUTTON J C.Base bleed experiments with a cylindrical afterbody in supersonic flow[J].Journal of Space-craft and Rockets,1996,33(1):30-37.
[7]MATHUR T,DUTTON J C.Velocity and turbulence measurements in a supersonic base flow with mass bleed[J].AIAA Journal,1996,34(6):1 153-1 159.
[8]SAHU J,NIETUBICZ C J,STEGER J L.Navier-Stokes computations of projectile base flow with and without base injection[J].AIAA Journal,1985,23(9):1 348-1 355.
[9]GIBELING H J,BUGGELN R C.Projectile base bleed technology partⅠ:analysis and results,AD-A258 459[R].1992.
[10]DANBERG J E,NIETUBICZ C J.Predicted flight performance of base bleed projectiles[J].Journal of Spacecraft and Rockets,1992,29(3):366-372.
[11]PRAMOD S,GRAHAM V C.Numerical investigations of supersonic base flows using DES[C]//AIAA Aerospace Sciences Meeting and Exhibit.Reno,Nevada:AIAA,2005.
[12]SHIN J R,CHO D R,WON S H,et al.Hybrid RANS/LES study of base-bleed flows in supersonic mainstream [C]//AIAA International Space Planes and Hypersonic Systems and Technologies Conference.Dayton,Ohio:AIAA,2008.
[13]MENTER F R.Two-equation eddy-viscosity turbulence models for engineering application[J].AIAA Journal,1994,32(8):1 598-1 605.
[14]梁德旺,王可.AUSM+格式的改进[J].空气动力学学报,2004,22(4):404-409.LIANG De-wang,WANG Ke.Improvement of AUSM +scheme[J].Acta Aerodynamica Sinica,2004,22(4):404-409.(in Chinese)
[15]YOON S,JAMESON A.Lower-upper symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations[J].AIAA Journal,1988,26(9):1 025-1 026.
[16]武频,赵润祥,郭锡福.弧长网格生成法及其应用[J].南京理工大学学报,2002,26(5):482-485.WU Pin,ZHAO Run-xiang,GUO Xi-fu.Arc length method of grid generation and its application[J].Journal of Nanjing University of Science and Technology,2002,26(5):482-485.(in Chinese)

