导引头量测误差对落角约束最优制导律制导精度的影响

王 辉，林德福，王延东

（1.北京理工大学 宇航学院，北京100081；2.中国科学院 长春光学精密机械与物理研究所，长春130033）

随着现代战争形式的变化及精确制导技术的快速发展，在实现对敌方地面高价值目标精确攻击的同时，对末端攻击角度也提出了约束，如对装甲目标的掠顶攻击、对敌方舰船的掠海－俯冲攻击、航路点规划等。同时，很多战斗部的毁伤效能也与制导精度及末端攻击角度密切相关，从顶部以近似垂直的角度进行攻击可以达到更大的毁伤效果［1－2］。

传统上，人们基于线性化的制导模型已经提出了仅带落点约束、同时带落点和落角约束的最优制导律［2－4］。在弹目视线角为小角度假设下，可以将上述制导律简化成导弹加速度指令与弹目相对速度、弹目视线角、弹目视线角速度以及导弹剩余飞行时间的表达式，其中，弹目视线角速度为核心物理量，可以由平台或动力陀螺导引头直接测得［2－5］。简化后的制导律表达形式简单，易于工程实现。比例导引即为带落点约束的最优制导律的工程简化形式，在此基础上发展了若干衍生形式，如增强型比例导引、积分比例导引、近似积分比例导引等［6－9］。而习惯上，一般将带落点和落角约束的最优制导律简称为落角约束最优制导律。落角约束最优制导律是近几年的研究热点之一，相关的研究成果较多，如文献［1－5，10－13］等。

本文仅研究对地攻击的扩展落角约束最优制导律制导精度的一般性规律，根据文献［2－6，10－13］的描述，制导精度分别用脱靶量和落角误差表示。

1 扩展的落角约束最优制导律

传统的对固定目标最优的落角约束制导律表达式为［2］

式中：vr为弹目相对速度；ac为导弹加速度指令；q，分别为弹目视线角和角速度；qf为弹道终端期望落角；tgo＝tf－t，为剩余飞行时间，tf为制导时间。

根据文献［1］的研究成果，在利用最优控制理论推导制导律时，将控制权函数由1扩展为1／（n≥0），则引入参数n后的扩展落角约束最优制导律表达式为

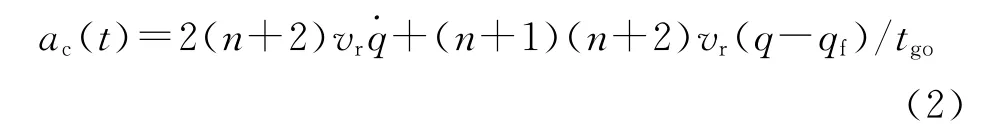
比较式（1）、式（2）可以看出，二者的导航系数之比由4∶2扩展为2（n＋2）∶（n＋1）（n＋2）。

为了表述方便，文中将扩展的落角约束最优制导律简写成EOGLIAC（extended optimal guidance law with impact angle constraint）。

2 导引头量测误差及制导动力学

2.1 制导动力学

对一个具有实际意义的制导系统，制导动力学是必须要考虑的内容，这其中包括导引头动力学、制导滤波器、驾驶仪动力学等。这些动力学既可能是高阶的，也可能是低阶的，这取决于建模的准确性及系统的需求。如对常规的两框平台导引头，用二阶或三阶环节来描述是合适的；对过载驾驶仪，工程上常用的是经典两回路、三回路驾驶仪或其变型，用二阶或三阶环节来描述也是合适的。上述导引头和驾驶仪模型都没有考虑惯性测量器件、滤波器、舵机等硬件动力学，一旦引入额外的硬件动力学，其阶数可能达到10阶、11阶。

在做制导系统精度分析时，若直接引入高阶的导引头和驾驶仪动力学模型，由于可变参数较多，很难得出通用性的结论。因此，为了便于理论研究、简化分析过程，通常将导引头和驾驶仪动力学简化成一阶或二阶环节来研究［2－8，10－13］。

2.2 导引头量测误差

导引头量测误差包括确定性误差和不确定性误差两类。对EOGLIAC制导系统，导引头不确定性量测误差主要是指视线角速率误差和视线角误差Δq以及初始方向误差（本文暂不考虑）；不确定性误差主要是指导引头量测噪声，本文仅考虑导引头探测器角噪声，相关模型可参考文献［2，5－6］，此处不再赘述。

3 导引头量测误差输入下的EOGLIAC制导系统

3.1 EOGLIAC制导系统模型的建立

根据式（2），引入导引头零位误差、探测器角噪声的EOGLIAC制导系统如图1所示。图中，Δq分别为导引头弹目视线角速率零位误差、弹目视线角零位误差；ua表示输入的探测器角噪声；K2a为对应的噪声功率谱密度，单位为rad2／（rad／s）；θ为弹道倾角；y′miss，θmiss分别为脱靶量和落角误差；s为拉普拉斯算子；Th，Ta和Tg分别表示导引头、驾驶仪和制导系统时间常数，其中，Tg＝Th＋Ta。

在对地攻击时，EOGLIAC又可表示成：

由式（3）可以看出，弹道倾角θ追踪弹目视线角q，在弹道末端θ（tf）与qf近似相等［12－13］，其中，tf为弹道的终端时刻。同时，导弹最终攻击目标时的有效角度是终端弹道倾角而非弹目视线角，弹道倾角比弹目视线角更具工程意义。因此，落角误差可根据θ（tf）－qf来计算［5，12］。

导引头和驾驶仪均为一阶环节，分别为1／（Ths＋1），1／（Tas＋1）。假设导引头和驾驶仪总滞后时间常数为Tg，改变导引头和驾驶仪动力学时间常数在总滞后时间常数中的权重，即可研究导引头和驾驶仪动力学的快速性比值对脱靶量的影响。表1给出了总滞后时间常数为Tg，Th／Ta分别为1／5，1／2，1，2，5时的动力学分配情况。

图1 3种误差输入下的落角约束最优制导律制导系统结构图

表1 导引头和驾驶仪动力学不同选取状态

3.2 无量纲的EOGLIAC 伴随系统

定义无量纲时间＝t／Tg，则＝s／Tg，＝tf／Tg－，其中，tf／Tg表示无量纲末导时间。经过无量纲和伴随模型变换，得到图2、图3所示的无量纲脱靶量和无量纲落角误差伴随模型。图中，k1＝分别表示弹目视线角及角速率零位误差、探测器角噪声引起的无量纲脱靶量；ymiss｜Δq，ymiss｜Δ，σmiss｜a为常规脱靶量；相应地｜Δq｜Δ，｜a为无量纲落角误差；θmiss｜Δq，θmiss｜Δ，σθmiss｜a为常规落角误差。图2、图3中的（）2表示对当前信号进行平方示对当前信号取平方根。

图2 脱靶量伴随系统结构图

由图2、图3的结果可以看出，弹目视线角零位误差引起的脱靶量与vr，Δq，Tg成正比，落角误差与Δq成正比；弹目视线角速率零位误差引起的脱靶量与vr，，T2g成正比，落角误差与，Tg成正比；探测器噪声引起的脱靶量与Ka，vr，成正比；落角误差与Ka成正比，与成反比。

图3 落角误差伴随系统结构图

由上面的分析可知，无量纲化前制导系统的可变参数有n，vr，Δq，，，Th，Ta，tf等8个，无量纲化后只有n，Th／Ta，tf／Tg等3个，因此，通过无量纲化有效地减少了可变参数，为后续脱靶量和落角误差的研究创造了方便。

4 EOGLIAC制导系统无量纲脱靶量和落角误差分析

根据制导系统的常规模型（图1）及无量纲伴随模型（图2、图3），对上述导引头量测误差作用下的位置和落角误差进行研究。在下面的仿真结果中，图的纵轴为各误差对应的无量纲脱靶量和落角误差，虚－实线表示伴随模型结果，离散圆点表示常规模型结果。

4.1 导引头视线角零位误差引起的无量纲脱靶量和落角误差分析

Δq作用下的无量纲脱靶量和落角误差如图4、图5所示。在图4（a）、图5（a）中，Th／Ta取为2；在图4（b）、图4（c）及图5（b）、图5（c）中，Th／Ta的取值规律如表1所示。

由仿真结果可以看出：对不同的指数n及不同的导引头和驾驶仪权状态，当tf／Tg≈15时，Δq引起的无量纲脱靶量收敛到零附近，无量纲落角误差收敛到－1附近；随着指数n的增大及导引头动力学时间常数的增加，无量纲脱靶量和落角误差振荡趋势加剧，峰值加大；与驾驶仪动力学相比，增加导引头的快速性能更有效地减少Δq对制导精度的影响。

下面对落角误差收敛到－1进行分析。由式（2）可知，落角约束项为（q－qf）／tgo，弹目视线角q追踪终端约束角qf；当弹目视线角有零位误差Δq时，落角约束项实际变为［q－（qf－Δq）］／tgo，弹目视线角q实际追踪的是qf－Δq。若末导时间足够长，在弹道末端，θf＝qf－Δq，则无量纲落角误差为（θfqf）／Δq＝－Δq／Δq＝－1，即上述仿真结果与理论分析是一致的。

4.2 导引头视线角速率零位误差引起的无量纲脱靶量和落角误差分析

图4 导引头视线角零位误差引起的无量纲脱靶量

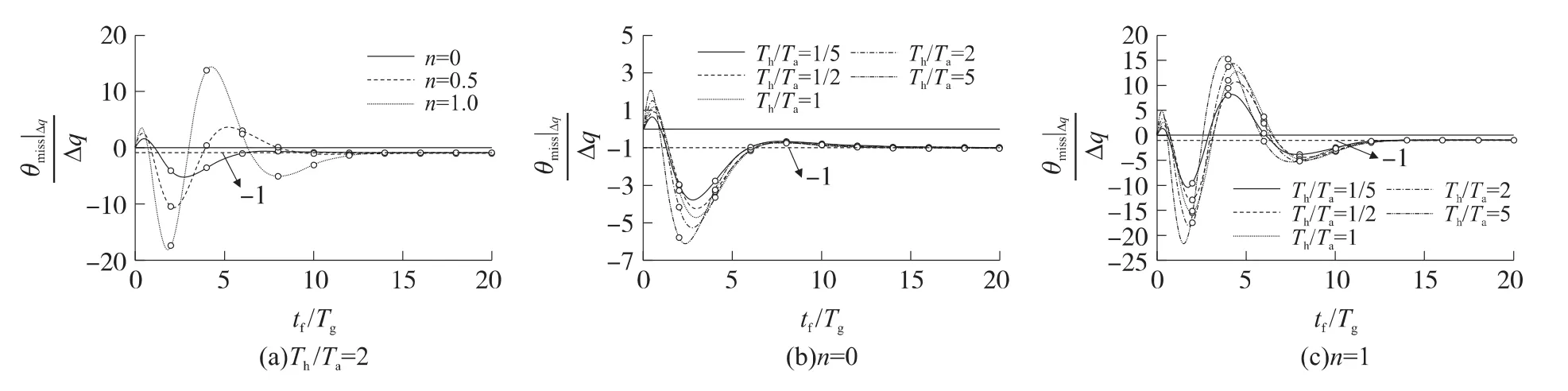
图5 导引头视线角零位误差引起的无量纲落角误差

图6 导引头视线角速率零位误差引起的无量纲脱靶量

图7 导引头视线角速率零位误差引起的无量纲落角误差

4.3 探测器噪声引起的无量纲脱靶量和落角误差分析

图8 、图9分别给出了探测器角噪声作用下的无量纲脱靶量和落角误差随tf／Tg和指数n（n∈［－0.5，1］）的变化曲线。由此可以看出：探测器角噪声引起的无量纲脱靶量和落角误差并不随tf／Tg的增大而趋向于零；当tf大于Tg的10倍时，脱靶量和落角误差达到稳态值，且随着指数n的增大，该稳态值显著增大。图8（b）、8（c），图9（b）、9（c）的仿真结果表明，在Tg一定及脱靶量和落角误差达到稳态值（tf／Tg＝15）的情况下，随着导引头和驾驶仪时间常数比值的变化，当导引头与驾驶仪响应速度一致时，系统无量纲脱靶量和落角误差均达到最大值。由于探测器噪声引起的脱靶量与T1／2g成正比，落角误差与T1／2g成反比，因此，在制导系统滞后时间常数一定的情况下，为了尽量降低探测器角噪声对制导精度的影响，指数n不应选得过大［2，6］。

图8 导引头探测器噪声引起的无量纲脱靶量

图9 导引头探测器噪声引起的无量纲落角误差

4.4 指数n的工程选取

根据式（2）中导航系数与参数n的关系式可知，指数n与导航系数一一对应，因此确定了指数n，也就确定了导航系数。指数n大时有利于消除导引头视线角速率零位误差引起的脱靶量，也能加快制导系统响应；但大的n会放大探测器角噪声引起的制导误差，也会使导引头视线角零位误差、落角约束、初始方向误差等引起的制导误差振荡加剧，收敛时间变长，同时在弹道初始段也容易造成过载饱和［6］。因此，制导系统工程师应根据导弹过载能力、各种误差引起的制导误差与总体技术指标间的关系，综合确定n的取值范围。

若以比例导引的导航系数N的最大取值6为上界，以传统的落角约束最优制导律的位置项导航系数4为下界，则可确定扩展的落角约束最优制导律的位置项导航系数的取值范围，进而可确定指数n的取值范围。根据2（n＋2）∈［4，6］，则指数n可取在0～1之间。

5 结论

本文以扩展的落角约束最优制导律为研究对象，针对地面固定目标，分别研究导引头视线角速率零位误差、视线角零位误差和探测器角噪声对制导精度的影响。研究结果表明：

①当末导时间达到制导系统滞后时间常数的15倍左右时，可以消除导引头视线角零位误差对脱靶量的影响。此时，导引头视线角零位误差引起的落角误差收敛到稳态值－1。

②大的指数n有利于消除导引头视线角速率零位误差对脱靶量和落角误差的影响。

③在导引头视线角速率和视线角零位误差作用下，提高导引头的响应比提高驾驶仪的响应更有利于降低制导误差。

④探测器角噪声引起的制导误差并不随着末导时间的增大而趋向于零，而是随着末导时间的增大收敛到稳态值，且指数n越大，稳态制导误差越大。因此，为了尽量降低探测器角噪声对制导精度的影响，指数n不应选得过大。

⑤参考比例导引及传统的落角约束最优制导律有效导航比的选择范围，建议指数n选在在0～1之间。

本文的研究方法同样适用于复杂的制导动力学模型，同时，文中的研究仅针对地面固定目标。若研究空中机动目标，需将目标机动补偿项引入到制导律中。

［1］OHLMEYER E J，PHILLIPS C A.Generalized vector explicit guidance［J］.Journal of Guidance，Control，and Dynamics，2006，29（2）：261－268.

［2］ZARCHAN P.Tactical and strategic missile guidance，5th edition［M］.Virginia：AIAA Inc，2007：31－50，541－569.

［3］常超，林德福，祁载康，等.带落点和落角约束的最优末制导律研究［J］.北京理工大学学报，2009，29（3）：233－239.CHANG Chao，LIN De－fu，QI Zai－kang，et al.Study on the optimal terminal guidance law with interception and impact angle［J］.Journal of Beijing Institute of Technology，2009，29（3）：233－239.（in Chinese）

［4］WANG H，LIN D F，CHENG Z X.Time－to－go weighted optimal trajectory shaping guidance law［J］.Journal of Beijing Institute of Technology，2011，20（3）：317－323.

［5］刘大卫，夏群利，崔莹莹，等.具有终端位置和角度约束的广义落角约束最优制导律［J］.北京理工大学学报，2011，31（12）：1 408－1 413.LIU Da－wei，XIA Qun－li，CUI Ying－ying，et al.Generalized trajectory shaping guidance law with both impact position and angle constrains［J］.Journal of Beijing Institute of Technology，2011，31（12）：1 408－1 413.（in Chinese）

［6］GARNELL P.Guided weapon control systems［M］.Beijing：Beijing Institute of Technology Press，2003：297－364.

［7］王辉，林德福，祁载康，等.时变最优的增强型比例导引及其脱靶量解析研究［J］.红外与激光工程，2013，42（3）：692－698.WANG Hui，LIN De－fu，QI Zai－kang，et al.Study of time－varying optimal augmented proportional navigation and miss distance closed－form solutions［J］.Infrared and Laser Engineering，2013，42（3）：692－698.（in Chinese）

［8］张宏，夏群力，祁载康，等.基于目标机动补偿的增强型比例导引性能研究［J］.红外与激光工程，2007，36（1）：82－87.ZHANG Hong，XIA Qu－li，QI Zai－kang，et al.Augmented proportional navigation with maneuvering target compensation［J］.Infrared and Laser Engineering，2007，36（1）：82－87.（in Chinese）

［9］PRASANNA H M，GHOSE D.Retro proportional navigation：a new guidance law for interception of high speed targets［J］.Journal of Guidance，Control，and Dynamics，2012，35（2）：377－386.

［10］BEN－ASHER J Z，YAESH I.Optimal guidance with reduced sensitivity to time－to－go estimation errors［J］.Journal of Guidance，Control，and Dynamics，1997，20（1）：158－163.

［11］BEN－ASHER J Z，YAESH I.Advances in missile guidance theory［M］.Virginia：AIAA Inc.，1998：25－88.

［12］RYOO C K，CHO H，TAHK M J.Optimal guidance laws with terminal impact angle constraint［J］.Journal of Guidance，Control，and Dynamics，2005，28（4）：724－732.

［13］RYOO C K，CHO H，TAHK M J.Closed－form solutions of optimal guidance with terminal impact angle constraint［C］／／Proceeding of IEEE International Conference on Control Application.Istanbul，Turkey：IEEE，2003：504－509.