基于末段修正迫弹命中概率的射角优化

李兴隆，于纪言，姚文进，王晓鸣，吴 巍

（1.南京理工大学 智能弹药技术国防重点学科实验室，南京210094；2.中国人民解放军63863部队，吉林 白城137001）

激光半主动末段修正迫弹的工作原理是利用弹外目标指示器发射激光束照射目标，然后弹载激光探测器通过接收的目标反射激光信号得到目标方位信息，弹载处理器生成修正指令控制执行机构（如舵机或脉冲发动机）工作，实现对末段弹道的修正［1］。

常规迫弹发射时以无控弹道落点为目标点，在理想情况下，迫弹能够捕获并命中目标，但在实际发射和飞行过程中受到多种随机干扰，导致弹道偏离名义弹道，末修迫弹导引头有可能一直无法捕获目标，造成脱靶，尤其是在小射角范围45°～57°内，影响效果明显；在大射角范围57°～85°内，由于落角较大，导引头在地面的视场一般都会覆盖目标，不易脱靶。导引头的视场角、作用距离、弹体姿态角和弹体位置坐标都与捕获概率有关［2］，修正执行机构的启控时间、最大修正能力、末制导律和控制策略［3－5］等都与命中概率有关，而以上因素均受到弹丸发射角的影响。因此，本文主要从优化发射角的角度研究了提高末修迫弹对目标命中概率的方法。

1 末段修正弹命中过程建模

1.1 末段修正弹命中目标的物理过程

弹丸出炮口后进行无控飞行，在弹道末段，当目标进入导引头最大作用距离Lmax内，且目标在导引头视场内，即跟踪误差角ε小于导引头探测器视场角φ时，可认定导引头捕获目标，其表达式为［6］

文中取Lmax＝3km，φ＝±6°。末段修正弹导引头捕获域示意图如图1所示。

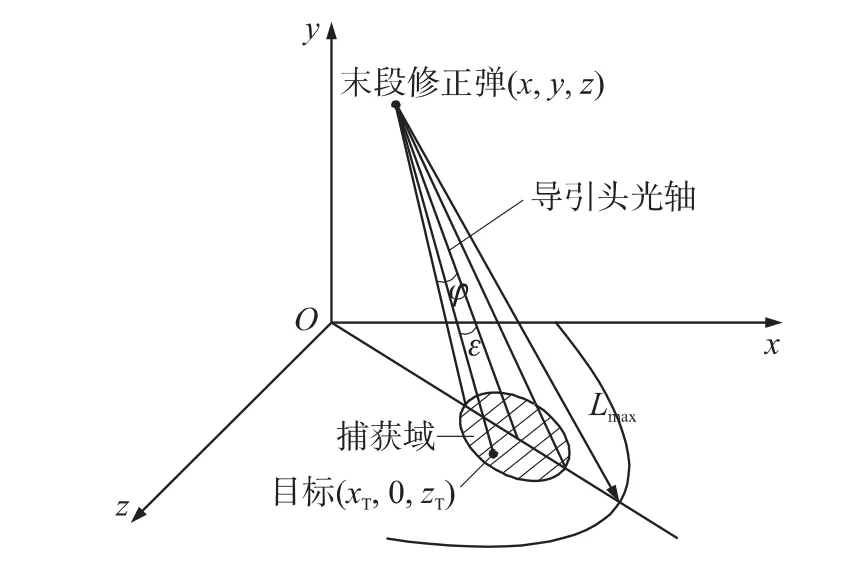
图1 捕获域示意图

导引头捕获到目标后由弹上计算机决定启控时机，进入有控飞行阶段，由执行机构修正末段弹道。若目标在最大修正区域内，则有可能命中目标。令事件A为捕获目标，事件B为命中目标，两事件相互独立，末修迫弹总命中概率的数学模型可表述为

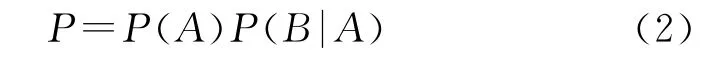
式中：P（A）为捕获概率，P（B｜A）为已捕获目标的条件下命中目标的概率。

1.2 捕获概率模型

末修迫弹导引头的捕获概率和命中概率都与启控距离有关，启控距离越大，修正能力越强。若启控距离过大，则末段修正弹道越长，受到的不确定因素的影响就越大，修正精度就越低；若启控距离过小，则修正执行机构来不及响应，或者由于启控过晚导致最大修正量小于落点偏差量，都会导致脱靶。为研究导引头捕获概率的一般规律，经估算后，取启控距离δ＝1km，此时修正能力基本满足要求，且δ＜Lmax。若此刻跟踪误差角ε≤｜φ｜，则捕获到目标，反之则未捕获。

由于弹丸发射和飞行过程中受到各种随机扰动，在启控距离δ＝1km时刻，误差角ε服从正态分布，ε～N（με，σ2ε）。将初始扰动模型和飞行过程中随机扰动模型［7］引入到弹丸六自由度弹道模型［8］中，利用蒙特卡洛方法模拟打靶n次，可得出跟踪误差角均值με和标准差σε。

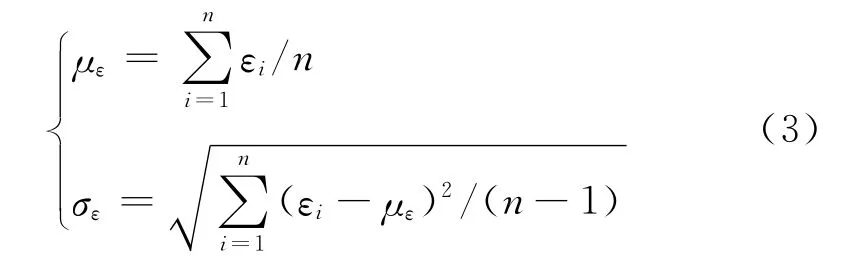
跟踪误差角ε≤｜φ｜的概率即为导引头对目标的捕获概率，可由下式求取：

可转化为下式查标准正态分布表进行求解：

由式（5）可知，捕获概率是关于误差角ε的函数。由激光探测器模型［9］可知，误差角是由质心位置（x，y，z）和姿态角（ϑ，ψ）决定的（ϑ为俯仰角，ψ为偏航角），在6DOF弹道方程中，若时间确定，则（x，y，z）和（ϑ，ψ）只与初始条件有关，若初速一定，不考虑初始扰动误差，则在δ＝1km时刻弹丸捕获目标的概率P（A）＝f（θ）是关于发射角θ的函数。

1.3 捕获条件下命中概率模型

弹丸在发射和飞行过程中受到的扰动越大，则弹道偏离名义弹道越大，即使在导引头探测器作用距离内捕获到目标，也可能由于修正能力不够导致脱靶。为研究已捕获目标条件下弹丸能否命中目标问题，取弹丸在启控距离δ＝1km处的最大修正量为lx＋，lx－ ，lz＋，lz－ 。lx＋，lx－ ，lz＋，lz－ ，分别 表 示 射程x向正向、射程x向负向、偏流z向正向、偏流z向负向4个方向上的最大修正距离。

令目标的有效毁伤幅员是以目标点为中心的矩形，矩形的边分别平行于x轴、z轴，正面为2Lz，纵深为2Lx。只要弹丸落在该幅员内，目标必然被毁伤。

由射击理论的假设可知，无控弹道的落点x，z服从二维正态分布定律，且相互独立，概率论中这种分布概率密度f（x，z）的数学描述式为

类似于1.2节，通过蒙特卡洛法模拟打靶，若在启控距离δ＝1km时导引头捕获目标，则转入命中概率的计算，得到已捕获目标情况下落点坐标均值（μx，μz）和 标 准 差 （σx，σx）。 记 目 标 点 坐 标 为（xT，zT），若 无 控 弹 道 落 点 （xi，zi）满 足，则在距离δ＝1km时启控，弹丸能命中目标。

因此，命中概率就等于概率密度函数f（x，z）在此区间的积分：

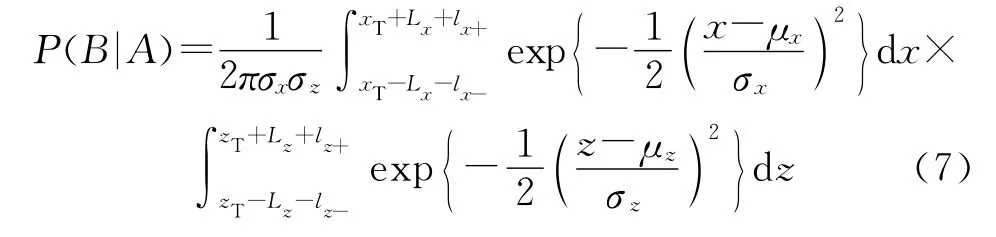
可转化为下式查标准正态分布表进行求解：

由于弹丸落点与发射角θ有关，因此，命中概率P（B｜A）＝g（θ）是关于θ的函数。

1.4 命中概率计算流程

根据上述命中目标的物理过程和数学模型，结合蒙特卡洛法仿真数据，即可求解命中概率，计算流程图如图2所示。

图2 命中概率计算流程图

1.5 平均落点偏差计算模型

令目标点坐标为（xT，zT），取发射角为θ，用蒙特卡洛法模拟打靶n次，得到弹丸无控飞行的n个落点，平均落点偏差用R表示，其计算公式如下：

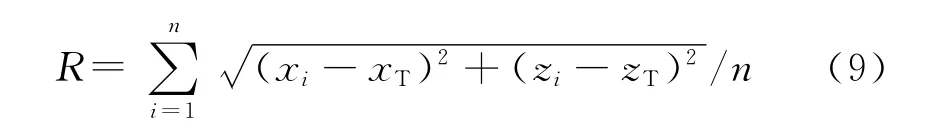
显然，平均落点偏差R是关于发射角θ的函数，即R＝h（θ）。落点偏差越大，则表明实际弹道偏离名义弹道越多，弹丸命中目标所需的修正量也越大；落点偏差越小，则所需修正量越小，则越容易修正。修正量的大小与命中率直接相关，因此，平均落点偏差也是研究命中概率不可忽略的因素。

2 优化数学模型的建立

2.1 设计变量及目标函数的确定

单发命中率是评价末修迫弹性能优劣的指标之一，同时，弹丸无控飞行的平均落点偏差越小，则越容易修正。因此，以末修迫弹最大命中率maxP（X）和最小落点偏差minR（X）为目标函数。由前文得P＝P（A）P（B／A）＝f（θ）g（θ），R＝h（θ），末修迫弹总命中率P和平均落点偏差R均是关于发射角θ的函数，因此，以发射角为优化设计变量，即X＝θ，此问题转化为单变量双目标函数的优化问题。

2.2 约束条件

常规迫弹命中误差在70～80m以上，要命中目标常常需要较大的火力密集度才能完成，而末修迫弹杀伤力要求是2发或更少就能命中目标［10］，令2发末修迫弹命中目标的概率大于90%即可认为达到精度要求，根据1－（1－P（X））2≥90%，可得到单发末修迫弹命中概率约束条件为P（X）≥68.38%。令给定射程的名义发射角为θ＊，变量的取值约束条件为θ＊－4≤X≤θ＊＋4。

2.3 优化算法

多目标规划解法的基本思想是转化为单目标规划问题，功效系数法就是其中的一种方法。其主要内容是对不同类型的目标函数统一量纲，分别得到一个功效系数函数，然后求所有功效系数乘积的最优解。

命中概率单项功效系数为

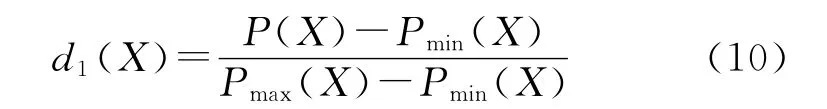
平均落点偏差单项功效系数为

总功效系数为

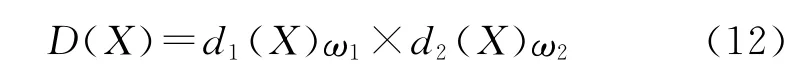
式中：ω1，ω2分别为单个评价指标的权重系数，当总功效系数D取最大值时，对应的X即为问题的最优解。

3 算例分析

根据以上优化模型可对给定射程的发射角进行优化设计。以某型末修迫弹为研究对象，导引头视场角φ＝±6°，目标点坐标为xT＝7 189m，zT＝－19m，名义发射角θ＊＝49°，启控距离δ＝1km，对应启控距离下4个方向上的最大修正量［11］为lx＋＝169m，lx－ ＝143m，lz＋＝133m，lz－ ＝133m，武器系统综合可靠性为95%，蒙特卡洛法计算机模拟打靶次数n＝200，单个评价指标的权重系数ω1＝0.5，ω2＝0.5。

3.1 计算结果

通过第2章的数学模型计算得出命中概率和平均落点偏差，结果如表1所示。

表1 命中概率和平均落点偏差计算结果

由表1得知，以名义射角49°发射的迫弹平均落点偏差最小，但其命中概率不及射角50°和射角51°的高，原因在于以名义射角发射的炮弹落点散布在目标点周围，部分弹道偏差过于靠前，这导致弹丸在整个末段弹道飞行过程中目标都不会进入导引头视场域中或进入视场域的时机过晚，弹道偏差无法得到及时修正，以至于脱靶。而增加射角后弹丸落点偏后，目标进入视场内的时机更早，捕获目标的概率更大［12］，但若落点偏差过大，超过最大修正能力，也会导致脱靶，因此存在一个最优射角，使捕获和命中的概率最大。

3.2 多项式拟合

为研究最优射角，需要得到目标函数，利用多项式拟合得到的函数能较准确地描述变量与函数值的关系。以发射角为自变量，对表1中的命中概率和平均落点偏差进行多项式拟合，得到的多项式分别为

图3、图4中虚线表示计算结果数据，曲线为拟合值，结果显示多项式拟合与计算值能较好地符合。

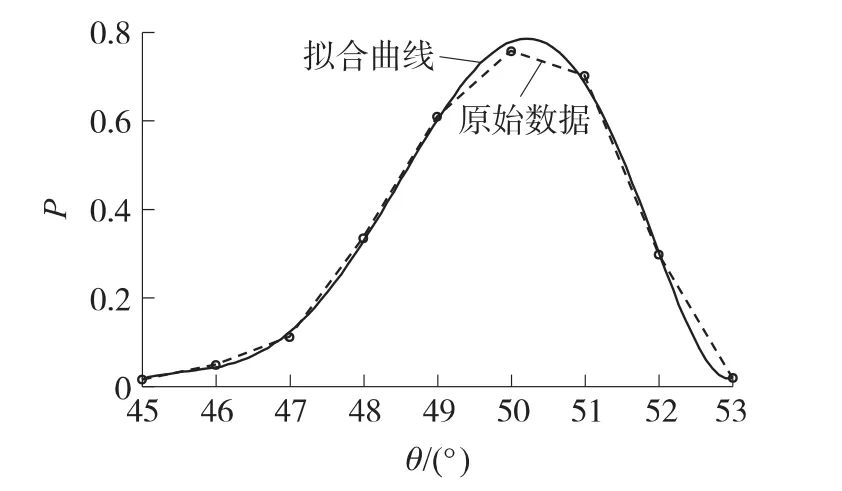
图3 不同发射角命中概率

图4 不同发射角平均落点偏差

3.3 优化结果

将3.2节得到的2个目标函数代入到功效系数表达式中，可得到总功效系数关于射角的函数。图5给出了不同发射角下总功效系数曲线。通过一维搜索黄金分割法可求出最大总功效系数max［D（X）］＝0.917，对应的射角X＝49.87°，即为最优射角，射角优化后命中概率为P（X）＝0.767。

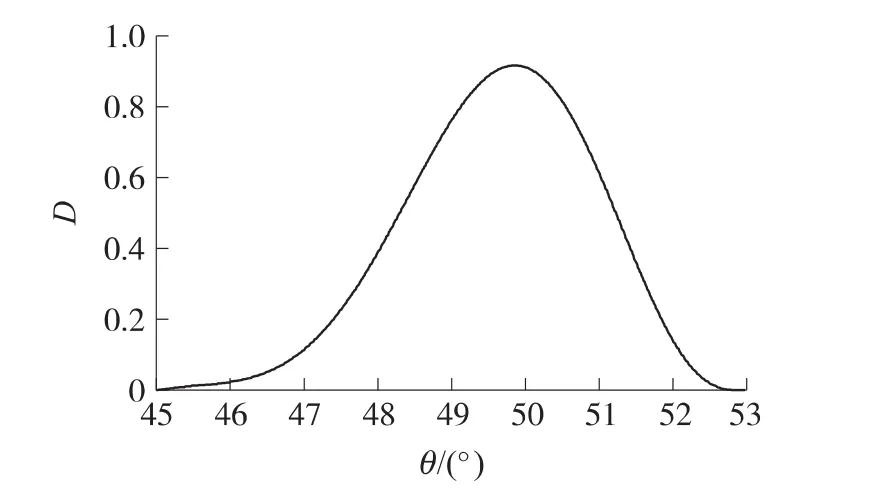
图5 不同发射角总功效系数

3.4 结果对比

分别以射程方向x＝6 616，6 967，7 198，7 310m处为目标点，通过以上方法对其射角进行优化，优化前后的命中率如表2所示。结果表明，射角优化的方法对提高命中率效果显著。

表2 不同目标距离射角优化前后命中率对比

4 结束语

本文考虑了末修迫弹发射时初始随机误差和飞行过程中随机扰动的情况，推导了命中目标概率的计算模型，以发射角为优化变量，提出了以最大命中率和最小平均落点偏差为目标函数的优化算法。仿真和计算结果表明，当目标在6 600～7 300m远处，通过射角优化，命中概率可提高10%以上，当目标距离小于6 600m时，命中概率已经很高，优化意义不大。该方法有效地弥补了利用常规射表发射末修迫弹时，激光导引头对目标捕获率低导致脱靶的问题，对于提高激光半动末修迫弹的命中精度具有重要意义。同时该方法对编制激光半主动末修弹药的射表具有一定的参考价值。

［1］郭泽荣.基于激光半主动的弹道修正系统修正能力的研究［J］.光学技术，2008，34：321－325.GUO Ze－rong.Study on the correction system based on semiactive laser［J］.Optical Technique，2008，34：321－325.（in Chinese）

［2］李国英.末制导炮弹攻击区仿真研究［J］.弹道学报，1997，9（1）：69－72.LI Guo－yin.Simulation of terminal guidance projectile attack area［J］.Journal of Ballistics，1997，9（1）：69－72.（in Chinese）

［3］刘巍，芮筱亭，王国平.简易修正弹末段弹道修正能力分析与优化设计［J］.南京理工大学学报，2006，30（4）：449－453.LIU Wei，RUI Xiao－ting，WANG Guo－ping.Terminal trajectory correction capability analysis and optimization design for control projectile［J］.Journal of Nanjing University of Science and Technology，2006，30（4）：449－453.（in Chinese）

［4］徐劲祥.弹道修正弹追踪制导律研究［J］.弹箭与制导学报，2004，24（4）：163－165.XU Jin－xiang.A study on pursuit guidance law of trajectory correction projectiles［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2004，24（4）：163－165.（in Chinese）

［5］姚文进，王晓鸣，李文彬，等.末段修正迫弹脉冲发动机控制策略［J］.探测与控制学报，2008，30：8－14.YAO Wen－jin，WANG Xiao－ming，LI Wen－bin，et al.Control strategy of pulse engine in terminal correction mortar［J］.Journal of Detection ＆ Control，2008，30：8－14.（in Chinese）

［6］林德福，牟宇，常超，等.激光半主动末制导炮弹捕获概率研究［J］.北京理工大学学报，2010，30（6）：698－701.LIN De－fu，MOU Yu，CHANG Chao，et al.A study of target acquisition probability for laser semi－active terminal guided projectile［J］.Transaction of Beijing Institute of Technology，2010，30（6）：698－701.（in Chinese）

［7］曹小兵.脉冲末修迫弹弹道特性分析与控制方案设计［D］.南京：南京理工大学，2012.CAO Xiao－bing.Analysis of ballistic characteristics and design of control scheme for terminal trajectory correction mortar projectile equipped with lateral impulses［D］.Nanjing：Nanjing U－niversity of Science ＆ Technology，2012.（in Chinese）

［8］韩子鹏.弹箭外弹道学［M］.北京：北京理工大学出版社，2008.HAN Zi－peng.Exterior ballistics of projectile and rocket［M］.Beijing：Beijing Institute of Technology Press，2008.（in Chinese）

［9］徐劲祥.末段修正迫弹激光探测器及目标方位模型［J］.兵工学报，2007，27（7）：793－795.XU Jin－xiang.Models of laser detector and target azimuth for terminal correction mortar projectile［J］.Acta Armamentarii，2007，27（7）：793－795.（in Chinese）

［10］一平.中国120毫米末修迫击炮弹武器系统［J］.兵器知识，2007，10：24－25.YI Ping.Chinese 120mm terminal correction mortar projectile weapon system［J］.Ordnance Knowledge，2007，10：24－25.（in Chinese）

［11］王浩磊.基于脉冲控制的迫弹弹道末段修正研究［D］.南京：南京理工大学，2012.WANG Hao－lei.Study on terminal correction trajectory based on impulse control［D］.Nanjing：Nanjing University of Science＆ Technology，2012.（in Chinese）

［12］LI Xing－long，WANG Xiao－ming，YAO Wen－jin，et al.Optimization of launching angle based on the acquisition probability for laser semi－active terminal correction projectile［C］／／2nd International Conference on Opto－Electronics Engineering and Materials Research.Zhengzhou：Trans Tech Publication Ltd，2013：209－212.