基于Gauss伪谱法的滑翔弹道快速优化

陈 琦，王中原，常思江

（南京理工大学 能源与动力工程学院，南京210094）

随着战争理念的进步和发展，特别是现代非对称作战中“远程压制、精确打击、高效毁伤”等概念的提出，传统火炮射程不远、精度不高等缺点逐渐暴露，已不能适应现代战争的需求。在这种背景下，滑翔增程制导炮弹以其反应速度快、效费比高、使用灵活并且可打击静止和运动目标等优势逐渐受到各国的重视。滑翔増程弹由火炮发射后，尾翼张开保持稳定飞行，之后火箭发动机启动并开始助推，发动机工作结束后，弹丸像普通尾翼弹一样继续在升弧段上飞行，到达弹道顶点附近，鸭舵展开，开始对弹丸实施控制，最终命中目标。文献［1－4］阐述了滑翔増程弹的飞行原理；文献［5］研究了制导炮弹最优滑翔弹道与控制问题，分别采用庞特里亚金极大值原理和共轭梯度法求解了控制变量有约束的最优滑翔弹道；文献［6］对滑翔弹道分3段进行了分析，研究了滑翔増程炮弹的弹道模型，并对滑翔弹道进行了设计。文献［7］以最大升阻比的方法对滑翔弹道进行了优化设计；文献［8］分别采用了序列二次规划法和最大升阻比法优化了俯仰舵偏角规律。以上文献主要以射程最远为性能指标优化方案弹道，这对于考察弹丸的滑翔能力、打击距离均具有十分重要的意义。但是这种方法也往往使得优化出的弹道飞行时间过长，易被敌方防御系统发现和拦截；存速较低，削弱了末端攻击的机动性。这在很大程度上限制了制导炮弹快速精确打击、及时火力支援等能力的发挥。此外，上述研究均假设攻角能瞬时响应指令信号，导致设计出的方案弹道过于理想，给实际应用带来了较大的难度。针对以上问题，本文以飞行时间为性能指标对滑翔弹道进行了优化设计，考虑了动力学滞后，将其简化为一阶惯性环节，引入了虚拟控制量，并将其作为优化变量，同时为了保证攻击效果，对末端存速、落角进行一定的限制，在纵向平面内建立了弹道优化模型；引入了伪谱理论对模型进行离散，这在很大程度上降低了弹道优化耗时，缩短了滑翔弹的作战反应时间，同时也为今后实现算法的实时性提供了理论依据。

1 弹道优化问题描述

1.1 滑翔増程弹运动方程

为研究问题的本质，本文只考虑炮弹在纵向平面内的运动，并将动力学滞后简化为一阶惯性环节，大气为标准气象条件。在这种情况下，滑翔増程制导炮弹的滑翔段运动方程可简化为

Fx，Fy分别为阻力和升力，有：

式中：θ为弹道倾角，q为动压，Sref为参考面积，k和k′分别为弹翼组合体和舵面的诱导阻力系数，Cx0BW和Cx0δ分别为弹翼组合体和舵面的零升阻力系数，和Cδz

y分别为弹翼组合体和舵面的升力系数导数，以上各参数的值由吹风实验获得。αB和δzB分别为平衡攻角和平衡舵偏角，Td为一阶惯性环节的时间常数，uα为虚拟控制量，ε（uα）＝0为虚拟量uα的控制方程。方程中其它变量的意义参见文献［9］。

1.2 弹道优化模型

为了实现快速打击的要求，滑翔増程制导炮弹在弹道最高点处张开鸭舵，对弹体实施控制，经过滑翔飞行，在最短的时间内命中目标，同时，为了保证对目标的毁伤效果，还要对弹道末端速度和落角进行一定的限制。因此，滑翔弹道优化问题可以具体描述为：在［0，tf］时间内（tf为未知的弹道末端时刻），确定出控制量uα，使得由式（1）确定的动态系统从初始状态转移到终端状态，在满足规定约束的条件下，使得参数tf最小。由以上分析可知，弹道优化问题实际上是一个动态优化问题，其优化模型可表示如下：

①性能指标。为了实现快速打击的要求，性能指标取为攻击时间最短，即：

②初始状态为无控段末端状态，本文取为弹道最高点处状态。

③终端约束条件。为了保证最终的攻击效果，滑翔段终端状态应满足一定的约束，包括终端位置约束、速度约束和落角约束，即：

④攻角约束。考虑到弹体的控制性能，同时避免弹体失速，需要对攻角的幅值进行约束，即：

⑤系统状态方程为式（1）描述的弹体纵向平面运动模型。

可见，滑翔弹道优化问题是一个起始状态固定，终端状态受约束，终端时刻自由的非线性动态优化问题。

2 Gauss伪谱法

作为一种求解最优控制问题的直接方法，Gauss伪谱法的主要思想是将连续的无限维最优控制问题转换为非线性规划问题进行求解，在一系列的Legendre－Gauss（LG）节点上将状态变量和控制变量进行离散，并且利用这些离散点构造全局Lagrange插值多项式来近似系统的动力学方程。该方法具有收敛速度快、对初值不敏感且无需猜测协态变量等优点，2005年经Benson D在其博士论文中介绍并完善后［10］，便受到了广泛的关注和应用。

2.1 系统动力学方程离散

考虑积分形式的系统动力学方程：

式中：X（t）∈Rn为状态向量，U（t）∈Rm为控制向量，f：Rn×Rm×R→Rn为连续向量函数。采用Gauss伪谱法需要将时间区域［t0，tf］转换到［－1，1］上，为此，引入变量τ对时间t进行变换［6］，即：

因此，系统动力学方程变为

由数值分析的知识可知，选取N个Lagrange插值基函数Lk（ζ）近似式（4）中的积分项，其代数精度可达2N－1次［11］，有：

这样，结合式（4）和式（5），第i个节点处的状态向量便可表示为

若记X0＝X（－1），Ui＝U（τi），Xi＝X（τi），1≤i≤N，根据式（6），便可将积分形式的系统动力学方程在N个LG节点上转换为代数方程，即：

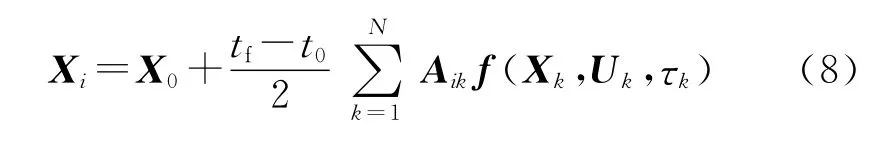
式中：Wi为第i个节点处的积分权重，Wi＝

2.2 边界条件和性能指标离散

式（8）仅在区间的内点计算状态量，并未包含终端时刻节点，终端状态应满足动力学方程约束，即：

将终端条件离散并利用Gauss积分来近似，可得：

由于本文所选取的性能指标为Mayer型指标，不包含积分项。因此无需进行特殊处理，即：

根据以上的数学变换，本文的问题可以描述为：在［t0，tf］时间内（tf为未知的弹道末端时刻），确定离散点上的状态向量Xi（i＝1，2，…，N）、控制向量Ui（i＝1，2，…，N）和终端时刻tf，使得性能指标（11）最小，并满足系统动力学方程约束（8）、终端状态约束（10），以及原问题的边界条件和过程约束：

从而将连续的无限维最优控制问题转换为一般的非线性规划问题，写成标准形式为

3 数值仿真算例

以某滑翔增程制导炮弹为对象进行数值仿真。经火箭发动机助推后弹丸质量m＝37.27kg，炮弹达到弹道最高点时的高度为Hp0＝14 746.6m，速度为vp0＝299.3m／s，弹道倾角为θp0＝0；滑翔段舵偏角约束为｜αB（t）｜≤15°，滑翔末端高度取为yf＝0，弹道倾角取为｜θ（tf）｜≥θf＝89°，同时，为了保证攻击效果，也要对末端存速进行限制，v（tf）≥vf＝200m／s，一阶惯性环节的时间常数Td取为1.5s。取弹道最高点处x0＝0，对目标xT＝40km，50km，60km分别进行仿真计算，LG节点个数取为35，优化算法工具包为SNOPT，仿真结果如图1～图5所示。

从图1可见，制导炮弹在经过弹道最高点后，近乎以直线滑翔，当快达到末端时，弹道开始俯冲，这是由于为了保证最后的攻击效果，对末端条件进行约束所致。图2描述了滑翔过程中速度的变化规律，可以发现，速度在中间阶段变化非常缓慢，但当接近弹道末端时开始衰减，这是因为弹丸在末段以较大的负攻角进行俯冲，增大了飞行阻力，因此速度衰减较快。

图1 不同射程情况下的弹道曲线

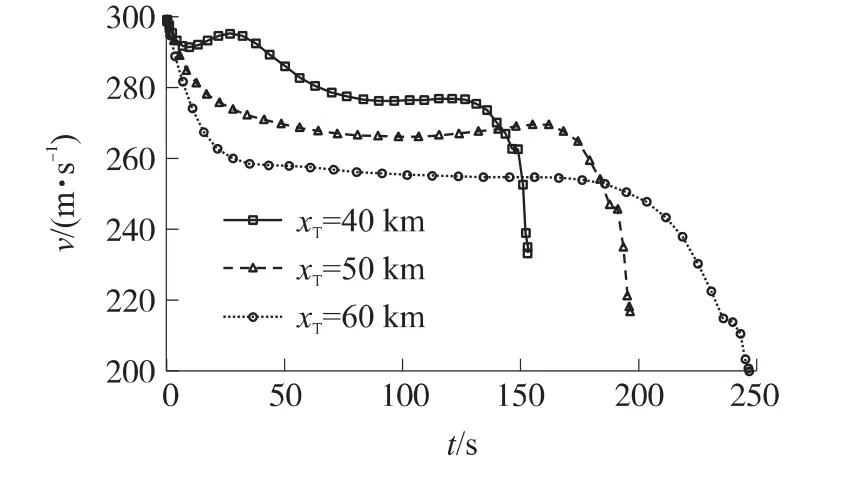
图2 不同射程情况下的速度曲线

图3 也很明显地反映出弹道倾角在经过短暂的减小后，在较长的时间内近乎保持不变，验证了弹丸近似直线飞行，当接近弹道末端时，弹道倾角先增加后急剧减小，说明弹丸开始俯冲，且最终落角均大于89°，满足设计指标。

图3 不同射程情况下的弹道倾角曲线

图4 为不同射程条件下虚拟控制量uα和实际控制量αB的对比曲线，可以看出，因为考虑了动力学滞后，为了使攻角迅速增加，uα在初始时刻的值较大，之后慢慢减小，逐渐与αB重合。由于在构建优化模型时对末端弹道倾角进行了约束，｜θ（tf）｜≥θf，为了满足这种约束，升力需在弹道末端变为负值，根据升力计算公式，此时攻角也应该为负值，且θf越大，攻角的绝对值也越大，从而攻角曲线在末端出现了图4所示的陡峭现象。此外，由于动力学滞后的存在，uα在末端的下降过程中要超前于αB。

图4 不同射程情况下的实际控制量和虚拟控制量曲线

图5 展示了考虑动力学滞后的攻角改善效果。可以明显地看出，考虑动力学滞后的攻角变化较为平缓，以xT＝60km为例，不考虑动力学滞后时，攻角在初始时刻从0瞬间增加到接近6°，这种突变往往会给今后控制系统的准确跟踪带来较大的困难。而在考虑动力学滞后时，这种现象便不再出现，优化得到的攻角曲线变化非常平缓。

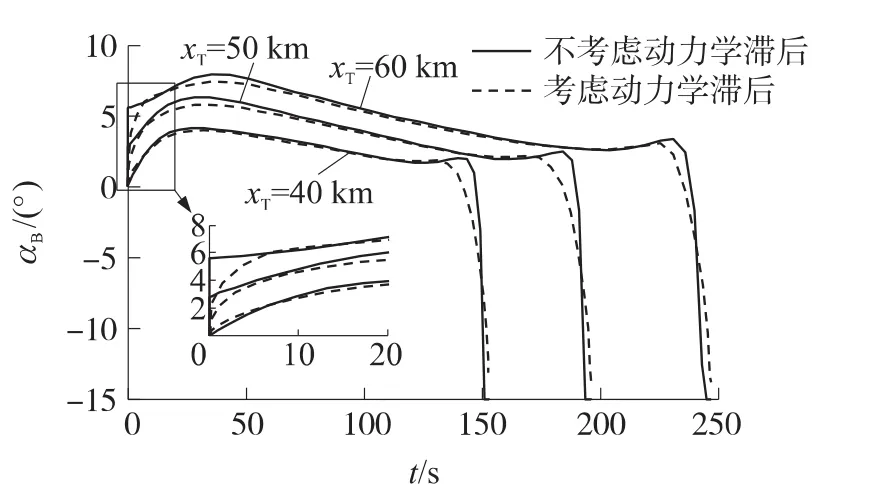
图5 考虑动力学滞后攻角改善效果

为了进一步验证Gauss伪谱法的高效性，利用直接打靶法［14］在同样的计算平台上分别对xT＝40km，50km，60km的弹道进行了优化计算，离散控制量所需的节点设置为均匀分布，且个数取为35，积分步长取为0.5s，对于优化模型中的各种约束，采用罚函数法进行处理，优化结果对比见表1。从中可看出，直接打靶法优化出的弹道飞行时间大于Gauss伪谱法，这说明其寻优效果要低于Gauss伪谱法。此外，直接打靶法的优化结果并没有完全满足落角约束，可见，在终端位置、速度和落角等诸多约束的条件下，相比于Gauss伪谱法，直接打靶法的精度有所欠缺。最后，直接打靶法的优化耗时tcost要远大于Gauss伪谱法，这是因为直接打靶法在每次迭代时都会利用控制量积分弹道，虽然选取了较大的积分步长（0.5s），但是大量的迭代还是产生了巨大的计算耗时，明显地降低了算法的效率，而Gauss伪谱法无需在每次迭代中积分弹道，因此在计算效率上具有很大的优势。图6为两种方法优化得到的攻角的对比图，从中可看出二者基本吻合，但Gauss伪谱法的结果要更为光滑。从以上的分析可以看出，Gauss伪谱法不论在优化效率还是精度上均强于直接打靶法。

表1 直接打靶法和Gauss伪谱法优化结果对比

图6 直接打靶法和Gauss伪谱法攻角对比曲线

4 结束语

本文基于Gauss伪谱法求解了远程制导炮弹滑翔弹道快速优化问题。以快速精确打击为指标对滑翔弹道进行了优化设计，考虑动力学滞后，引入虚拟控制量，并将其作为优化变量，在纵向平面内建立了弹道优化模型；利用Gauss伪谱法将优化模型在一系列LG节点上离散，将连续的无限维最优控制问题转换为一般的非线性规划问题。仿真结果表明，弹丸能以一定的速度和大着角攻击目标，所有约束条件均能较好地满足，引入虚拟控制量后，优化得到的攻角曲线更为平滑。与传统的直接打靶法相比，Gauss伪谱法计算时间短，优化效率高，具有在线优化的潜力，促进了制导炮弹快速精确打击、及时火力支援等能力的有效发挥，可为远程制导炮弹的方案弹道优化设计提供一定的参考。

［1］COSTELLO M.Extended range of a gun launched smart projectile using controllable canards［J］.Journal of Guidance，Control，and Dynamics，2006，29（6）：1 404－1 414.

［2］COSTELLO M.Extended range of a gun launched smart projectile using controllable canards［J］.Journal of Shock and Vibration，2001，8：203－213.

［3］史金光，王中原，易文俊.滑翔増程弹方案弹道特性研究［J］.弹道学报，2003，15（1）：51－54.SHI Jin－guang，WANG Zhong－yuan，YI Wen－jun.A study on the projectile trajectory characteristics of gliding extended range projectile［J］.Journal of Ballistics，2003，15（1）：51－54.（in Chinese）

［4］史金光，王中原，易文俊.滑翔増程弹飞行弹道［J］.火力与指挥控制，2007，32（11）：88－90.SHI Jin－guang，WANG Zhong－yuan，YI Wen－jun.Study of fight trajectory for gliding extended range projectile［J］.Fire Control and Command Control，2007，32（11）：88－90.（in Chinese）

［5］卜奎晨，刘莉.复合制导炮弹最优滑翔弹道与控制［J］.弹道学报，2007，19（4）：23－25.BU Kui－chen，LIU Li.Optimal glide trajectory and control for combined guidance munition［J］.Journal of Ballistics，2007，19（4）：23－25.（in Chinese）

［6］汪小娜，王树宗，朱华兵.火箭助推滑翔増程炮弹弹道模型研究［J］.舰船科学技术，2005，27（1）：77－79.WANG Xiao－na，WANG Shu－zong，ZHU Hua－bing.Study on ballistic models of rocket－aid gliding extended projectiles［J］.Ship Science and Technology，2005，27 （1）：77 － 79.（in Chinese）

［7］易文俊，王中原，史金光，等.带鸭舵滑翔増程炮弹方案弹道研究［J］.南京理工大学学报，2008，32（3）：322－326.YI Wen－jun，WANG Zhong－yuan，SHI Jin－guang.Trajectory of glide extended－range projectile with canards configuration［J］.Journal of Nanjing University of Science and Technology，2008，32（3）：322－326.（in Chinese）

［8］史金光，王中原，涂泗华.求解滑翔増程弹较优舵偏角方法［J］.弹箭与制导学报，2005，25（4）：717－719.SHI Jin－guang，WANG Zhong－yuan，TU Si－hua.Calculating method on a suitable angle of lift－canards of gliding extended range projectile［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2005，25（4）：717－719.（in Chinese）

［9］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京：北京理工大学出版社，2008.QIAN Xing－fang，LIN Rui－xiong，ZHAO Ya－nan.Missile flight dynamics［M］.Beijing：Beijing Institute of Technology Press，2008.（in Chinese）

［10］BENSON D.A Gauss pseudospectral transcription for optimal control［D］.Cambridge：Massachusetts Institute of Technology，2005.

［11］关冶，陆金甫.数值分析基础［M］.北京：高等教育出版社，2005.GUAN Ye，LU Jin－fu.Fundamentals of numerical analysis［M］.Beijing：High Education Press，2005.（in Chinese）

［12］GILL P E，MURRAY W，SAUNDERS M A.SNOPT：an SQP algorithm for large－scale constrained optimization［J］.SIAM Review，2005，47（1）：99－131.

［13］ACHTER A W，BIEGLER L T.On the implementation of a primal－dual interior point filter line search algorithm for largescale nonlinear programming［J］.Mathematical Programming，2006，106（1）：25－57.

［14］GERDTS M.Direct shooting method for the numerical solution of higher－index DAE optimal control problems［J］.Journal of Optimization Theory and Applications，2003，17（2）：267－294.