空域窗射击参数自寻优设计与实现
单甘霖,刘 恒,梅 卫
(军械工程学院 电子与光学工程系,石家庄,050003)
高炮系统是近程末端防御武器系统的重要组成部分。传统上,高炮通常采用集火射击目标提前点的方式拦截空中目标。随着空袭目标机动性能的不断提升,火控系统所作的运动假定难以与其实际航迹相吻合,这就导致预测提前点的精度下降。为弥补集火射击的不足,国外于20世纪80年代提出了一种新型的火力控制方法——未来空域窗射击体制[1]。它通过在预测未来点的近旁建立弹丸或破片具有近似均匀散布特性的空中区域,尽可能覆盖作有限机动的目标,但国外关于该技术的公开文献资料很少。国内南京理工大学等单位[1-7]从20世纪90年代开始开展了相关研究,取得了一些成果,但对该体制中的空域窗射击参数(大小和形状)这一关键问题缺乏定量研究,使得运用该技术的高炮系统射击效果往往不是全局最优的。文献[1]提出了以预测迎弹面内弹头近似均匀散布为依据的未来空域窗设计方法,忽略了实际中的随机穿越特性。该方法特点是能够以较少的弹丸数毁伤位置预测精度较高的目标;文献[2]从随机穿越特性入手,提出了根据目标位置预测误差方差来设计空域窗参数的方法。该方法设计的未来空域窗具有较好的随机穿越特性,可使目标较长时间地滞留在窗内;文献[3]从随机穿越特性和弹丸散布密度两方面综合考虑,分别提出了跟踪射击模式和拦阻射击模式下的设计方法。
本文以目标的运动特征参数为依据,考虑典型高炮武器系统性能参数,提出基于毁歼目标的概率最优自适应设定空域窗射击参数的算法。首先将文献[8]中介绍的集火射击毁歼概率计算模型加以改进,构建空域窗射击毁歼概率计算模型;然后选择模式搜索法求解空域窗射击参数的最优值;最后通过仿真验证选择模式搜索法的可行性。
1 空域窗射击毁歼概率计算模型
文献[8]介绍的“着发射击高炮系统毁歼概率计算模型”仅适用于集火射击。本文对此模型加以改进,拓展其应用范围,使之适用于空域窗射击体制。把改进后的模型称为空域窗射击毁歼概率计算模型,然后基于优化算法求解该模型,即可得到最优的空域窗射击参数,故此模型是计算空域窗射击参数的基础。
构建模型过程中使用2个空间坐标系(右手系),如图1所示。

图1 建模中的坐标系
①直角坐标系。坐标原点为炮口位置O,过O点作平行于水平面的平面,称为炮口水平面Z。取X轴正向为正东方向,Y轴正向为正南方向,H轴正向为垂直向上的方向。则坐标系中目标位置M由坐标(x,y,h)确定。
②射击误差坐标系[8]。假设在弹丸命中目标的时刻t,目标位于Mq点。过Mq点作一个垂直于炮目连线OMq的平面Q,称之为预测迎弹面。在Q平面上建立坐标系Mq-X1X2,其中,X1轴为过炮目连线OMq的铅垂面与平面Q的交线,正向朝上;X2轴与X1轴垂直,正向与航路方向同侧。
假设空域窗形状的长、短轴方向分别与预测迎弹面上方向、高低误差方向一致。如图2所示,空域窗射击与集火射击的本质区别在于:集火射击时各弹丸散布中心Di,i=1,2,…,m(m是弹丸散布中心个数,通常一门高炮对应一个弹丸散布中心)与Mq点一致,即各高炮均指向Mq点射击,其系统误差大小一致;空域窗射击时其窗内各弹丸散布中心Di与Mq点不重合,而是均匀分布在以Mq点为圆心的圆周或椭圆周上,各高炮不再指向Mq点射击,而是指向各自的弹丸散布中心Di,即各高炮的系统误差大小不一致,需分别计算。
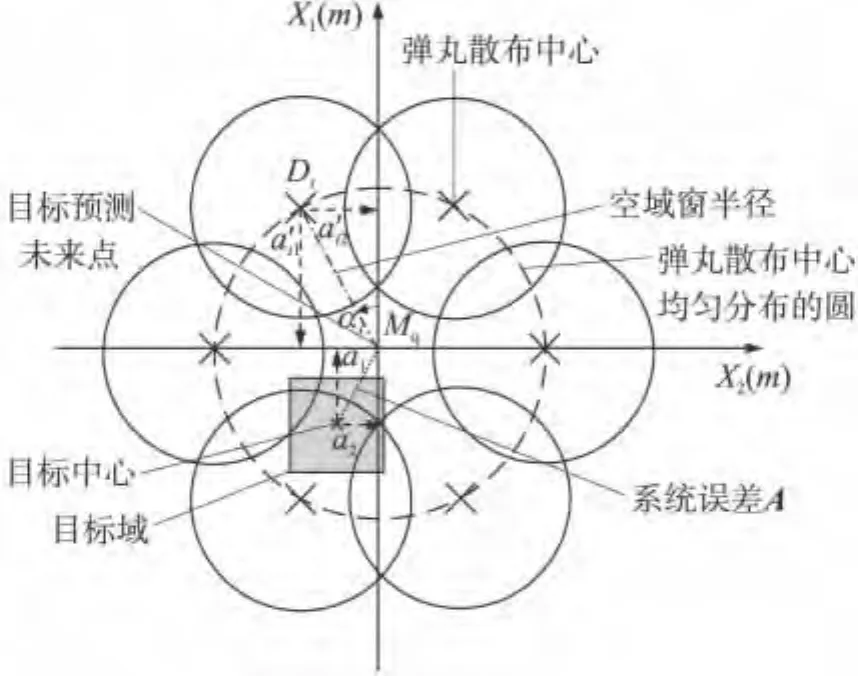
图2 原理图
假设集火射击时Mq离目标中心的系统误差为A,可分解为A=(a1a2)。根据空域窗射击原理,第i个弹丸散布中心Di相对Mq的偏差A′i分解为A′i=(a′i1a′i2),则Di相对目标中心的系统误差ΔA′i为:ΔA′i=(a1-a′i1a2-a′i2),其中,偏差A′i通过3个参数ra,rb,αi表征:

式中:rb,ra分别为弹丸散布圆短、长半轴,记为空域窗的射击参数。若ra=rb,则空域窗为圆形,否则,空域窗为椭圆。α0是第1个弹丸散布中心D1与X1轴正向之水平夹角,它服从上的均匀分布。
则未来空域窗体制下的毁歼概率计算模型为

式中:l是目标投影等效矩形边长的一半,Φ是文献[8]中提出的单门高炮集火射击毁歼概率计算模型,Pkill是空域窗射击的毁歼概率。
综上所述,空域窗射击毁歼概率计算模型的基本思想是:先分别计算武器系统内各高炮(一门高炮对应一个弹丸散布中心)的系统误差ΔA′i,然后利用单门高炮集火射击毁歼概率计算模型求解出各高炮对应的毁歼概率值。最后,把系统内所有高炮的毁歼概率值求和,即为空域窗射击毁歼概率。
2 基于模式搜索法的模型求解算法
空域窗射击参数自寻优设计的目的是寻找最佳的射击参数(rb,ra),使毁歼目标的概率最大。建立如下数学模型:
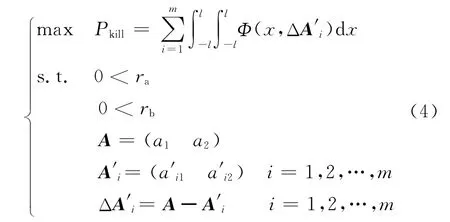
构建出数学模型后,下面研究求解模型的算法。目前,传统的优化算法和智能算法有很多种[9]。分析文中所研究的问题可知,火控诸元解算时主要的评价指标是诸元精度和实时性,并且对实时性这个指标的要求更高,故在选择优化算法时需要对这2个指标综合考虑。
通过对空域窗射击毁歼概率计算模型的分析,发现该模型并不存在多个极值点,这样在求解模型时就不会遇到陷入局部最优的问题;但同时由于此模型计算过程中涉及的公式较多,比较复杂,不容易用解析法直接获得其导数等信息。通过综合比较各优化算法的性能,选择模式搜索法进行模型解算。
模式搜索法由Hooks和Jeeces(1961年)提出,它并不需要任何目标函数的梯度信息[9-11],适合解决文中所提的问题。它由“探测性”移动和“模式性”移动组成。前者是以一定的步长沿着轴向探索,揭示目标函数的变化规律,探测函数的下降方向;后者则是在此基础上沿着有利方向直接搜索,寻找更好的点[11]。
3 仿真与分析
选取典型航路点进行仿真实验,先通过枚举法分析空域窗最优射击参数的存在性问题,在确定该参数唯一存在后,将其作为最优解,与模式搜索法等其它优化算法的计算结果进行比较,分析选择模式搜索法的可行性。
仿真条件:高炮系统性能参数见文献[8]第6.2节,其余参数如下。
第1组数据:目标提前点位置坐标为xq=500m,yq=400m,hq=100m;提前点位置预测误差均方差为σx=2m,σy=5m,σh=1m。
第2组数据:xq=500m,yq=400m,hq=100m;σx=2m,σy=8m,σh=1m。
第3组数据:xq=1 500m,yq=400m,hq=500m;σx=2m,σy=5m,σh=1m。
①仿真一:分析空域窗最优射击参数的存在性。
选择第1组仿真数据,通过枚举法计算各点的毁歼概率值,然后选择出毁歼概率最大值,与此值相对应的空域窗射击参数即为最优解。
仿真时为方便观察目标函数的变化规律,此处取其为毁歼概率相反数P′kill。仿真结果如图3所示。图3(a)为空域窗短半轴rb取[0,8]m、长半轴ra取[7,20]m时的目标函数变化规律图;图3(b)为目标函数曲面等高线图,与目标函数最小值对应的横、纵轴取值即为最优的空域窗射击参数。通过图3可知,在此组仿真条件下,最优的空域窗射击参数取值rb=4.1m,ra=12.3m,与之对应的毁歼概率值Pkill=0.960 4。这说明,空域窗射击毁歼概率计算模型存在最优解。另外2组仿真条件下的仿真结果分别为:第2组最优解为:rb=3.4m,ra=19.2m,毁歼概率值Pkill=0.899 3;第3组最优解为:rb=1.3m,ra=12.9m,毁歼概率值Pkill=0.541 8,具体过程不再赘述。
将此节3种仿真条件下得到的最优解作为基准值,检验模式搜索法等其它优化算法的性能。
②仿真二:模式搜索法与其它优化算法性能比较。
由于不容易直接比较射击参数的优劣,选择计算耗时及与射击参数相对应的毁歼概率计算精度2个指标,对各算法的性能进行比较。表1中的模拟退火算法、遗传算法和极小化极大值算法来源于Matlab中现有函数,仿真结果如表1所示。

图3 不同参数下的毁歼概率

表1 仿真数据
结果分析:
①仅比较毁歼概率Pkill的计算精度这个指标,3种仿真条件下,4种算法由好到差的排列顺序都是:模拟退火算法→遗传算法→模式搜索算法→极小化极大值算法;同理,仅比较计算耗时指标t耗时由少到多,排列顺序是:模式搜索算法→极小化极大值算法→遗传算法→模拟退火算法。可以看出,模拟退火算法的高精度是以庞大的计算耗时为代价的;极小化极大值算法计算精度不如模式搜索法,且耗时也更长;虽然遗传算法的计算精度比模式搜索法略有提高(3种仿真条件下分别为0.36%、0.26%和0.32%,均值仅为0.31%),但耗时要长。综合比较4种优化算法,模式搜索法是最合适的。
②与毁歼概率最大值相比,3种仿真条件下模式搜索法计算结果的相对误差分别是0.60%、0.30%和0.74%,它们的均值为0.55%,可见两者相差不大。这表明模式搜索算法的计算精度同样可以接受,可以作为次优解;虽然模式搜索算法的计算精度不是最高的,但其实时性却是最好的,比其它算法的计算量显著降低,这说明该算法更具有实用性,故针对本文中的问题,选择模式搜索算法是可行的。
4 结论
本文从空域窗射击参数的优化设计问题出发,研究目标运动状态与空域窗射击参数的关系,优化了一次毁歼概率;构建了未来空域窗射击毁歼概率计算模型,并提出选择模式搜索算法求解空域窗射击参数。仿真结果表明,该方法在计算精度降低0.55%的同时,大幅度减少了计算耗时,是可行有效的。
[1]胡金春,郭治.未来空域窗的数学描述[J].兵工学报,1998,19(4):293-297.HU Jin-chun,GUO zhi.Mathematical description of future airspace window[J].Acta Armamentarii,1998,19(4):293-297.(in Chinese)
[2]胡金春,郭治.未来空域窗的参数论证.[J]兵工学报,1999,20(1):13-18.HU Jin-chun,GUO zhi.On the optimisation of parameters for future airspace window[J].Acta Armamentarii,1999,20(1):13-18.(in Chinese)
[3]吕学新.未来空域窗应用技术[D].南京:南京理工大学,2007.LV Xue-xin.Technology of future airspace window[D].Nanjing:Nanjing University of Science & Technology,2007.(in Chinese)
[4]窦丽华,王高鹏,陈杰,等.求解弹头散布均匀度的分布估计算法[J].控制理论与应用,2009,26(6):624-628.DOU Li-hua,WANG Gao-peng,CHEN Jie,et al.A hybrid algorithm for computing cannonball dispersion evenness [J].Control Theory & Applications,2009,26(6):624-628.(in Chinese)
[5]刘恒,梅卫,卢大庆,等.自适应射击窗火力控制技术研究[J].火力与指挥控制,2012,37(10):70-73.LIU Heng,MEI Wei,LU Da-qing,et al.Fire control technology featured on adaptive shooting window[J].Fire Control & Command Control,2012,37(10):70-73.(in Chinese)
[6]孙世岩,邱志明,王航宇,等.拦阻面弹丸散布中心配置方法[J].弹道学报,2008,20(4):16-19.SUN Shi-yan,QIU Zhi-ming,WANG Hang-yu,et al.Dispersion center configuraion method of barrage firing curtain[J].Journal of Ballistics,2008,20(4):16-19.(in Chinese)
[7]梅卫,王春平,程远增.基于多模射击的火力控制理论研究[J].火力与指挥控制,2009,34(2):101-103.MEI Wei,WANG Chun-ping,CHENG Yuan-zeng.Fire control theory based on multible mode shooting[J].Fire Control &Command Control,2009,34(2):101-103.(in Chinese)
[8]肖元星,张冠杰.地面防空武器系统效费分析[M].北京:国防工业出版社,2006:139-205.XIAO Yuan-xing,ZHANG Guan-jie.Effectiveness cost analysis on land-based air defense weapon system[M]BeiJing:National Defense Industry Press,2006:139-205.(in Chinese)
[9]谢政,李建平,陈挚.非线性最优化理论与方法[M].北京:高等教育出版社,2010:206-210.XIE Zheng,LI Jian-ping,CHEN Zhi.Nonlinear optimization theory and methods[M].Beijing:Higher Education Press,2010:206-210.(in Chinese)
[10]WU T,SUN L P.A filter-based pattern search method for unconstrained optimization[J].Numerical Mathematics,2005,15(3):209-216.
[11]韩丽霞,王宇平,兰绍江.基于模式搜索的类电磁算法求解约束优化问题[J].系统工程与电子技术,2009,31(9):2 219-2 222.HAN Li-xia,WANG Yu-ping,LAN Shao-jiang.Electromagnetismlike method based on pattern search for constrained optimization problem[J].Systems Engineering and Electronics,2009,31(9):2 219-2 222.(in Chinese)

