基于在线修正弹道模板的主动段弹道跟踪方法
郭 跃,刘新学,蒋 鸣
(1.第二炮兵工程大学 初级指挥学院,西安 710025;2.第二炮兵装备研究院,北京 100089)
弹道导弹在主动段不存在机动变轨等突防措施,而且弹道变化单一[1],因此拦截处于主动段的弹道导弹的作战效果十分明显。对主动段弹道导弹的准确跟踪和定位是拦截主动段弹道导弹的重要一环[2-3]。申镇[4]等基于运动方程对单星无源的主动段弹道射向进行了估算,张涛、安玮[5-7]等给出了基于推力加速度模板的主动段跟踪算法,但是需要获得主动段的推力加速度信息。陈映和程臻等[8-9]给出了一种参变量助推弹道导弹时不变运动模型,但也是基于情报数据库为先验知识,同时还认为导弹主动段的运动模型可以用加加速度模型来近似计算,并采用交互多模型(interacting multiple model,IMM)的不敏卡尔曼滤波(IMM-UKF)算法进行了仿真。Li X R和Jilkov V P给出了全弹道的跟踪模型和滤波模型,将主动段的跟踪模型简化为变加速度模型或重力转弯模型,但与导弹主动段实际的运动模型相比还存在较大差异[10-12]。本文从弹道导弹主动段的实际运动模型入手,建立了一种基于在线修正的主动段弹道跟踪模型,该模型可以对导弹参数进行在线估计,也可用于离线弹道导弹参数的采集。
1 在线修正主动段弹道模板
设地基雷达坐标系定义与NUE(North-Up- East)坐标系相同,坐标原点经、纬度及当地高程为(φr0,λr0,hr0),则从地基雷达坐标系到地心直角坐标系(earth right angle coordinate system)的转换矩阵为
(1)
如图1所示,图中,Fp为导弹推力,θtra为推力方向与轨迹坐标系x轴的夹角,FR为总空气动力,θR为总空气动力与轨迹坐标系x轴的夹角。AT为射面与北向的夹角,θg为导弹在雷达坐标系中的矢径与其在OradarXradarYradar平面内投影的夹角。在主动段的跟踪过程中应选择轨迹坐标系来描述,其原点Otraj为导弹质心,OtrajXtraj轴与导弹速度方向一致,OtrajYtraj位于射击平面内且垂直于OtrajXtraj,OtrajZtraj符合右手定则。
因此轨迹坐标系到雷达坐标系的转换矩阵为
1.1 重力模型
设t时刻导弹在雷达坐标系的位置为(xrmyrmzrm)T,则导弹所受引力加速度为[1]
式中:grx,gry,grz分别为重力在雷达坐标系内的各轴的分量;Gm为地心引力常数;rm为导弹在地心直角坐标系内的距离;ω为地球自转角速度;B0为发射点大地纬度;φs为导弹在(xrmyrmzrm)T所对应的地心纬度;R0,rx,R0,ry,R0,rz分别为雷达坐标系原点的地心矢径在雷达坐标系各轴的分量;μ为地球扁率系数;a,e1,αe分别为椭球地球体长半轴,偏心率和地球扁率;(ωrxωryωrz)T为地球自转角速度在雷达坐标系内的向量表示。
1.2 科氏力和牵连惯性力模型
科氏加速度arc在雷达坐标系的投影为
牵连加速度are在雷达坐标系的投影为
(7)
式中:vrmx,vrmy,vrmz分别为导弹速度在雷达坐标系内各轴向的分量;ωrx,ωry,ωrz分别为地球自转角速度在雷达坐标系内各轴向的分量。在弹道导弹目标的跟踪过程中,由科氏力和牵连力引起的位置跟踪误差会随着时间不断累积,对洲际弹道导弹(ICBM)而言主动段飞行时间在几百s以上,因此在对主动段飞行的导弹建模时应考虑科氏力和牵连力对导弹加速度的影响。
1.3 空气动力模型
导弹主动段气动力的计算由于涉及导弹姿态、气动力系数以及飞行程序角等,因此,在计算导弹气动力时所建立的六自由度空气动力模型不仅参数多、模型复杂,而且估算也很难准确。
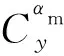

1.4 推力模型和导弹质量模型
设i为导弹的级数,一般i小于3级,导弹的实时质量可表示为
(9)

推力FP在主动段对导弹作用力最大,因此可以通过加速度大小的变化准确推算出导弹发动机是否工作,这样对导弹当前质量m(tc)的估计就变为与导弹前一时刻的质量m(tc-1)及常数C有关。
主动段导弹的推力公式为
FP(t)=FP0,i-Se(p0-pH)=FP0,i-ΔFP
(11)
式中:FP0,i为第i级的地面额定推力,Se为主动段发动机横截面积,p0为地面的大气压,pH为高度H的大气压。多级火箭各级推力不同,主动段导弹推力的大小可以视为由地面额定推力FP0和由大气压强引起的推力变化ΔFP共同决定。
推力加速度矢量表示为
arP=FP(t)/m(t)
(12)
在射面内推力FP(t)可以视为
式中:θP为推力FP(t)与速度方向的夹角,ΔFP为推力的变化量。因此推力FP(t)的估算就变为对FP0,θP,ΔFP的估算。
1.5 总的加速模板模型
导弹在主动段的加速度方程可以表示为
am=arP+ara+arc+are+gr
(13)
式中的加速度gr,are,arc可以根据上述模型准确地计算,推力引起的加速度arP,空气动力引起的加速度ara是预测的难点。
2 基于交互多模型算法的主动段弹道跟踪
2.1 主动段弹道跟踪模型
1)加加速度模型(Jerk)[2-3,7]。
陈映等通过研究多种不同类型弹道导弹的加速度随时间的变化曲线,认为在主动段导弹的加速度近似为线性,而将加加速度近似为常数。主动段的状态向量可以表示为

主动段导弹跟踪的Jerk模型为
Xr(k+1)=AXr(k)+W(k)
(15)
式中:T为探测周期,A为转换矩阵,W(k)为噪声干扰。
2)当前统计模型(CSM)。
导弹在主动段所受重力、科氏力、牵连惯性力可以通过计算获得,而推力和空气动力很难有准确的模型进行跟踪,因此对推力和空气动力引起的加速度可以视为修正的瑞利马尔科夫过程。选择系统的状态变量:
Xr=(xryrzrvrxvryvrzarxaryarz)T
(17)
W(t)=(O1×6ωPax(t)ωPay(t)ωPaz(t))T
(21)

2.2 IMM算法的实现
IMM算法是一种动态多模型算法,通过设计和建立多种弹道导弹模型的主动段跟踪模型来构造IMM算法是提高导弹跟踪精度的有效手段[8,11]。本文根据弹道导弹主动段的运动特点选择了CS模型和Jerk模型作为跟踪模型,同时结合不敏卡尔曼滤波(unscented Kalmar filter,UKF)和不敏粒子滤波(unscented particle filter,UPF)算法构建了IMM-UKF-UPF算法。算法流程图如图2所示。

图2 IMM-UKF-UPF算法流程图
CS和Jerk跟踪模型同前,UKF和UPF算法的实现,限于篇幅,不做赘述。
3 弹道模板参数的解算和仿真研究
基于弹道模板的算法一方面可以通过对弹道的量测获得弹道相关参数,另一方面在实际的测量过程中可以为弹道预测提供参考依据。算法如图3所示。图中,Isp为导弹发动机的比冲。

图3 基于弹道模板的算法结构图
对弹道采用四阶Runge-Kutta法进行解算。
设k时刻导弹加速度滤波后的矢量为

写出k和k+1时刻的向量展开式:


以2级洲际导弹TD2为模型进行算法的仿真验证[12],其在雷达坐标系内各参数的变化情况如图4~图7和表1所示。
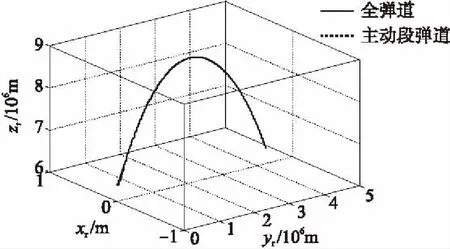
图4 主动段在全弹道中的示意图
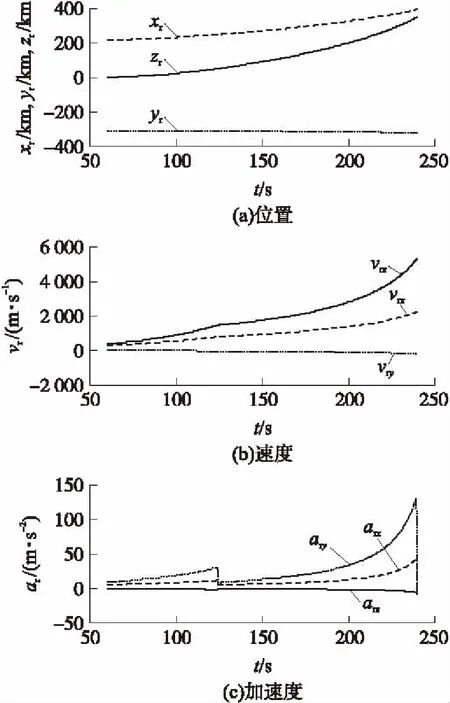
图5 雷达探测的主动段各参数随时间的变化

图6 解析方法对主动段各力的估算结果分析
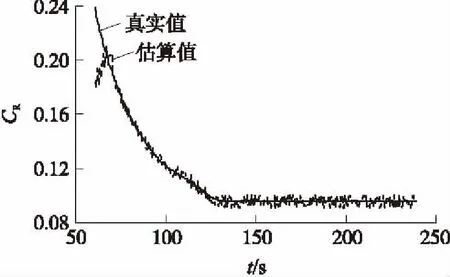
图7 空气动力系数的估算情况分析


表1 基于弹道模板的各常值参数的估算
把估算参数得出的在线修正的弹道跟踪模型(ONPT)与交互多模型方法(IMM)分别结合UPF和UKF算法进行滤波,仿真结果如图8、图9所示。

图8 OLPT与IMM算法跟踪导弹位置均方差比较图

图9 OLPT与IMM算法跟踪导弹速度均方差比较
从仿真结果来看,基于在线修正弹道模板的主动段弹道跟踪方法能够对弹道导弹的各常值参数进行准确的估计,同时对动态变化的参数也能进行比较好的跟踪,但是导弹级间转换时(如图6)对推力和发动机质量流量的跟踪稍显滞后。该方法可以用于平时弹道导弹数据的采集和分析并构建准确的弹道模板,也可以对导弹进行在线跟踪。在对导弹进行跟踪的过程中,基于在线修正的弹道模板(ONPT)方法与交互多模型(IMM)方法相比有着更好的跟踪精度,显然导弹模板的参数越准确跟踪效果越好。
[1] 张毅,杨辉耀,李俊莉.弹道导弹弹道学[M].长沙:国防科大出版社,1999:111-157.
ZHANG Yi,YANG Hui-yao,LI Jun-li.The ballistic trajectory[M].Changsha:National University of Defense Technology Press,1999:111-157.(in Chinese).
[2] 郭尊华,谢维信.弹道导弹跟踪技术进展[J].信号处理,2009,25(8a):578-581.
GUO Zun-hua,XIE Wei-xin.Ballistic missile tracking:a review[J].Signal Processing,2009,25(8a):578-581.(in Chinese)
[3] 周宏仁,敬忠良,王培德.机动目标跟踪[M].北京:国防工业出版社,1991.
ZHOU Hong-ren,JING Zhong-liang,WANG Pei-de.Mobile target tracking[M].Beijing:National Defense Industry Press,1991.(in Chinese)
[4] 申镇,强胜,易东云.基于运动方程的单星无源主动段射向估计方法[J].弹道学报,2010,22(1):7-10.
SHEN Zhen,QIANG Sheng,YI Dong-yun.Course head estimation method based on movement equation by single satellites passive detection in boost phase[J].Journal of Ballistics,2010,22(1):7-10.(in Chinese)
[5] 张涛,安玮,周一宇,等.基于推力加速度模板的主动段弹道跟踪方法[J].宇航学报,2006,27(3):385-389.
ZHANG Tao,AN Wei,ZHOU Yi-yu,et al.Periodic relative motion condition for satellites formations considering nonlinearity[J].Journal of Astronautics,2006,27(3):385-389.(in Chinese)
[6] 张涛,安玮,周一宇.基于UKF的主动段弹道跟踪算法[J].弹道学报,2006,18(2):15-18.
ZHANG Tao,AN Wei,ZHOU Yi-yu.Trajectory tracking method in boost phase by using UKF[J].Journal of Ballistics,2006,18(2):15-18.(in Chinese)
[7] 张涛,安玮,周一宇.主动段弹道定位与跟踪算法[J].弹道学报,2005,17(4):11-16.
ZHANG Tao,AN Wei,ZHOU Yi-yu.The trajectory locating and tracking algorithm in boost phase[J].Journal of Ballistics,2005,17(4):11-16.(in Chinese)
[8] 陈映,程臻,文树梁.弹道导弹助推段同时跟踪和类型识别算法研究[J].信号处理,2011,27(5):749-754.
CHEN Ying,CHENG Zhen,WEN Shu-liang,Study on method for simultaneously tracking and classifying ballistic missile in boost and post-boost phase[J].Signal Processing,2011,27(5):749-754.(in Chinese)
[9] 陈映,文树梁,程臻.一种适用于助推段弹道导弹的跟踪方法研究[J].系统仿真学报,2012,24(5):1 063-1 067.
CHEN Ying,WEN Shu-liang,CHENG Zhen.Method for tracking ballistic missile on boost phase[J].Journal of System Simulation,2012,24(5):1 063-1 067.(in Chinese).
[10] LI X R,JILKOV V P.A survey of maneuvering target tracking,part Ⅱ:ballistic target models[J].SPIE,2001,4 473:559-581.
[11] LI X R,JILKOV V P.A survey of maneuvering target tracking,part Ⅲ:measurements models[J].SPIE,2001,4 473:423-446.
[12] JOHN A,LUKACS I V.Hit-to-kill guidance for the interception of ballistic in the boost phase[D].Monterey,CA:Naval Postgraduate Shool,2006.

