旋转控制固定鸭舵二维弹道修正弹气动特性

吴 萍,陈少松,杨晋伟,谭献忠,杜学伟

(1.南京理工大学 能源与动力工程学院,南京 210094;2.淮海工业集团有限公司,山西 长治 046012)

远程精确打击是现代武器装备发展的方向,导弹是精确打击武器的代表。导弹可以远程发射并直接对目标予以毁灭性的打击,但是它的造价昂贵,无法大规模装备使用[1]。弹道修正弹通过加装低成本的修正机构,对原本无控飞行的弹道进行修正,提高弹箭射击密集度,实现精确打击。弹道修正弹特别适合于远程弹箭,通过改进原有引信,加装修正机构,即可达到对原本无控弹箭进行精确化改进的目的,具有成本低、精度高、性价比高的优点[2]。

弹道修正是在弹箭飞行弹道的合适位置,通过修正机构的作用改变弹箭的气动外形以改变气动力,进而对弹箭的飞行弹道进行修正,提高射击密集度。弹道修正弹分为一维弹道修正弹和二维弹道修正弹。一维弹道修正弹通过增加纵向的气动阻力来实施对射程的改变,达到提高射击纵向密集度的目的。早在1994年,美国陆军装备研究发展与工程中心(ARDEC)就开始推进基于GPS定位的自动修正阻力器式(一维距离修正式)和制导式(距离和方向二维修正式)引信的研究工作;二维弹道修正弹不仅要改变纵向气动力,还要改变横向气动力,实现对弹箭纵向距离和横向偏差的修正,提高纵横向的密集度指标[3]。2003年美国陆军就提出二维弹道修正引信的采购项目,即XM1156式精确制导组件(PGK)的低成本弹道修正引信采购项目,加装该二维弹道修正引信的二维修正弹预期要达到圆概率误差50 m的水平[4]。针对高速旋转榴弹,有一种二维修正机构采用鸭舵修正机构,该鸭舵偏角固定,如图1所示,2对舵中一对舵呈俯仰偏航姿态,另一对舵呈差动姿态。俯仰偏航舵修正弹丸纵向距离和横向偏差;差动舵控制修正机构旋转,控制俯仰偏航舵所处的位置。该种二维弹道修正弹称为旋转控制固定鸭舵二维弹道修正弹。关于这种结构二维弹道修正弹的气动力研究所见报道很少,文献[5-6]采用数值模拟的方法对此种类型的全弹气动力和鸭舵修正气动力进行了研究。

图1 XM1156式精确制导组件(PGK)

本文采用风洞实验研究方法,对该弹在亚跨超音速时不同舵偏角下俯仰气动特性、滚转气动特性、升阻比的气动特性进行了研究,得到了各气动参数随马赫数、攻角和舵偏角的变化规律,为这种弹的弹道设计和研究提供了参考依据。

1 风洞及实验模型

本实验是在某HG-4号风洞中进行的。HG-4号风洞为直流下吹暂冲式闭口高速风洞,实验段截面为300 mm×300 mm,实验段长为600 mm。

实际飞行过程中,差动舵差动方向与弹的旋转方向相反,起到旋转刹车的作用,最终使得差动舵和俯仰舵组成的修正头部与弹体隔转,即该部分相对大地坐标系不转。当需要进行纵向修正时,俯仰舵处于水平位置,向上或向下打舵使弹增加或缩短射程;当需要进行横向修正时,俯仰舵处于竖直位置起偏航作用,向左或向右打舵使弹向左或向右偏转。由于引信部分在修正过程中相对大地坐标系不转,在本文的实验中模型的舵偏角也呈固定状态。

本实验设计了2种模型,2种模型的外形结构尺寸相同,尖拱形头部、圆柱形模型身和船尾形模型尾;修正机构有一对俯仰舵和一对差动舵。同一种模型舵偏角度相同,不同种的模型舵偏角度不同,2种模型舵偏角度分别为4°和10°,对应的模型代号为H1和H2,模型外形简图如图2所示。模型外形尺寸满足亚跨音速的壅塞度和超音速下洞壁反射激波不打在模型上的条件[7]。

图2 组合体模型简图

实验过程中模型的俯仰舵(偏航舵)处于水平位置,舵朝上偏,零攻角下产生正升力;差动舵处于垂直位置。模型以尾支撑的方式安装在天平上,天平由风洞中的攻角机构支撑,图3为模型在风洞实验段照片。实验中攻角的变化范围为:-4°～+8°,马赫数范围为0.6～3.930 5。

图3 模型在风洞实验段

模型的参考面积选取最大横截面积S,俯仰力矩系数和压心系数的参考长度选总长度L、滚转力矩系数的参考长度选取最大截面对应的直径D,俯仰力矩系数参考点距模型头部顶点的相对距离(与模型长度之比)为0.646 7,滚转力矩系数参考轴取模型对称轴,压心系数参考点取弹顶点。实验模型单位长度的雷诺数见表1。

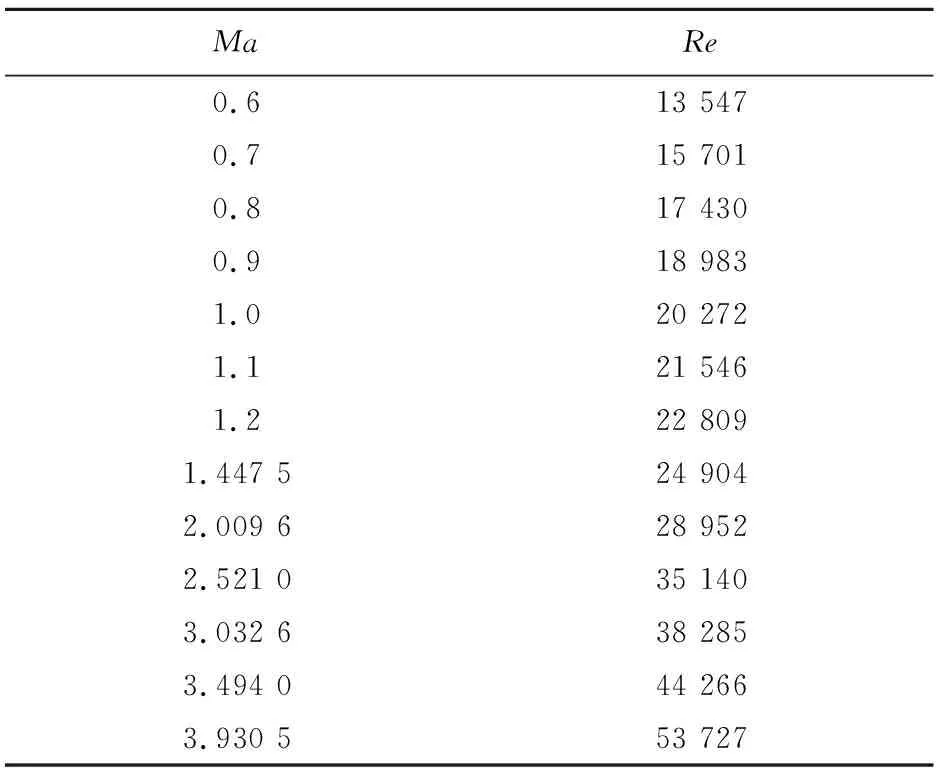
表1 实验模型单位长度雷诺数

2 实验结果及分析

2.1 阻力系数

图4给出了阻力系数CD随马赫数变化曲线,由图4分析发现,H1、H2模型阻力系数CD都是随马赫数先增大后减小的,在Ma=1.1时达到最大值。这是由于在跨音速附近弹身已产生激波,使得波阻迅速增大,而动压增加有限,所以阻力系数增加迅速。在超音速时,随着速度的继续增大,激波倾角越来越大,波阻有所降低,而动压增加明显,所以阻力系数呈下降趋势。该变化趋势符合气动规律。

图4 两模型阻力系数CD随Ma变化曲线

图4显示H2模型阻力系数大于H1模型,主要是舵偏角增加了迎风的面积,增加了阻力。亚音速时,随着速度的减小舵偏角增阻情况越明显,0°攻角时最大增阻率达到12.76%;跨超音速时,舵偏角增阻效果几乎相同,阻力系数曲线几乎平行,平均增阻率为4.82%。

图5为H1模型在马赫数Ma=2,攻角α=0°拍摄的纹影照片,从图中可以明显看到第1道激波出现在模型的头部,第2道激波出现在舵片前缘处,第3道激波出现在模型头部圆柱段与模型身部接触处。第1道激波与第2道激波有一定的交错,这是因为模型头部的尖锥半顶角没有舵片的前缘后掠角的余角大,波后气流有所减速,使得舵片前缘产生的激波倾角大于模型头部激波倾角,从而产生交错。第3道激波主要是由模型头部圆柱段与模型身部结合处有凹向台阶造成的,超音速气流受此扰动产生激波。

图5 H1模型Ma=2,α=0°时纹影照片

2.2 升力系数

在不同马赫数下,升力系数CL随攻角α的增加均呈线性增加,图6给出了Ma=2时升力系数随攻角变化曲线。由于模型的俯仰舵有一个正舵偏角,此舵偏角使舵片产生升力,所以模型处于0°攻角时总是有个正的升力系数。由于H2模型舵偏角大于H1模型,H2模型的升力系数在实验攻角范围内均大于H1模型的升力系数,所以图6中H2的升力系数曲线一直处于H1的上方。

图6 Ma=2时模型H1、H2的CL随α变化曲线

模型的差动舵面舵偏角在升力方向的投影面积较小,且产生的升力方向相反,对全弹的升力特性没有贡献。

图7所示为攻角α=8°时升力系数CL随Ma变化曲线。从图7中可见,升力系数CL随Ma变化趋势基本相同,在亚音速段升力系数先减小后增大,在马赫数Ma=0.8时达到最小值;在超音速阶段CL随Ma的增大而增大,在Ma=3.0附近达到最大值后随马赫数的增大而减小。同一Ma下,H2模型的CL均大于H1模型的CL,说明在实验范围内,舵偏角越大,模型的升力系数越大。

图7 H1、H2模型CL随Ma变化曲线

攻角α=0°时,升力系数CL随舵偏角δ变化曲线如图8所示。在舵偏角δ=0°,攻角α=0°时,由于模型的对称性,可以预知模型的升力系数CL=0 。由图8可以发现,升力系数CL随着舵偏角δ的增大而增大,仅在个别Ma下呈现线性特性,多数Ma下呈现非线性。

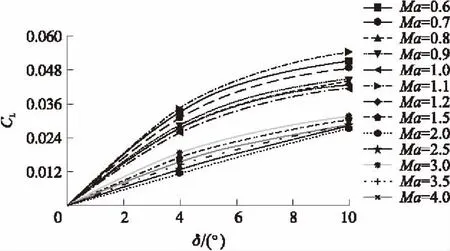
图8 α=0°时CL随δ变化曲线

2.3 俯仰力矩系数

图9给出了攻角α=4°时俯仰力矩系数Cm随Ma变化曲线,由图可见,两模型俯仰力矩系数的变化规律一致。在跨音速阶段Cm先波动上升再下降,在Ma=1.2时达到最小值;在超音速段,Ma>1.2后,Cm先上升并在Ma=1.5时达到最大值;Ma>1.5以后,Cm呈下降趋势。俯仰力矩是弹体法向力对参考点的力矩,它的大小取决于法向力的大小、合力作用点(压心)相对参考点的位置。模型法向力主要有3个来源:①模型体头部和靠近头部的圆柱产生的法向力;②模型体船尾部产生的法向力;③模型俯仰舵产生的法向力。在攻角为正时,模型头部、圆柱部和俯仰舵产生的法向力为正,且占主导地位,船尾部产生负法向力,其合力的作用点位于力矩参考点之前,所以产生正的俯仰力矩。

图9 α=4°时Cm随Ma变化曲线

在相同Ma、α情况下,模型头部、靠近头部的圆柱段及船尾部产生的法向力基本一致;不同的是俯仰舵产生的法向力,舵偏角越大则舵片上下面压差越大,产生的法向力越大;当俯仰力矩参考点位置相同时,H2模型的俯仰力矩系数Cm总是比H1模型的大。图10给出了Ma=2的俯仰力矩系数Cm随攻角α的变化曲线,结果显示俯仰力矩系数随攻角的增加呈线性增加,且H2模型的俯仰力矩曲线一直处于H1模型的上方。俯仰力矩系数大说明改变二维修正弹姿态的控制能力大,可以较容易地进行二维修正。

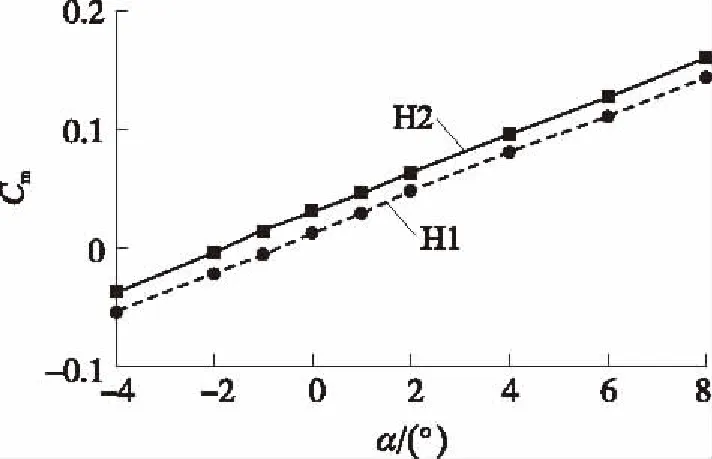
图10 Ma=2时Cm随α变化曲线

2.4 滚转力矩系数

图11给出了H1、H2模型的滚转力矩系数Cl随Ma的变化曲线。在跨音速阶段Cl曲线呈波动式下降趋势,在超音速阶段Cl随马赫数增加先增大后减小,在Ma=2附近达到最大值。滚转力矩主要是由处于模型头部上下位置的差动舵产生,由于一对舵偏角呈差动位置,一片舵片产生的垂直舵面的力与另一片舵面产生的垂直舵面的力方向相反,但对弹轴的力矩方向相同,其合力矩就是滚转力矩。随着差动舵偏角的增加,垂直舵面的力增加,滚转力矩也就增加,所以H2模型产生的滚转力矩大于H1模型产生的滚转力矩,滚转力矩系数大使得控制修正机构旋转的能力大。

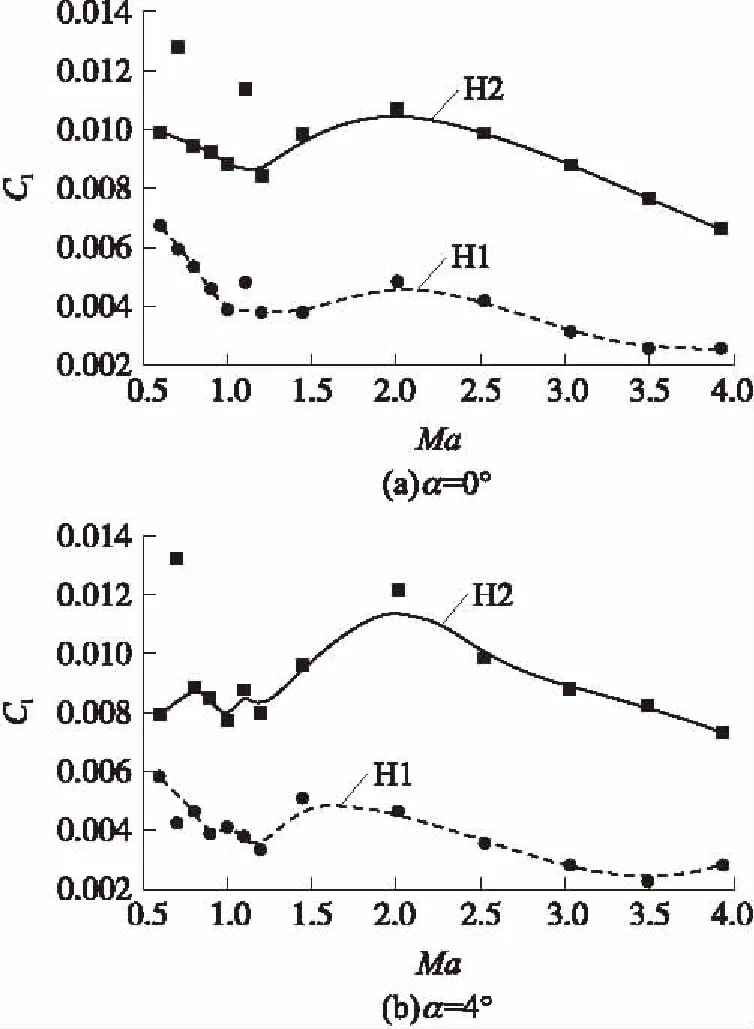
图11 不同攻角下Cl随Ma变化曲线

3 结论

旋转控制固定鸭舵二维弹道修正弹模型风洞实验研究表明:

①模型阻力系数随马赫数变化符合旋转弹阻力系数变化的气动规律,舵偏角的增加有一定的增阻效果,H2模型的阻力系数大于H1模型的阻力系数。亚音速下随着速度减小增阻效果增加,跨超音速下增阻效果几乎相同。

②在所研究的攻角范围内,升力系数随攻角增加呈线性增加,舵偏角的增加使得升力系数增加;0°攻角时,升力系数随舵偏角增加仅在个别马赫数下呈线性增加,多数马赫数下呈现非线性变化特性。

③俯仰力矩系数随攻角增加呈线性增加,随着舵偏角的增加而增加。在跨音速阶段,俯仰力矩系数先波动上升再下降,在Ma=1.2时达到最低值;Ma>1.2后先上升并在Ma=1.5时达到最大值;Ma>1.5以后呈下降趋势。

④滚转力矩系数随舵偏角的增大而增大;在亚跨音速下随马赫数增加而减小,Ma=1.1时达到最小值,当马赫数增加至2.0时达到最大值,以后随马赫数增加而减小。

[1] 张民权,刘东方,王冬梅,等.弹道修正弹发展综述[J].兵工学报,2010,31(12):127-130.

ZHANG Min-quan,LIU Dong-fang,WANG Dong-mei,et al.A summary for trajectory correction projectiles[J].Acta Armamentarii,2010,31(12):127-130.(in Chinese)

[2] 杨慧娟,霍鹏飞,黄峥.弹道修正弹修正执行机构综述[J].四川兵工学报,2011,32(1):7-9.

YANG Hui-juan,HUO Peng-fei,HUANG Zheng.Overview of correction executive mechanism on trajectory correction projectile[J].Journal of Sichuan Ordnance,2011,32(1):7-9.(in Chinese)

[3] 马宝华.战争、技术与引信——关于引信及引信技术的发展[J].探测与控制学报,2001,23(1):1-6.

MA Bao-hua.War,technology and fuze—about fuze and fuze technology development[J].Journal of Detection & Control,2001,23(1):1-6.(in Chinese)

[4] 华菊仙.弹道修正引信让笨弹变聪明[J].现代兵器,2006(8):13-16.

HUA Ju-xian.Trajectory correction fuze make bullet smarter[J].Modern Weaponry,2006(8):13-16.(in Chinese)

[5] 郝永平,孟庆宇,张嘉易.固定翼二维弹道修正弹气动特性分析[J].弹箭与制导学报,2012,32(3):171-173.

HAO Yong-ping,MENG Qing-yu,ZHANG Jia-yi.Aerodynamic characteristic ananlysison two-dimensional trajectory corrector shell with fixed-wing[J].Journal of Projectiles,Rockets,Missiles and Guidance,2012,32(3):171-173.(in Chinese)

[6] 张嘉易,王广,郝永平.二维弹道修正弹鸭舵修正机构气动特性研究[J].弹箭与制导学报,2013,33(2):121-124.

ZHANG Jia-yi,WANG Guang,HAO Yong-ping.The investigation of aerodynamic characteristics for two-dimensional trajectory correction projectile canard rudder device[J].Journal of Projectiles,Rockets,Missiles and Guidance,2013,33(2):121-124.(in Chinese)

[7] 王铁城.空气动力学实验技术[M].北京:国防工业出版社,1986.

WANG Tie-cheng.Aerodynamic experiment technology[M].Beijing:National Defence of Industry Press,1986.(in Chinese)