子母弹中心燃气式抛撒定容阶段试验及仿真
张博孜,王 浩,王珊珊
(南京理工大学 能源与动力工程学院,南京 210094)
子母弹抛撒技术按提供能量的来源可以分为惯性动能抛撒、机械分离抛撒和抛撒药燃气推动3种方式[1]。中心燃气式抛撒是抛撒药燃气推动方式的重要技术之一,该抛撒系统主要由传火管、燃气发生器、推弹装置(软性气囊或金属波纹管)和子弹组成,其内弹道过程可分为燃气发生器内部火药的燃烧阶段、火药燃气在推弹装置内的定容建压阶段和子弹起动到抛撒内弹道过程结束的变容做功3个阶段,抛撒过程示意如图1所示。这种抛撒技术具有子弹抛速可控、过载低的优势[1-4]。
在抛撒内弹道过程结束时,子弹既会获得相对于母弹的线速度,也可能获得翻转角速度。对不同的子母弹抛撒系统而言,有些角速度是必需的,有些角速度则是要尽量避免的。弹箍在抛撒系统中起约束子弹使其紧贴推弹装置的作用。研究表明,抛撒过程中子弹在弹箍断裂失效瞬间的受力状态是影响子弹抛撒速度和姿态的重要因素[5]。因此有必要对抛撒过程中定容阶段(弹箍断裂前)推弹装置内燃气流场进行深入研究,以便为子母弹的抛撒系统设计提供理论依据。

图1 中心燃气式抛撒过程示意图
本文设计了中心燃气式抛撒内弹道过程定容阶段的模拟实验,测试得到了模拟推弹装置内部流场的压力-时间曲线。建立了燃气发生器内部(包括传火管)的零维火药燃烧模型和推弹装置内定容流场的二维两相流模型;数值仿真结果与试验结果的对比验证了模型的可行性;针对燃气发生器小孔的分布和一类扰流机构对流场边界(推弹装置)受力的影响做了重点分析。
1 物理模型
1.1 试验装置简介
抛撒定容阶段试验装置由中心传火管、燃气发生器和定容钢桶组成,如图2所示。
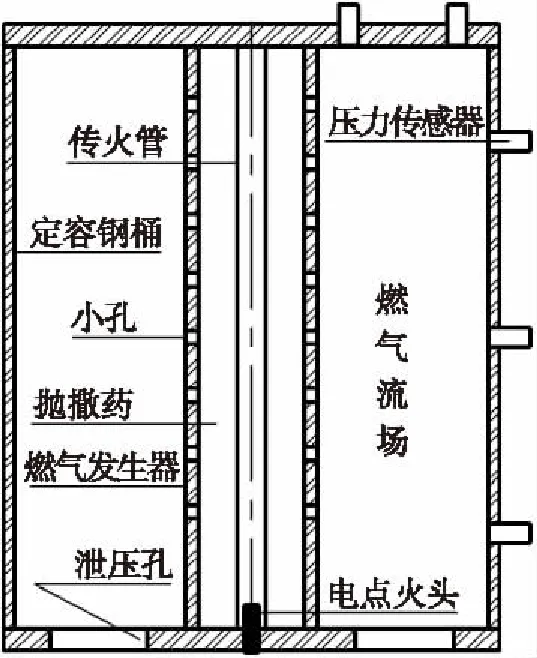
图2 抛撒定容阶段试验装置示意图
钢桶壁面和上端盖设有压力传感器,下端盖设有泄压孔和电点火头。钢桶容积与抛撒系统推弹装置的实际容积相同,泄压孔的破膜压力与使弹箍断裂的燃气压力相同。试验开始时,电点火头引燃传火管中的点火药,点火药燃气通过小孔流入燃气发生器并引燃抛撒药,燃气发生器内压力迅速升高至小孔破膜压力。小孔破膜后火药燃气和部分未燃完的火药颗粒由小孔流入定容钢桶内,钢桶内压力持续升高直至泄压孔破膜,试验结束。
1.2 主要假设
1.2.1 传火管和燃气发生器内零维模型假设
假设:
①只有点火药燃气流入燃气发生器,点火药燃气与抛撒药燃气瞬时混合,不考虑混合过程,混合燃气的质量、能量等于各单一火药燃气相应的质量、能量之和;
②点火药同时着火,抛撒药在传火管破膜后同时着火;
③点火药和抛撒药形状遵循几何燃烧定律,燃速遵循平均压力指数式;
④火药燃气服从“诺贝尔-阿贝尔”方程,火药力、余容、比热比等为常数,燃气发生器各喷孔的膜片同时破裂,燃气流动为等熵流动。
1.2.2 推弹装置内二维两相流模型假设
假设:
①流场为轴对称(轴向和径向)二维两相流;
②由火药颗粒群组成的固相连续分布在气相中,把火药颗粒群当作一种具有连续介质特性的拟流体来处理,且火药颗粒不可压缩;
③抛撒药燃气服从诺贝尔-阿贝尔状态方程;
④抛撒药颗粒服从几何燃烧定律和指数燃烧规律;
⑤假设相间阻力、热传导及化学反应等微观过程仅与两相当地平均状态相关;
⑥火药燃烧产物的组分保持不变,火药气体的热力学参数均为常量。
2 数学模型
2.1 传火管和燃气发生器内零维模型
1)火药燃烧规律。
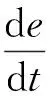
(4)
式中:σ,ψ分别为相对燃烧面积和相对已燃体积;Sp,mp分别为单颗火药瞬时表面积和质量;Sl,m1分别为单颗火药初始表面积和质量;χ,λ,μ为火药形状特征量;e,e1分别为当前和初始火药厚度的一半;μ1,n分别为燃速系数和燃速指数;p为燃气压力。
2)燃气状态方程。
式中:ρg,Tg分别为燃气密度和温度;β为燃气余容;Rg为火药燃气的气体常数。
3) 小孔流量公式[6]。
气相通过小孔的质量流量为
颗粒相通过小孔的质量流量为
式中:Skp为小孔的面积;co,g,co,p分别为气相流量系数和颗粒相流量系数;γ为绝热指数;p1表示燃气发生器内部压力;φ为气相空隙率;ρp,ρg分别为固相密度和气相密度;uin,g,r为由小孔喷出的火药燃气径向喷射速度分量。
2.2 推弹装置内两相流模型
式中:

(10)

除控制方程外,还需要相间阻力方程、相间传热方程、颗粒间应力等辅助方程,这些方程在两相流计算中应用较为成熟,详见文献[7]。
3 计算与试验结果
3.1 数值计算结果与试验结果对比
图3、图4分别给出了定容试验装置筒壁上靠近上、下端盖2处测试点的试验和计算的压力-时间对比曲线。可以看出,计算值与试验值基本吻合,这表明本文所建立的二维两相流模型能够较好地描述抛撒内弹道过程定容阶段的两相内流场的变化规律。压力曲线呈波动性上升,说明在试验装置内部沿轴向存在明显的压力波。泄压孔破膜压力取3 MPa,由于泄压孔集中于下端盖,因此出现了在3.5 ms后上、下端压力曲线分离的现象,靠近泄压孔一侧压力明显低于另一侧。
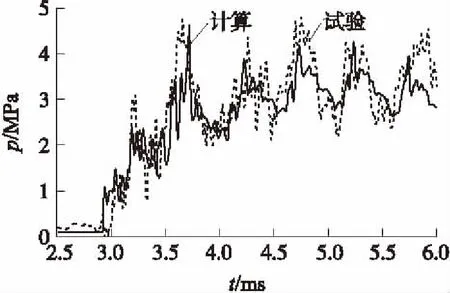
图3 筒壁靠近上端盖处p-t曲线
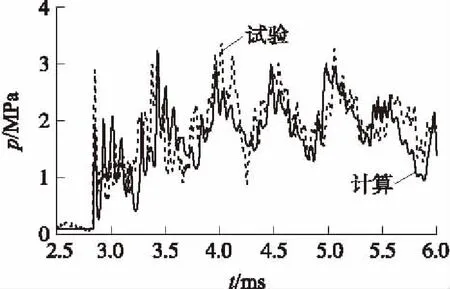
图4 筒壁靠近下端盖处p-t曲线
3.2 边界受力分析
定容试验装置的筒壁主要用来模拟抛撒内弹道过程中的推弹装置。推弹装置在弹箍断裂、弹丸起动瞬间的受力状态直接影响子弹的抛撒速度和姿态,受力状态的主要指标体现为推弹装置所受合力与合力矩大小(方向取顺时针为正)。子母弹抛撒系统的研制中,常通过改变燃气发生器小孔的分布或在抛撒装置内添加扰流机构改变流场的流动状态,进而改变流场边界的受力状态。下文主要分析这2项可变结构参数对边界受力的影响。
3.2.1 燃气发生器小孔分布对边界受力的影响
图5、图6分别为燃气发生器小孔均布和小孔向一侧偏置情况下边界所受合力F和合力矩M随时间变化的对比曲线,其中小孔总面积保持不变。图5中2条对比曲线几乎重合,表明改变小孔分布状态对边界所受合力大小影响有限。从图6看出,在小孔均匀分布状态下边界所受合力矩仅在0附近有微小波动;而当小孔分布向上偏置,在燃气射流首次到达边界时出现合力矩的正向激变,但随后迅速回归并在0附近呈振幅逐渐衰减的周期性震荡。

图5 不同小孔分布时边界F-t曲线

图6 不同小孔分布时边界M-t曲线
虽然利用燃气发生器小孔的偏置能使子弹受到较大的合力矩,进而使子弹起动瞬间获得较高的翻转角加速度,但合力矩的方向和大小随时间发生变化,且变化周期很短。如果弹箍断裂的时机稍有偏差,就可能造成与设计初衷相悖的结果。
3.2.2 扰流机构对边界受力的影响
通过在推弹装置内部安装扰流板的方式也能达到改变流场特性的目的。本文对比计算了小孔偏置且扰流板同向偏置和小孔偏置但扰流板反向偏置2种不同结构的定容燃气流场,2种结构示意图如图7所示。图8和图9分别为2种结构下边界所受合力与合力矩大小的时间历程曲线。图8显示,虽然扰流板位置不同,但边界所受合力基本相同;结合图5可以看出,有扰流板情况下边界所受合力略大于无扰流板情况,因为扰流装置约占用流场7%的体积,导致内部压力偏高。虽然2种扰流板位置上下对称,但由于燃气发生器小孔分布偏置,因此2种状态下边界所受合力矩-时间曲线并不对称,见图9。当扰流板与小孔同向偏置时,边界所受合力矩在经过第1个负向峰值后出现正向的平台期。而当扰流板与小孔反向偏置时,合力矩经第一个正向峰值后迅速趋于0附近震荡。“孔偏上、板偏下”与“孔偏上、无板”2种工况的边界合力矩相比,如图9和图6,前者第1次正向峰值高于后者60%,第1次负向峰值则低于后者50%。

图7 不同扰流机构示意图

图8 不同扰流结构时边界F-t曲线

图9 不同扰流结构时边界M-t曲线
与单纯靠小孔偏置形成的周期性力矩相比,加装扰流板形成的力矩平台期持续时间较长,通过合理设计弹箍断裂时机,能保证子弹在起动瞬间受到稳定的翻转力矩,从而达到控制子弹抛撒姿态的目的。
4 结论
①本文建立的数理模型能够较好地描述子母弹中心燃气式抛撒内弹道定容阶段燃气流场的变化规律,可以为子母弹抛撒系统的设计提供理论方法。
②计算表明,仅改变燃气发生器小孔分布对推弹装置受力影响微小,但所受合力矩呈振幅逐渐衰减的周期性震荡。由于震荡周期较短(1 ms左右),因此在设计抛撒系统时很难把握子弹的起动时机,这会给子弹的抛撒姿态带来较大的不确定性,对于抛撒的稳定性不利。
③添加扰流板改变流场结构并结合燃气发生器小孔的偏置,能使推弹装置所受合力矩在流场建压后形成一段平台期。平台期的持续时间相比震荡周期明显增长,这为设计子弹的起动时机、保证子弹的抛撒姿态提供了理论依据。此外,扰流机构的形式并不局限于此,通过数值计算方式探索不同类型、不同大小和位置的扰流机构对抛撒性能的影响,在提高子母弹抛撒有效性方面具有重要意义。
[1] 张本,陆军.子母弹抛撒技术综述[J].四川兵工学报,2006,27(3):26-29.
ZHANG Ben,LU Jun.Overview of shrapnel casting technique[J].Sichuan Ordnance Journal,2006,27(3):26-29.(in Chinese)
[2] 王浩,黄明,邵志坚.子母弹燃气囊抛撒模型及其计算[J].弹道学报,2000,12(3):11-16.
WANG Hao,HUANG Ming,SHAO Zhi-jian.A model of the firing process of combustion gasbag of submunition and its simulation[J].Journal of Ballistics,2000,12(3):11-16.(in Chinese)
[3] 孟会林,孙新利,姬国勋.子母弹抛撒过程数值模拟及其试验[J].弹箭与制导学报,2004,24(4):317-321.
MENG Hui-lin,SUN Xin-li,JI Guo-xun.Test and numerical simulation of the bullets spreading process of a primary-secondary bomb[J].Journal of Projectiles,Rockets,Missiles and Guidance,2004,24(4):317-321.(in Chinese)
[4] 冯顺山,王刚.子母弹金属囊式抛撒计算机仿真[J].计算机仿真,2012,29(10):59-62.
FENG Shun-shan,WANG Gang.Compusimu of cluser warhead metal capsule dispersing[J].Computer Simulation,2012,29(10):59-62.(in Chinese)
[5] 王刚,冯顺山.爆炸抛撒子弹翻转运动研究[J].中北大学学报,2008,29(3):210-213.
WANG Gang,FENG Shun-shan.Study on submunition’s turnover movement in explosion dispersion[J].Journal of North University of China,2008,29(3):210-213.(in Chinese)
[6] 金志明.枪炮内弹道学[M].北京:北京理工大学出版社,2004.
JIN Zhi-ming.Gun interior ballistics[M].Beijing:Beijing Institute of Technology Press,2004.(in Chinese)
[7] 翁春生,王浩.计算内弹道学[M].北京:国防工业出版社,2006:1-200.
WENG Chun-sheng,WANG Hao.Computational interior ballistics[M].Beijing:National Defence Industry Press,2006.(in Chinese)

