弹头形状对高速侵彻效应的影响

宋梅利,王晓鸣,李文彬,刘志林

(南京理工大学 智能弹药技术国防重点学科实验室,南京 210094)

研究弹体对混凝土类硬目标的高速侵彻效应对战斗部研制和防护结构设计都极具意义。影响弹体侵彻能力的因素很多,如弹体着靶速度、弹头形状、弹体长径比、弹体质量、靶体强度、弹体运动条件等,其中,弹头形状的影响是重要方面之一。目前,国内外学者对小口径卵型、锥型弹体(口径小于30 mm)高速侵彻时的弹体阻力模型、弹头质量侵蚀模型、侵彻深度模型、侵彻深度影响因素等方面开展了许多工作。陈小伟[1]等根据刚性弹侵彻动力学的量纲-侵彻深度公式,分析了刚性弹侵彻过程中弹丸所受的靶板阻力,针对不同弹头形状(尖卵型、半球型、平头型、尖锥型),理论分析了相应的撞击速度阈值,该结果可以较准确地预测侵彻深度。何丽灵[2]等研究了弹头形状变化对侵彻能力的影响,提出了弹头形状演化的迭代计算模型,该迭代算法用于锥型弹时,发现锥角越大,弹头钝化趋势越弱。石志勇[3]等在轻气炮上进行了3种弹头形状的小尺寸模型弹侵彻水泥砂浆靶试验,结果表明,弹头形状对侵彻深度有较大的影响,在相同撞击速度下,半锥角α=22.5°的锥型长杆弹的侵彻深度比α=45°的锥型弹的侵彻深度要深,卵型弹体的弹头曲率比CRH(caliber radius head)值越大,侵深越大。皮爱国等[4]对卵型弹头部形状进行优化以减少弹头所受阻力,提高弹体侵彻能力。康海峰等[5]通过理论计算和数值模拟得到了柱形弹体和不同半锥角的锥型弹体的弹道偏移量和垂直侵深的变化规律。范少博等[6]数值模拟研究了卵型弹头在侵彻效能、抗侵蚀能力及装药安定性上都优于锥型弹头。国内外研究者从理论、试验和数值仿真三方面对不同弹头的弹体侵彻混凝土靶进行了很多研究工作,但着靶速度范围大多在1 200 m/s以下,且对双弧线型弹体的侵彻研究也少见报道。为了研究60 mm口径不同弹头形状的弹体在高速(800～1 400 m/s)侵彻下的侵彻效应,本文从试验和理论两方面对尖卵型和双弧线型弹体的侵彻能力进行了研究,所得结论对高速攻击混凝土类目标的弹体设计有一定的指导意义。

本文用60 mm口径的弹体对半无限厚素混凝土靶进行了高速侵彻试验,弹头形状分别为尖卵型(CRH为3)和双弧线型,弹体撞击速度在800～1 400 m/s之间,得到了不同速度下侵彻深度、弹坑深度、弹体响应等参数。建立了尖卵型和双弧线型弹头部形状函数,在试验结果和空腔膨胀理论的基础上,分析了2种不同弹头形状弹体在高速正侵彻过程中的受力情况,建立了弹体阻力模型,根据牛顿定律,得到弹体的运动方程,编程求解了弹体的侵彻深度。

1 试验方案与结果

1.1 试验方案

试验弹体为60 mm口径,弹长为300 mm,长径比为5,侵彻战斗部质量约为4 kg,弹壳材料用30CrMnSiNi2A,并经过淬火和回火热处理,热处理后测得材料硬度HRC为48～52,抗拉强度为1 650 MPa。图1为弹体和弹托实物。素混凝土圆柱靶体直径为1.8 m(弹径的30倍),厚度分别为2 m和3 m,靶体按照C40配合比设计,实测标准抗压强度为47.6 MPa。靶体边界用8 mm厚的钢板箍紧。

图1 试验前弹体和弹托实物

试验现场布置如图2所示。发射装置用105 mm滑膛炮,通过改变装药量调整弹速在800～1 400 m/s之间。本次试验为正侵彻,为减少弹体着靶时的着角和攻角,炮口尽量靠近靶体(8 m),同时用张开式尾翼弹体保证弹体出炮口后的飞行稳定性。用金属网靶和测试仪测量弹速,在靶前放置45°的镜子配合高速录像拍摄弹体着靶前姿态及着靶速度。

图2 试验现场布置图

1.2 试验结果

对以上2种弹型共进行了9发正侵彻试验,侵彻前后弹体的参数见表1。表中,v0为弹体着靶速度,m0为试验前侵彻体质量,m为试验后侵彻体质量,L0为试验前侵彻体长度,L为试验后弹体的剩余长度,Δm/m0为质量损失百分比,ΔL/L0为长度损失百分比。从表1可以看出,对口径为60 mm的尖卵型和双弧线型弹体,当弹体以800～1 400 m/s的速度侵彻混凝土靶时,所有弹体的长度损失都小于5%,质量侵蚀低于5%,因此可近似认为刚性弹侵彻。

表1 试验前后弹体的参数表

弹体的运动条件及靶的破坏情况见表2。表中,αv为铅垂面弹体着角,αh为水平面弹体着角,βv为铅垂面攻角,βh为水平面攻角,H为侵彻深度,Hk为成坑深度,Dk为成坑直径。由表2弹体着靶条件看出,弹体飞行较稳定。对尖卵型弹头,随着速度的增大,水平和铅垂平面弹体的着角和攻角都小于2°,双弧线型弹头飞行稳定性较尖卵形弹头差,但着角和攻角均小于5°,因此可近似认为弹体垂直于承弹面着靶。

回收到的9发试验弹体均无明显的变形,部分回收弹见图3。由于回收弹体外表面粘有混凝土碎渣,且有的弹体侵彻过程中底部碎掉,故部分弹体无法获得侵彻后剩余质量。

表2 弹体的运动条件及靶的破坏情况

图3 部分回收弹体

侵彻深度随弹体着靶速度变化曲线见图4。

图4 侵彻深度随弹体着靶速度的变化

表2和图4显示,对尖卵型弹体,随着着靶速度的增大,侵彻深度随速度呈线性增加的趋势,这一现象与Forrestal M J[7]、Nelson[8]等学者的研究结果相悖。文献[7]中当弹体速度超过1 200 m/s后,弹体侵蚀严重,这导致侵深随着速度的增大而减少,主要原因是文献[7-8]研究的弹体直径较小(<30.5 mm),弹体材料为4340钢,热处理后弹体硬度HRC为38～40,当着靶速度超过1 200 m/s时,过大的撞击压力使弹体材料发生热软化,弹体强度下降导致结构破坏,从而侵彻能力下降。而本文研究的弹体材料为高强度的合金钢,热处理后可获得较高的强度和硬度,当弹体速度增加到1 400 m/s时,弹体材料的应变率受冲击压力的影响较少,弹体结构保持较好,质量侵蚀小于5%,故侵彻机理近似刚性弹侵彻。侵彻试验后,混凝土靶体着弹面形成了漏斗形弹坑,靶体着弹面有数十条对称分布的径向裂纹,尖卵型弹头侵彻后的弹坑平均直径及坑深随速度的变化曲线见图5。当弹体速度从833 m/s增大到1 401.8 m/s时,弹坑直径增大128%,弹坑深度增加约58%。图6为弹体着速为1 242 m/s和1 315 m/s时混凝土靶着弹面的开坑形状,试验中发现,当弹体速度超过1 100 m/s后,虽然靶表面的径向裂纹增多,但漏斗坑直径和坑深随速度的增大增加不明显。

图5 漏斗坑平均直径和坑深随着靶速度的变化

图6 混凝土靶着弹面的开坑形状

2 尖卵型和双弧线型弹体侵彻深度的理论模型计算

计算弹体侵彻混凝土靶的侵彻公式很多,每种经验公式都有各自的应用范围和适用条件,而真正应用较广且精度较高的公式并不多,特别是高速侵彻时弹体的侵彻深度计算更为复杂。本文研究的弹体和靶体相关参数如试验方案所述,根据实验结果,在所研究的速度范围内弹体可近似认为刚性侵彻。

根据考虑混凝土空隙压实效应的球形空腔膨胀理论,材料的屈服准则采用Mohr-Coulumb准则,得到空腔膨胀压力σr与膨胀速度v′之间的关系[9]:

由式(1)可以得到弹体高速侵彻混凝土靶时弹体头部表面受到的靶体对其轴向阻力F与弹体侵彻速度v之间的关系,根据牛顿第二运动定律知:

(2)

式中:a0,a1,a2为常数;l为弹丸头部侵入靶体的长度;φ(x)为弹头部形状函数;φx(x)为φ(x)对x的导数;r为弹丸的半径;v为弹体侵彻过程中的瞬时速度;c为开坑段阻力系数。

开坑阶段,根据Forrestal的研究[9],假定弹体受到混凝土的阻力为

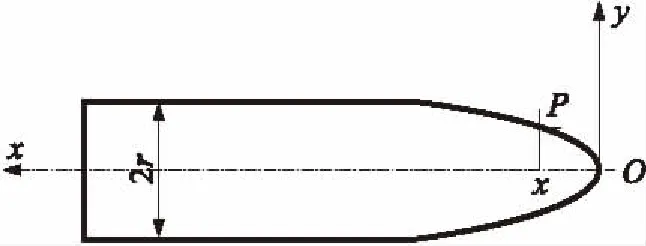
F=cz0

(3)

代入初始条件z(t=0)=0和v(t=0)=v0,上述方程可以解得:

ω2=c/m

(8)

式中:ω为一个引入常数。假定t1时弹体结束开坑阶段,v1为弹体此时的速度,由于侵彻过程中弹体的速度和所受阻力的连续性,可以得到t1时刻有:

-mωv0sinωt1=F(v1)

(9)

v0cosωt1=v1

(10)

(11)

求解方程(9)～方程(11)得v1和c:

整个侵彻过程的弹丸阻力与弹丸速度关系已知,将整个侵彻过程分成N个时间步长为dt的微小运动过程,在dt内有:

对于尖卵型弹丸,建立如图7所示坐标系,弹头部任一点P的函数表达式为

式中:φ为弹头曲率比(CRH),φ=s/(2r),s为弹头母线曲率半径。

图7 尖卵型弹头部

双弧线型弹丸头部由2段不同曲率半径的圆弧用中间相切的圆弧线连接而成,结构如图8所示。

图8 双弧线型弹头结构

计算弹丸头部侵彻阻力时,将其分为3段,分别计算每段所受混凝土的侵彻阻力。第1段圆弧的曲率半径为R1,所受阻力F1可看成弹丸半径为r、曲率比φ1=R1/(2r)的尖卵型弹丸进行计算;第3段圆弧曲率半径为R3,与第1段圆弧阻力计算类似,可将其看成弹丸半径为r1,曲率比φ3=R3/(2r1)的尖卵形弹丸进行计算。第2段圆弧类似翻转后的卵形曲线,曲率半径为R2,其所受的侵彻阻力可按弹丸半径为r2-r1,曲率比φ2=R2/(2r2-2r1)的尖卵型弹丸进行计算。根据上述的几何关系,双弧线型弹体的头部形状函数表达式为

φ(x)=

(15)

将式(14)、式(15)分别代入式(2)和式(13)进行数值迭代计算,即可得到尖卵型和双弧线型弹体以不同速度侵彻混凝土的侵彻深度。表3为尖卵型弹体侵彻混凝土时理论计算侵深和试验测量侵深的比较。表4为双弧线型弹体侵彻混凝土时理论计算侵深和试验测量侵深的比较。表3和表4中,HE为试验测得侵深,HT为理论计算侵深,Δ为试验与理论侵深差值百分比。

表3 尖卵型弹体侵彻混凝土时理论计算侵深和试验测量侵深的比较

表4 双弧线型弹体侵彻混凝土时理论计算侵深和试验测量侵深的比较

表3显示,尖卵型弹体理论计算侵深与试验测量侵深误差均在10%以内,说明本文所用的理论计算方法是可行的,该方法适用于60 mm口径的卵型头部弹体以800～1 400 m/s的速度侵彻素混凝土时的侵彻深度计算。表4中受试验条件的限制,双弧线型弹体进行了3发高速侵彻试验。本文所用理论计算侵深与试验侵深误差小于10%,故理论计算结果是可信的。表3和表4还显示理论计算侵彻深度比试验测量值都略大,主要原因是本文理论模型计算侵深时假设弹体是刚性弹,忽略了弹丸质量损失和弹丸头部形状变化。而表1显示试验后弹体的长度损失虽然小于5%,但都不为0。图9是弹体质量、着靶速度及靶体一致的条件下,尖卵型和双弧线型弹体侵彻深度理论计算值的比较,可以看出,相同条件时双弧线型弹体的侵彻能力较尖卵型弹体高约9%。

图9 尖卵型和双弧线型弹体侵彻深度理论值比较

3 结论

根据上述对60 mm口径弹体开展的高速侵彻试验及2种弹头形状的侵彻深度理论模型分析,可得出以下结论:

①60 mm口径弹体高速侵彻素混凝土靶试验结果表明,对于材料为30CrMnSiNi2A,热处理后抗拉强度约为1 650 MPa的弹体,以800～1 400 m/s的速度侵彻C40的素混凝土靶时,弹体质量侵蚀和长度缩短均小于5%,弹体可近似认为刚性侵彻;

②建立了尖卵型和双弧线型弹体的头部形状函数,在空腔膨胀理论的基础上,分析了2种不同弹头形状弹体在高速正侵彻过程中的受力情况,建立了弹体阻力模型,得到弹体的运动方程,用数值迭代法求解了弹体的侵彻深度,理论计算值与试验测量结果误差小于10%。

③尖卵型和双弧线型弹体侵彻深度理论模型计算结果显示,弹体质量、着靶速度及靶体一致的条件下,双弧线型弹体的侵彻能力较尖卵型弹体高约9%。

[1] 陈小伟,李继承.刚性弹侵彻深度和阻力的比较分析[J].爆炸与冲击,2009,29(6):584-589.

CHEN Xiao-wei,LI Ji-cheng.Analysis of penetration depthand resistive force in the deep penetration of a rigid projectile[J].Explosion and Shock Waves,2009,29(6):584-589.(in Chinese)

[2] 何丽灵,陈小伟.弹体形状演化模拟的应用[J].固体力学学报,2010,31(专辑):103-108.

HE Li-ling,CHEN Xiao-wei.Application of direct simulation of viriation of projectile nose[J].Chinese Journal of Solid Mechanics,2010,31(Album):103-108.(in Chinese)

[3] 石志勇,汤文辉,赵国民,等.长杆射弹对钢纤维混凝土靶开坑特性的实验研究[J].国防科技大学学报,2004,26(5):26-29.

SHI Zhi-yong,TANG Wen-hui,ZHAO Guo-min,et al.Experimental study of the crater performance about the long rod projectile penetrating steel fiber reinforced concrete target[J].Journal of National University of Defense Technology,2004,26(5):26-29.(in Chinese)

[4] 皮爱国,黄风雷.基于变分法原理的侵彻弹体头部形状优化设计[J].弹箭与制导学报,2007,27(4):126-130.

PI Ai-guo,HUANG Feng-lei.A method based on variation theory for the shape optimization of penetrator nose shape[J].Journal of Projectiles,Rockets,Missiles and Guidance,2007,27(4):126-130.(in Chinese)

[5] 康海峰,代廷静,沈培辉.弹体形状对侵彻弹道的影响分析[J].弹箭与制导学报,2012,32(2):73-76.

KANG Hai-feng,DAI Ting-jing,SHEN Pei-hui.The analysis of the influence of projectiles shape on penetration trajectory[J].Journal of Projectiles,Rockets,Missiles and Guidance,2012,32(2):73-76.(in Chinese)

[6] 范少博,陈智刚,郭光全.动能侵彻体头部形状对其侵彻效能影响研究[C]//第七届全国爆炸力学实验技术学会会议论文集.杭州:中国力学学会爆炸力学专业委员会,2012:12-13.

FAN Shao-bo,CHEN Zhi-gang,GUO Guang-quan.Kinetic energy penetrator head shape of the performance impact of its penetration[C]//The 7th National Institute of Experimental Techniques Explosion Conference Proceedings.Hangzhou:Professional Committee of Explosion,Chinese Society of Theoretical and Applied Mechanics,2012:12-13.(in Chinese)

[7] FORRESTAL M J,FREW D J,HANCHAK S J,et al.Penetration of grout and concrete targets with ogive-nose steel projectiles[J].International Journal of Impact Engineering,1996,18(5):465-476.

[8] NELSON R W.Low-yield earth-penetrating nuclear weapons[J].Science and Global Security,2002(10):1-20.

[9] FORRESTAL M J,TZOU D Y.A spherical cavity expansion penetration model for concrete targets[J].International Journal of Solids and Structures,1997,34:4 127-4 146.