速射火炮立靶密集度序列建模

朱 凯,王 军,薄煜明

(南京理工大学 自动化学院,南京 210094)

武器系统的立靶密集度是系统精度的重要组成部分,它分为弹道炮的立靶密集度和战斗炮的立靶密集度。前者是指固定火炮身管时射弹的立靶密集度,造成射弹散布的主要原因是单发炮弹的个体差异;后者是指不固定火炮身管时射弹的立靶密集度,造成射弹散布的主要原因除了单发炮弹的个体差异外,还包括射击冲击载荷的影响。对于战斗炮的立靶密集度,传统的射击效力分析方法中并未考虑射击冲击载荷的影响,即认为射弹散布为不相关的平稳正态序列。

随着武器系统射速的提高,武器身管冲击载荷所带来的弱相关误差对立靶密集度的影响已经不能被忽略。为了准确分析速射火炮立靶密集度,需要记录带弹序的立靶密集度序列。早期的木板靶法精度很低,且射弹数较多时读数不准确;声学靶法可以提高立靶密集度的测量精度[1],但当火炮射速很高时会漏测;照相测量法可以克服木板法与声学靶法的缺陷,并能进行密集度测量与弹序识别[2];随着光电技术的发展,光电靶能更准确地记录高射速火炮立靶密集度试验的弹序与数据,文献[3]提出了一种带弹序的高射速火炮立靶密集度测试技术,实现了弹丸的排序测试。在火炮立靶密集度分析中,文献[4]用实际射击结果证明了连发武器的射弹散布与火炮冲击载荷有很大关系;文献[5]建立了战斗炮立靶密集度的状态方程,并对实测脱靶量数据进行了分析,计算了一阶相关系数,并给出了相关系数的检测方法。但对于高射速火炮而言,一阶模型对其立靶密集度的描述具有一定的误差。本文将时间序列建模理论运用到高炮武器系统的射击效力分析领域,对速射火炮的立靶密集度序列建立了数学模型;模型残差比较以及模型验证证明了本文模型比一阶误差模型具有更高的精度。

1 时间序列建模

1.1 基础理论

作为概率统计学中的一个重要分支,时间序列分析运用概率统计的方法分析和处理随时间变化的随机数据序列,包括模型建立、参数估计以及预测和控制等内容。若一个时间序列{yt},t=1,2,…,N,是平稳、0均值的,则它一定能用如下差分方程描述[6]:

yt-φ1yt-1-φ2yt-2-…-φpyt-p=
at-θ1at-1-θ2at-2-…-θqat-q

(1)

式中:yt为时间序列{yt}在t时刻的值;φi(i=1,2,…,p)与θj(j=1,2,…,q)分别表示序列的自回归参数与滑动平均参数;序列{at}则称为残差序列。若式(1)能准确地描述该时间序列,则序列{at}为白噪声。当φi全为0而θj不全为0时,称式(1)为q阶滑动平均模型MA(q);当θj全为0而φi不全为0时,称式(1)为p阶自回归模型AR(p);若φi,θj都不全为0,此时式(1)称为p阶自回归q阶滑动平均模型,记为ARMA (p,q)模型。

1.2 时间序列的研究工具

在对时间序列进行建模之前,需要分析其性质,以判断其是否可以建立ARMA模型。自相关和偏自相关则是重要的研究工具。

1)自相关。

构成时间序列的每个值yt,yt-1,…,yt-k之间存在一定的相关关系,其由自相关系数rk度量,但它并不是单纯的相关关系。例如测量值yt与yt-k之间存在yt-1,yt-2,…,yt-k+1这k-1个中间变量,它们会影响到这两者之间的相关性,将其纳入考虑范围时即为自相关。yt与yt-k之间的自相关系数表示为

(2)

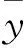
2)偏自相关。

如果需要把中间变量的影响因素剔除,则引入偏自相关的概念。对于时间序列yt中的2个值yt与yt-k,在给定yt-1,yt-2,…,yt-k+1这k-1个中间变量的条件下,yt与yt-k之间的条件相关关系即为偏自相关,即在不考虑中间变量的前提下,其相关程度用偏自相关系数φk,k来表示:

(3)

式中:rk是滞后k个间隔的自相关系数,且

φk,m=φk-1,m-φk,kφk-1,k-mm=1,2,…,k-1

(4)

在对时间序列进行分析时,要综合考虑序列的自相关与偏自相关,以保证分析的准确性。

1.3 平稳性检验

检验时间序列的平稳性通常有2种方法,即图检验法和单位根检验法。

1)图检验法。

对于一个平稳时间序列,其均值应始终为常数。如果时间序列的所有数据的取值始终在一个常值附近随机变化,且变化范围有界,则这个时间序列大致上可被认为是平稳的;反之,如果数据有明显的趋势性或周期性,则大致上可判断时间序列是非平稳的。图检验法只能做大致判断,是一种经验方法,而不是一种严谨的数学方法。

2)单位根检验法。

在时间序列的平稳性检验中,通常使用单位根检验法。即对于一个时间序列,通过判定其自回归特征方程的特征根是否都在单位圆内,来检验时间序列是否平稳。在单位根检验中,常用的是迪基-福勒(DF)检验与增广的迪基-福勒(ADF)检验。DF检验只适用于一阶自回归过程的平稳性检验,p阶自回归过程的平稳性则需要ADF检验[7]。单位根检验的具体步骤见文献[8]。

2 立靶密集度序列建模

实测得一组53发的战斗炮的立靶密集度方位落点X数据,如表1所示。为了将本文模型与一阶模型进行比较,这里取前45个点数据用于建模,后8个点用于做一阶模型与本文模型的预测值和测量值的比较。表中,N为发射弹数。

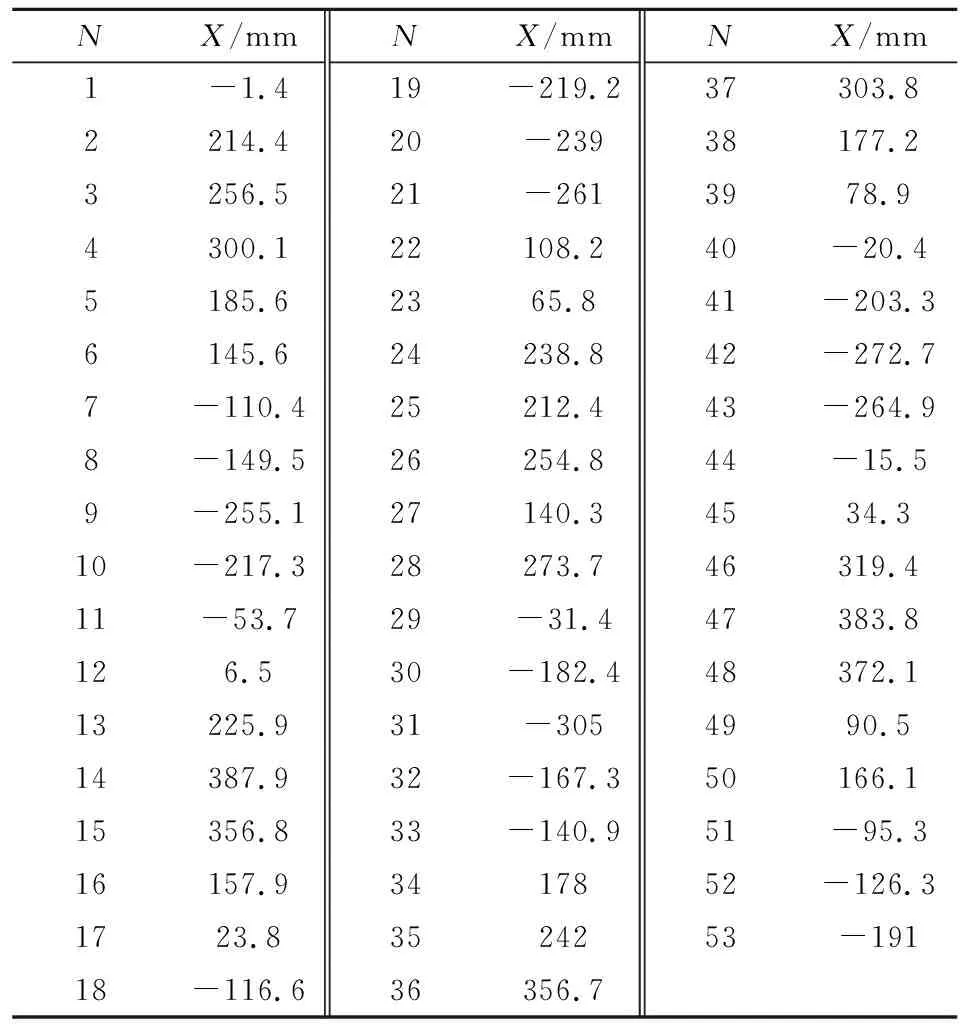
表1 实测脱靶量方位数据

2.1 平稳性分析

将前45个数据去除系统误差,得到0均值的序列,其时间序列图如图1所示。

图1 立靶密集度时序图

从时序图可以看出,脱靶量数据在0均值附近波动,初步判定为平稳。利用单位根检验法对其进行平稳性检验,EVIEWS检验t统计量的值小于各个显著性水平下的临界值,所以拒绝原假设,认为立靶密集度序列不存在单位根,故立靶密集度序列是平稳的。

2.2 模型的确定

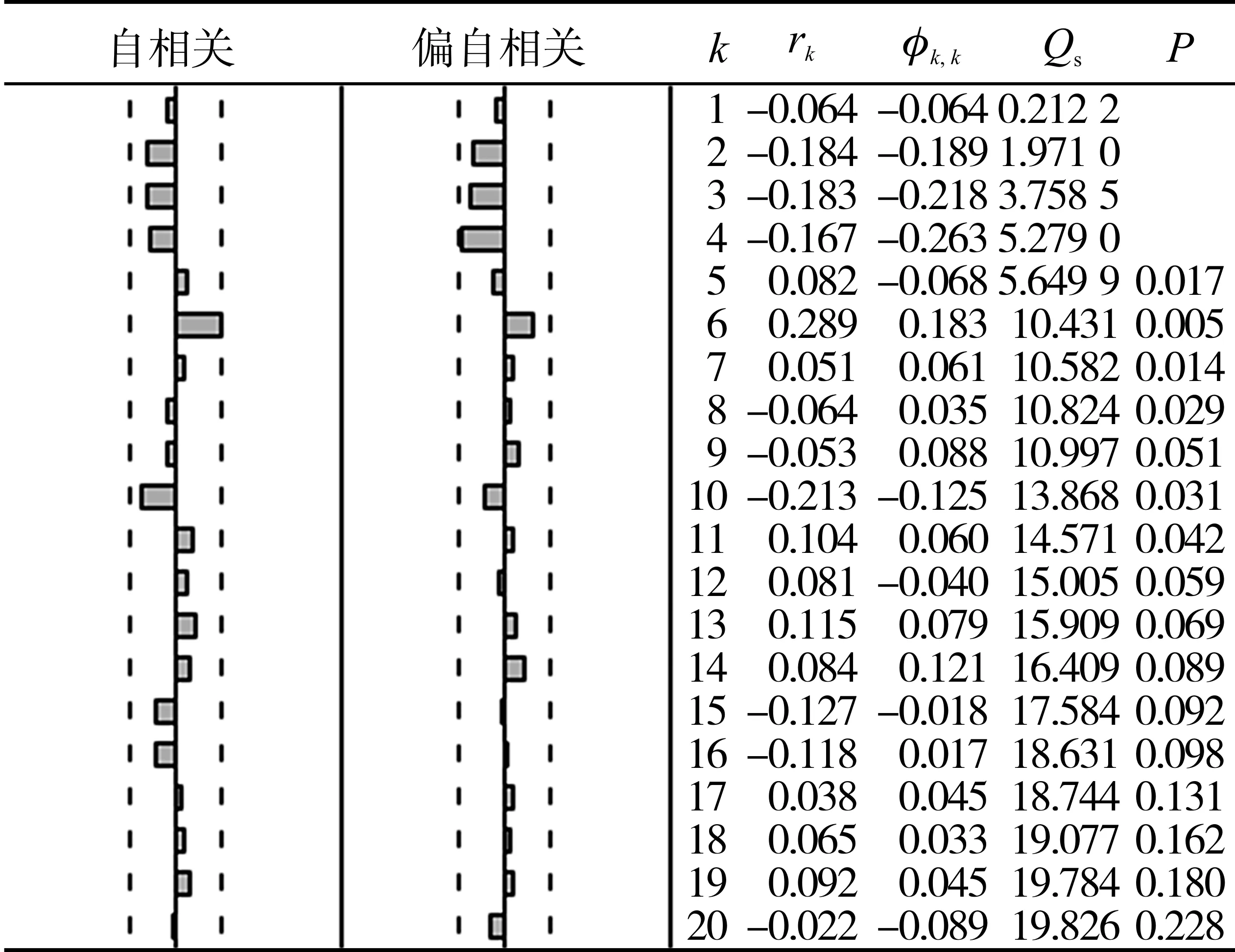
使用EVIEWS软件对立靶密集度序列的自相关和偏相关进行分析,结果如表2所示。表中,左半部分为序列的自相关与偏自相关分析图,右半部分包含5列数据,其中,k为滞后期,rk为自相关系数,φk,k为偏自相关系数,Qs为Q统计量,P为相伴概率。

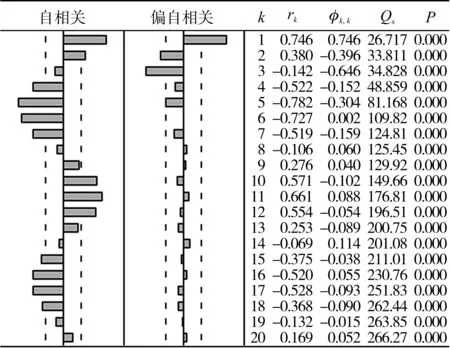
表2 立靶密集度的自相关与偏自相关

由自相关函数易知立靶密集度数据序列具有明显的相关性,即传统射击效力中平稳不相关的假定不再适用,冲击载荷带来的弱相关误差必须纳入考虑范围。

1)一阶模型。

在传统的射击效力分析方法中,0均值弱相关序列yt为一阶平稳弱相关,有

式中:r为一阶相关系数,wt为白噪声。

yt+1=ryt+at

(6)

即AR(1)模型。

对非0均值的原序列,EVIEWS一阶建模结果为

2)高阶模型。

根据样本自相关与偏自相关的拖尾性与截尾性选择适当的模型进行建模[9],定阶的原则如表3所示。

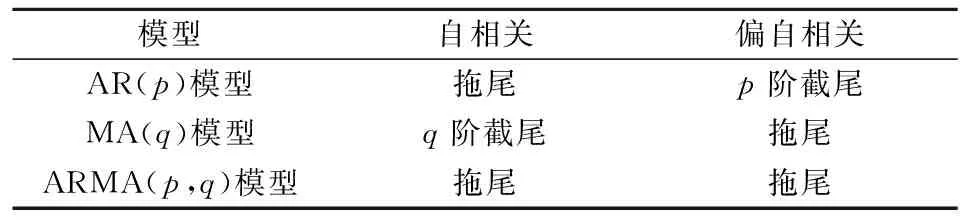
表3 模型选定方法

由表2可知,立靶密集度序列的自相关函数是拖尾的,而偏自相关函数是截尾的。则通过表3可以判断,原序列的模型为AR(5),立靶密集度数据的建模结果为

3 模型比较与验证

比较AR(1)模型与AR(5)模型的残差,其自相关与偏自相关如表4、表5所示。

表4 AR(1)模型残差的自相关与偏自相关

表5 AR(5)模型残差的自相关与偏自相关

比较自相关函数可以看出:一阶模型的残差依然具有较为明显的相关性,与白噪声相比有比较大的差别;而AR(5)模型的残差则可认为是白噪声。同时比较残差的方差,后者更小。分别用一阶模型和本文模型进行预测,结果如表6所示。其中,X表示测量值;X1,X2分别表示AR(1)模型和AR(5)模型的预测值;e1,e2分别表示AR(1)模型和AR(5)模型的预测误差。

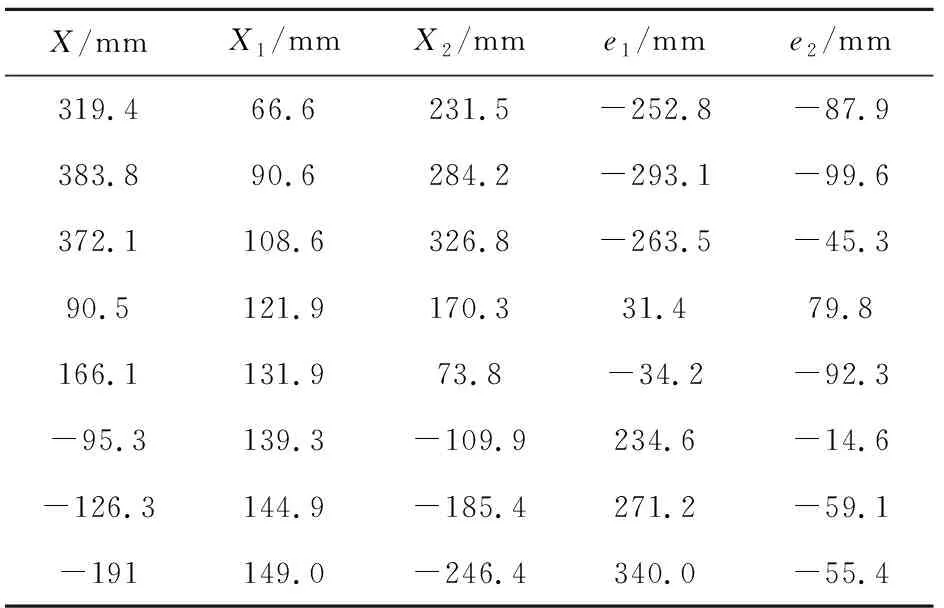
表6 模型验证结果

比较AR(1)模型与AR(5)模型的预测误差,后者的方差更小,结合模型残差的比较结果,本文的模型比一阶模型更为准确。

4 结论

战斗炮的立靶密集度是武器系统射击精度的重要组成部分,在传统武器系统射击效力分析中,通常假定其为平稳不相关误差。随着火炮射速的提高,火炮冲击载荷所带来的弱相关误差已不能被忽略,其通常用一阶模型来表示。本文将时间序列分析引入立靶密集度序列分析,对实测数据建立了高阶模型。比较两者的拟合残差以及预测误差,结果证明了用一阶模型来描述脱靶量数据精度欠佳,而本文的模型则更为准确,为更好地分析武器系统射击效力奠定了基础。

[1] 杨维佳.可用于单发或连发射击时的立靶密集度测量[J].弹道学报,1990,2(1):43-47.

YANG Wei-jia.The density measurement of vertical target used for single shot or rapid fire[J].Journal of Ballistics,1990,2(1):43-47.(in Chinese)

[2] 王宝元,衡刚,周发明,等.火炮立靶密集度测量方法[J].测试技术学报,2011,25(6):529-535.

WANG Bao-yuan,HENG Gang,ZHOU Fa-ming,et al.The measurement methods for vertical target dispersion of gun[J].Journal of Test and Measurement Technology,2011,25(6):529-535.(in Chinese)

[3] 李笑娟,徐向毅.高射速火炮带弹序立靶密集度测试技术研究与实践[J].火炮发射与控制学报,2011(3):71-73.

LI Xiao-juan,XU Xiang-yi.Study and practice of vertical target density test technology with target-hitting sequence calculation[J].Journal of Gun Launch & Control,2011(3):71-73.(in Chinese)

[4] 郭锡福.连发武器立靶密集度分析[J].弹箭与制导学报,1987(1):32-35.

GUO Xi-fu.The density analysis of vertical target used for rapid fire[J].Journal of Projectiles,Rockets,Missiles and Guidance,1987(1):32-35.(in Chinese)

[5] 姚志军,朱凯,王军,等.速射火炮立靶密集度的相关系数分析与检测[J].火炮发射与控制学报,2012(2):1-4.

YAO Zhi-jun,ZHU Kai,WANG Jun,et al.Analysis and detection for correlation coefficient of rapid-fire gun’s vertical target density[J].Journal of Gun Launch & Control,2012(2):1-4.(in Chinese)

[6] 安鸿志,陈兆国,杜金观,等.时间序列的分析与应用[M].北京:科学出版社,1983.

AN Hong-zhi,CHEN Zhao-guo,DU Jin-guan,et al.Analysis and application of time series[M].Beijing:Science Press,1983.(in Chinese)

[7] 丁明,张立军,吴义纯.基于时间序列分析的风电场风速预测模型[J].电力自动化设备,2005,25(8):32-34.

DING Ming,ZHANG Li-jun,WU Yi-chun.Research on wind speed prediction of the wind farm based on time series method[J].Electric Power Automation Equipment,2005,25(8):32-34.(in Chinese)

[8] DICKEY D A,FULLER W A.Likelihood ratio statistics for autoregressive time series with a unit root[J].Journal of the Econometric Society,1981,49(4):1 057-1 072.

[9] 易丹辉.数据分析与EVIEWS应用[M].北京:中国统计出版社,2002.

YI Dan-hui.Data analysis and EVIEWS application[M].Beijing:China Statistics Press,2002.(in Chinese)