炮弹三维密集度指标体系研究
卢国胜,郭尚生
(1.中国人民解放军驻七二四厂军事代表室,沈阳 110045;2.辽沈工业集团有限公司,沈阳 110045)
目前,炮弹密集度指标都是以二维坐标给定和检查,对于地面压制性作战,火炮可以基本满足论证研制、生产制造、检验验收和作战指挥的需求,但对在空中引爆开舱的照明弹、侦察弹和对空中目标作战的榴弹,以及用时间引信空中引爆后对地面目标作用的炮弹,用二维坐标考核密集度就显得不准确、不直观和不方便。为了解决目前炮弹密集度指标都以二维坐标给出并考核的不足,通过对目标特性进行剖析,对各类炮弹终点效应进行分析,在概率论的基础上,本文研究建立三维密集度指标体系的理论基础和考核方法,为炮弹在论证、制造、检验和作战指挥中快速、精确使用密集度指标提供了理论基础。
三维密集度指标体系可以解决二维密集度指标体系的不足,同时,由于计算机技术的成熟应用,三维指标体系可以更精确、更快速完成射击诸元的指挥、装定和修正。
1 三维密集度指标体系的建立
炸点密集度散布一般服从正态分布,在各个方向上互不相关,可由n维分布规律进行推导[1-2]。
相互独立的三维正态分布的边际密度为
式中:σm为各维的散布方差,μm为各维的散布中心,xm为各维的落点,下标m代表x,y,z。
相互独立的三维正态分布的联合密度为
f(x,y,z)=f1(x)f2(y)f3(z)=
则有相互独立的三维正态分布的联合分布函数为
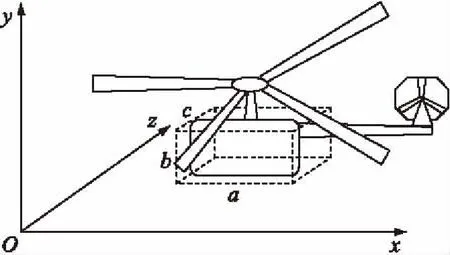
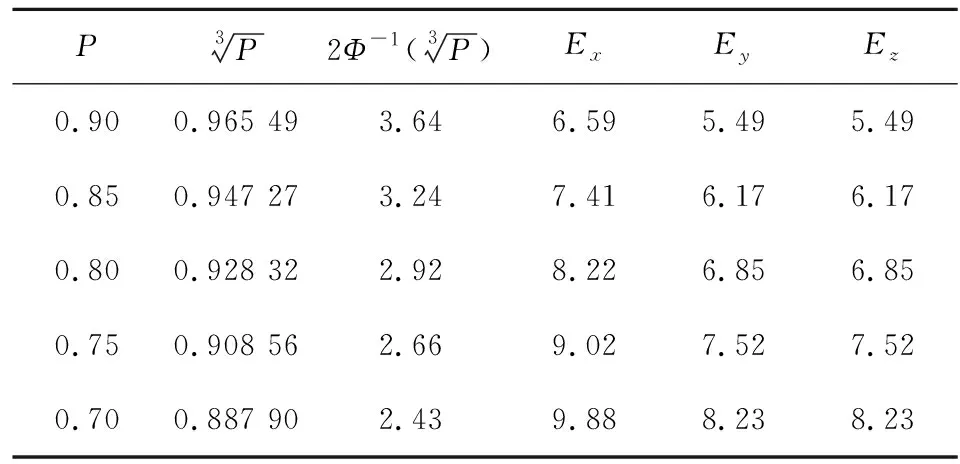
F(-a1 (3) 相互独立的三维正态分布的概率分布由其联合分布函数确定[3],即: P{-a1 (4) 炮弹在空中引爆,一是直接对空作战,如毁伤飞机、导弹、投放物;二是在空中引爆后作用于地面目标,如实施照明、发烟,以及子母弹子弹对地面目标作用、未敏弹子弹对地面目标作用等。后者对目标作用可借用普通炮弹的二维密集度形式,但需要考虑等效计算的算法和精确度;前者对目标作用的炸点散布,需要进一步对其作用要求和考核方法进行研究。首先,要确定目标空间大小,找到炮弹对目标作用可靠性的分布规律;其次,要明确作战时对目标的命中概率要求,据此计算出弹丸在空中炸点散布密集度的指标要求。 例,某榴弹需要用于打击3 000~5 000 m处,几十m至数百m高度的武装直升机目标。假设目标为矩形立方体,如图1所示,并且射弹的空中炸点为三维球形散布,服从正态分布,并各自独立,则可由式(3)、式(4)推出命中目标的概率: 式中:a,b,c分别为立方体目标的长、高、宽;Ex为发射系统的纵向中间误差值;Ey为发射系统的高度中间误差值;Ez为发射系统的横向中间误差值;Φ为标准正态分布函数。 图1 空中目标示意图 当a,b,c比较接近时,可以用以下公式近似计算: 式中:P为命中目标的概率,Φ-1为Φ的反函数。 当a=24 m,b=20 m,c=20 m,Em与P的关系如表1所示。 表1 计算实例得到的Em与P的关系 炮弹战技指标E0与瞄手误差Er(瞄手误差值包括除炮弹本身造成的误差以外的系统误差)的关系为[1] 若取瞄手误差Er=0.6 m(按2密位计算),命中概率P=0.9,则该弹在3 000 m处的三维密集度指标应是:Ex0=6.56 m,Ey0=5.46 m,Ez0=5.46 m。 用单台测量仪器进行单点测量,一次记录3项数据,分别是测点与炸点的距离Li,炸点相对测点方向角αi,炸点相对测点高低角βi。 事先确定测点坐标A(xA,yA,zA),则测点坐标可由以下公式计算: xi=Licosβisinαi+xA (10) yi=Lisinβi+yA (11) zi=Licosβicosαi+zA (12) 式中:xi,yi,zi为一组试验数据中第i发的三维落点坐标值。 用2台测量仪器进行两点测量,如图2所示,A、B两点为仪器测量点,P点为炮弹炸点。一次记录4项数据,分别是第1测点方向角αAi,第2测点方向角αBi,第1测点高低角βAi,第2测点高低角βBi。 图2 炸点三坐标示意图 先确定第1测点坐标A(xA,yA,zA)和第2测点坐标B(xB,yB,zB),并使yB=yA,zB=zA,则所测炸点坐标为 对于炮弹装备产品建立三维密集度指标体系在理论和实践上都是可行的,也是必要的。本文建立的三维密集度指标体系可以解决二维密集度指标体系的不足,同时包容各类炮弹满足论证、设计、考核和使用的要求。通过三维密集度指标体系的建模,可以充分应用计算机技术,使密集度指标体系可以更精确、更快速完成各类炮弹的射击诸元的指挥、装定和修正,提高战术技术指标的实用性。 [1] 姚平中,韩之俊.概率与统计[M].南京:华东工程学院,1983. YAO Ping-zhong,HAN Zhi-jun.Probability and statistics[M].Nanjing:Huadong Engineering College,1983.(in Chinese) [2] 德沃尔 J L.概率与统计(理工类)[M].北京:机械工业出版社,2005. DEVORE J L.Probability and statistics for engineering and the sciences[M].Beijing:China Machine Press,2005.(in Chinese) [3] 马振华.概率统计与随机过程[M].北京:清华大学出版社,2005. MA Zhen-hua.Probability and statistics and stochastic process[M].Beijing:Tsinghua University Press,2005.(in Chinese)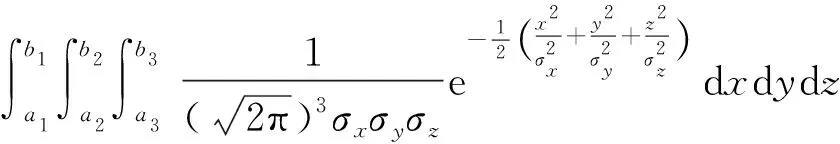
F(az,bx,by)]+[F(ax,ay,bz)+F(ax,az,by)+
F(ay,az,bz)]-F(ax,ay,az)2 空中目标密集度要求的分析
2.1 目标命中要求
2.2 计算实例
3 三维密集度指标的考核
3.1 单点测量三坐标
3.2 两点测量三坐标

4 结束语

