轴对称超空泡流振动频率特性

安 海,蒋运华,安伟光

(哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001)

超空泡减阻技术的应用可以使水下运动体的摩擦阻力大大降低,为水下高速运动提供不可或缺的条件。而保证超空泡减阻的一个重要条件就是空泡的稳定性,稳定的空泡流可以使航行体阻力大大减小,不稳定的空泡则会对航行体造成损害。空泡稳定性的问题直接关系到水下高速运动体的受力状态与运动的稳定性。因此,研究空泡的稳定性具有重要的意义。

目前,针对超空泡的稳定性已经开展了许多相关的研究工作。Serebryakov[1]基于细长体理论和诱导模型,提出一种水下高速运动体轴对称超空泡流实用的计算方法。Semenenko[2]通过动量定理得到了由重力效应引起的自然空泡轴线变形的计算公式。Buyvol[3]得出了重力效应对空泡截面变形影响的判别准则。张学伟等[4-7]对自然超空泡进行了数值仿真的研究,得出流场压力、模型速度、模型后体和空化器阻力系数都会对通气超空泡形态稳定性产生影响。并且通过实验手段对超空泡形态及稳定性进行研究,得出了重力对空泡形态的影响,以及空泡失稳的3种方式。蒋运华、安伟光等[8]依据空泡不同闭合形式的气体泄漏规则和通气系统,建立了空泡内气体的平衡方程,给出用于计算运动体姿态的动力学方程,分析了局部空泡及超空泡航行状态的受力特性。张纪华等[9]用仿真的方法研究了内压扰动对非定常空泡形态的影响。冯雪梅等[10]研究了轴对称模型上的通气空泡和自然空泡的振荡特性。上述文献的研究方法都是通过Logvinovich独立扩张原理[11]建立分析模型,再进行研究。本文从Logvinovich独立扩张原理出发,建立描述空泡流动的微分方程,通过线性化处理得到关于空泡内压的微振方程,由空泡体积与空泡内压力的函数关系可知,空泡形态的稳定与压力相关,压力振动的发散将导致空泡形态的不稳定。

1 轴对称空泡的动力学模型

1.1 空泡流的状态和参数假定

图1 航行体空化器观察平面

1.2 空泡截面的扩张方程

根据Logvinovich独立原理,可有

式中:ρ为液体密度,假设它不随时间而改变;k=k(σ),即k是关于空化数σ的函数,在本文中假设k为常数;Δp(x,t)=p∞-pc(x,t)。p∞为物体前方未扰动处液流静压,pc(x,t)为空泡内压力。

由于空化器经过任意平面时为t1时刻,于是对式(1)积分可得:

1.3 空泡内部气体方程

空泡内气体的体积表达式为

(4)

空泡内部气体质量的变化方程为

整理得:

式中:n是一个和热力学过程有关的系数,在绝热情况下可取n=1,于是可以得到:

1.4 描述空泡系统的微分方程

假设在整个流动过程中液体p∞保持不变,即液体总压力保持不变;假设任意时刻空泡内的压力pc处处相等,即空泡内的压力仅是时间的函数:pc=pc(t),于是可得压差:

Δp(x,t)=p∞-pc(t)

(8)

由式(4)可以得到:

(9)

(10)

对式(10)两边求导,得:

由于空泡长度L仅与空化器的位移H(t)有关,是空化器位移H(t)的一元函数,于是由全微分的形式不变性可得:

于是

由式(12)、式(13)可得:

对式(14)两边再求导一次,得:

根据式(1)和式(8)可得:

由式(2)易得:

进而可以得到空泡流系统的微分方程:

2 方程的特殊化和线性化处理

2.1 特殊化处理

2.2 线性化处理

取pc0,Q0,L0,τ0为稳态值,δpc,δQ,δL,δτ为脉动值,于是

根据式(19)可得:

略去二阶无穷小量便得:

nQ0(δpc)+(δQ)pc0=0

两边同时除以δt,便有:

将式(21)两边再对时间求导,可得:

其中,

于是有:

(24)

根据式(18)和式(23),可得:

(25)

再将式(24)代入式(25),整理可得:

将式(26)代入式(22)并整理可得空泡压力的振动方程:

(28)

为了得到一般性的结论,将式(28)中的参数换成无量纲参数。由振动方程的特点,可令pc(t)=eλt,pc(t/T)=eλ(t/T),于是有:

将式(30)化简便得到振动的特征方程:

再令

通过整理可得:

由于

因此有

下面将要求的是μ和ω的边界条件。将λ=μ+jω代入式(32)可以得到:

由参考文献[11]知,在空泡内无后体时有

3 计算结果与比较

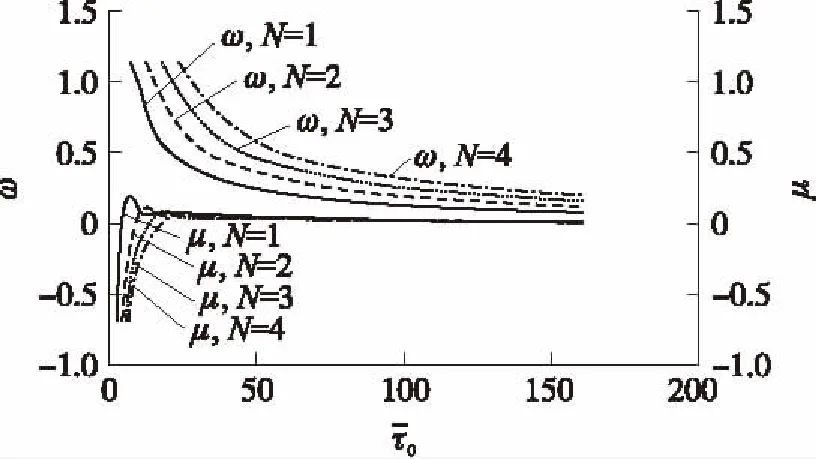
图2 μ和ω随变化的规律

于是得:

再由β的定义可知,在通气超空泡流动中一般β>1,于是得空泡内无后体情况下、稳定状态时的动力学相似参数β的取值范围:

1<β<2.645

综上所述,可得出如下结论:

①可以将动力学相似参数β作为判定超空泡中气体振荡稳定性的一个标准。

②当1<β<2.645时,空泡是稳定的;当β>2.645时,空泡振荡将会发散;β=2.645是空泡稳定的一个临界值。

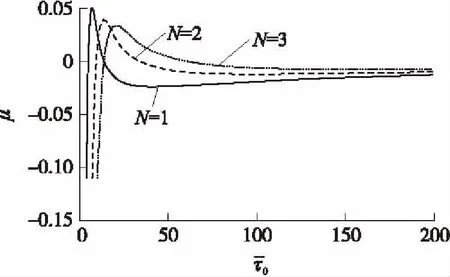
图3 文献[13]中μ随变化的规律

4 结论

针对空泡振动方程,提出了一种新的求解空泡稳定性判定标准的动力学相似参数β的取值范围的方法。该方法针对复杂超空泡系统的微分方程求解困难的问题,对方程做了特殊化处理,进一步采用线性化手段,通过软件仿真,得到空泡振动频率特性以及稳定性量化条件。提供了一种研究轴对称超空泡流稳定性的一般性方法,为工程研究提供有益的参考。

该方法主要应用于超空泡流动在100 m/s左右的情况。对于超高速射弹,其速度接近水中声速(1 470 m/s),流体压缩效应会对空泡形态产生影响;另外,对于人工充气情况,Fr数变小,有后体空泡对空化数的变化更加敏感,从而增加了稳定控制的难度。

[1] SEREBRYAKOV V V.Practical methods for calculation of supercavitation on axisymmetric bodies for high speed motion in water[C]//Proceedings of the ASME Fluids Engineering Division Summer Conference 2009,USA:FEDSM,2009:393-400.

[2] SEMENENKO V N.Calculations of the 2D supercavity shape under harmonic perturbations[J].International Journal of Fluid Mechanics Research,2001,28(5):673-682.

[3] BUYVOL V N.Slender cavities in flows with perturbations[M].Kiey:Naukova Dumka Publishing House,1980.(in Russian)

[4] 张学伟,张亮.自然超空泡形态稳定性的数值仿真[J].弹道学报,2009,21(2):103-110.

ZHANG Xue-wei,ZHANG Liang.Numerical simulation of shape stability of natural supercavitation[J].Journal of Ballistics,2009,21(2):103-110.(in Chinese)

[5] 张学伟,张亮.通气超空泡稳定性分析的一种数值算法[J].力学学报,2008,40(6):820-825.

ZHANG Xue-wei,ZHANG Liang.A numerical method for the stability analysis of ventilated supercavity[J].Chinese Journal of Theoretical and Applied Mechanics,2008,40(6):820-825.(in Chinese)

[6] 张学伟,张亮.通气超空泡形态稳定性的数值模拟研究[J].计算力学学报,2010,27(1):76-81.

ZHANG Xue-wei,ZHANG Liang.Numerical simulation of the shape stability of ventilated supercavity[J].Chinese Journal of Computational Mechanics,2010,27(1):76-81.(in Chinese)

[7] 张学伟,张嘉钟,王聪,等.通气超空泡形态及其稳定性实验研究[J].哈尔滨工程大学学报,2007,28(4):381-387.

ZHANG Xue-wei,ZHANG Jia-zhong,WANG Cong,et al.Experimental research on ventilated cavitation and its stability[J].Journal of Harbin Engineering University,2007,28(4):381-387.(in Chinese)

[8] 蒋运华,安伟光,安海.超空泡运动体通气加速阶段非定常过程研究[J].弹道学报,2011,23(2):67-71.

JIANG Yun-hua,AN Wei-guang,AN Hai.Study on unsteady process of ventilation accelerated motion stage for supercavitating vehicle[J].Journal of Ballistics,2011,23(2):67-71.(in Chinese)

[9] 张纪华,张宇文,李雨田.内压扰动对非定常空泡形态的影响[J].弹道学报,2012,24(1):88-91.

ZHANG Ji-hua,ZHANG Yu-wen,LI Yu-tian.Effect of internal pressure perturbation on unsteady cavity form[J].Journal of Ballistics,2012,24(1):88-91.(in Chinese)

[10] FENG Xue-mei,LU Chuan-jing,HU Tian-qun.The fluctuation characteristics of natural and ventilated cavities on an axisymmetric body[J].Journal of Hydrodynamics(Ser.B),2005,17(1):87-91.

[11] LOGVINOVICH G V.Hydrodynamics of flows with free boundaries[M].Kiev:Naukova Dumka,1969:215.(in Russian)

[12] PARYSHEV E V.Approximate mathematical models in high-speed hydrodynamics[J].Journal of Engineering Mathematics,2006,55(1):41-64.

[13] 陈伟政.轴对称超空泡流稳定性分析[J].船舶力学,2006,10(1):1-6.

CHEN Wei-zheng.Stability analysis of unsteady axisymmetric super-cavity flows[J].Journal of Ship Mechanics,2006,10(1):1-6.(in Chinese)