混合目标火力分配及弹药消耗量求解方法

宋谢恩,宋卫东,赵成旺,2,佟德飞

(1.军械工程学院 火炮工程系,石家庄,050003;2.南京炮兵学院 廊坊校区,河北 廊坊,065000)

火箭炮作为面杀伤性武器,常用来打击压制大面积集群目标,如集群有生力量、高技术武器系统、防御工事建筑[1]等。集群目标多数情况下为混合目标,较为典型的如有生力量、装甲车辆和防御工事组成的混合目标。

火箭炮射击的火力分配方案设计和弹药消耗量求解对于实际作战有着重要意义。文献[2]采用一定的火力分配流程和算法,分析了点线面目标的火力分配;文献[3]基于小生境遗传算法和模糊多目标决策提出了一种混合算法用以解决多指标下的火力分配问题;文献[4]统一出一个共同的表示形式,并导出了毁伤目标所需平均消耗量的公式;文献[5]详细介绍了制导火箭炮弹药消耗量计算流程和计算模型。

以往文献提出的射击分配方案以及弹药消耗量求解方法和模型多以单一目标为射击对象,较少涉及混合目标,与实际作战运用有较大差距。本文基于火箭炮射击学、毁伤理论和最优化原理,提出了混合目标的射击火力分配和弹药消耗计算模型,为实战射击和弹药预测提供了参考。

1 单一目标火力分配与毁伤计算

1.1 均匀分布法毁伤概率计算模型

火力分配和弹药消耗的计算是建立在毁伤概率计算模型的基础之上的。火力分配是指瞄准点的选取[6],其目标函数即为毁伤概率函数;弹药消耗计算其实质就是毁伤概率求解的逆运算[7],但在实际计算中可以转化为弹药量递增的火力分配问题,详见最小弹药消耗量求解。

本文采用均匀分布法计算毁伤概率[8]:

(2)

式中:a1=0.070 523 078 4,a2=0.042 282 012 3,a3=0.009 270 527 2,a4=0.000 152 014 3,a5=0.000 276 567 2,a6=0.000 043 638;ρ为炮兵常数,ρ=0.476 9[9]。

1.2 单一目标最有利火力分配

单一目标的最有利火力分配求解也是混合目标最优火力分配和最小弹药消耗计算的基础。对于单一目标而言,为取得最大毁伤效果,需要按照最有利火力方案进行射击参数配置[6],本模型根据现有火箭炮营装备配置情况,行3标尺6方向分划射击,射击的距离差和射向间隔计算如下。

表尺差:

方向差:

以上毁伤概率计算和火力分配模型仅适用于单一目标,对于混合目标则需要新的思路和方法。

2 混合目标火力分配计算

2.1 混合目标最优火力分配求解

射击完成后,混合目标各目标的毁伤率是不同的,对于混合目标整体的毁伤情况没有相应的数值表征。本文基于加权平均的思想,提出综合毁伤率的概念,其计算方法为

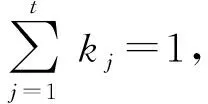
在给定弹药量N和毁伤率任务要求的情况下,对于混合目标求解最优火力分配方案,按照以下步骤进行:以目标j为基准目标,按照单一目标最有利火力分配得出射击的表尺差hj和方向差ij,求解目标j的毁伤率,再以得到的hj,ij为分配方案求解其它目标的毁伤情况。更换基准目标重复以上计算,得出t种基准目标下各目标的毁伤情况。若方案中仅有一种满足毁伤率要求,即为最优火力分配方案;若2种及以上都满足要求,则综合毁伤率最大的即为最优火力分配方案。详细流程见图1。

图1 混合目标最优火力分配方案流程

2.2 计算求解

混合目标幅员为600 m×600 m,暴露立姿步兵、轻型装甲车辆、火力点掩体(步兵对应j=1、车辆对应j=2、掩体对应j=3)均匀分布在其幅员内,火箭炮对其毁伤幅员S分别为800 m2,80 m2,25 m2,毁伤目标所需的平均命中弹数ω分别为1,1,2;毁伤率任务要求为P1,P2,P3。以步兵基准目标求得的火力方案为方案1,相应地,车辆、掩体分别对应方案2、方案3。某型火箭炮兵营下辖3个连,每连6门炮车,营射击诸元误差Ed=74 m,Ef=26 m,散布误差Bd=106 m,Bf=58 m。实际需要解决的问题是:给定弹药量,求解最优火力分配方案以满足各目标的毁伤要求。

给定弹药量N=1 440,按照上述流程求解,如表1所示。

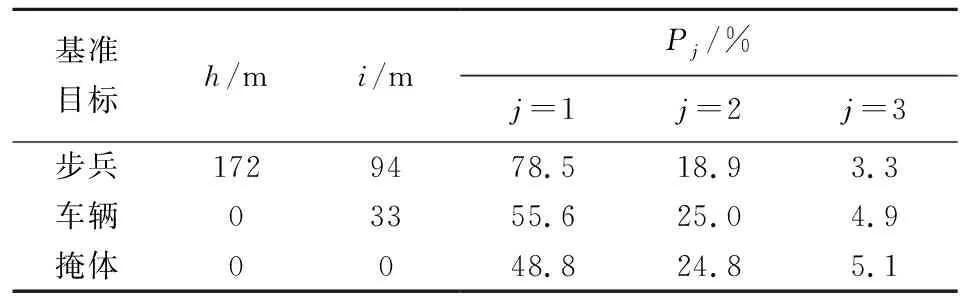
表1 不同火力分配方案对比

若任务要求为P1=40%,P2=10%,P3=5%,则只有方案3(j=3)可以实现。

若P1=40%，P2=10%，P3=2%,则3种方案都可以实现。若3种目标是等权重的,则平均毁伤率P=(P1+P2+P3)/3,分别为33.5%,28.5%,26.2%,第1种方案最优[10];若步兵、车辆、掩体权重分别为0.1,0.8,0.1,则综合毁伤率P=0.1P1+0.8P2+0.1P3,分别为23.3%,26.1%,25.2%,第2种方案最优。

3 混合目标最小弹药消耗量求解

混合目标的最小弹药消耗量求解方法与最优火力分配求解的思路是一样的,具体流程如图2所示。

图2 混合目标最小弹药消耗量求解流程

不给定弹药消耗量,其他计算条件与火力分配求解中相同,按照上述流程计算可得不同基准目标下的弹药消耗量,如表2所示。

表2 不同基准目标下的弹药消耗量

由以上3组毁伤率要求和计算结果可以看出,第1组步兵毁伤率均为50%,第2组车辆均为30%,第3组掩体均为5%,都是刚满足作战要求。由此可认为,作战要求中总有一个指标是所有要求中较难满足的;当较难目标满足时,其他目标一定能满足。故得出,只要出现某一基准目标的单一目标最小弹药消耗量满足其他的目标毁伤率要求,即为混合目标的最小弹药消耗量。以此为依据,对求解流程做出修改,如图3所示。

图3 混合目标最小弹药消耗量求解流程改进

修改后的计算程序加入了判断,不用计算出所有基准的用弹量就能够判断出哪种基准用弹量最小,避免了没有效果的运算,加快了运算速度。

4 结论

混合目标的最优火力分配方案能够满足混合目标中各目标的毁伤要求,有重点地进行火力分配,使综合毁伤率达到最大。最小弹药量求解为混合目标作战的弹药需求量预测提供了计算方法,使火箭炮的弹药准备量更精准。

考虑目标特性进行火力分配和弹药消耗预测是实现有效打击的前提。本文提出的计算模型,考虑了混合目标中不同目标作战参数的不同,实现了对于混合目标的最优火力分配方案和最小弹药消耗量的求解,能够为实际作战中火箭炮打击混合目标提供理论基础。

[1] 李新龙.多管火箭武器系统及其效能[M].北京:国防工业出版社,2008.

LI Xin-long.Multiple rocket weapon system and its effectiveness[M].Beijing:National Defense Industry Press,2008.(in Chinese)

[2] 李晓婷,张玉梅,吴琼.火箭炮多目标射击任务中火力分配模型及算法[J].火力与指挥控制,2012,37(增刊):44-46.

LI Xiao-ting,ZHANG Yu-mei,WU Qiong.The firing distribution model and algorithm in multi-target firing task

of rocket[J].Fir Control & Command Control,2012,37(supplement):44-46.(in Chinese)

[3] 朱小操,于兰欣.多指标下的炮兵火力最优分配[J].指挥控制与仿真,2007,29(3):65-68.

ZHU Xiao-cao,YU Lan-xin.Artillery fire optimal distribution in multi-index[J].Command Control & Simulation,2007,29(3):65-68.(in Chinese)

[4] 刘力维,郭治.地面火炮毁伤目标的弹药消耗量[J].南京理工大学学报,2003,27(4):367-370.

LIU Li-wei,GUO Zhi.Ammunition consumption for a ground cannon to kill a target[J].Journal of Nanjing University of Science and Technology,2003,27(4):367-370.(in Chinese)

[5] 李晓婷,张玉梅,吴琼.制导火箭炮弹药消耗量模型[J].电脑开发与应用,2013,26(5):71-72,75.

LI Xiao-ting,ZHANG Yu-mei,WU Qiong.Ammunition consumption model of guided rocket projectile[J].Computer Development & Applications,2013,26(5):71-72,75.(in Chinese)

[6] 江华.炮兵射击基本理论分析[M].北京:兵器工业出版社,2004.

JIANG Hua.Basic theory of artillery shoot analysis[M].Beijing: Ordnance Industry Press,2004.(in Chinese)

[7] 李学起,汪德虎,关庆云,等.舰炮对敌野战炮兵连射击效果实时评估[J].火力与指挥控制,2010,35(6): 137-139,143.

LI Xue-qi,WANG De-hu,GUAN Qing-yun,et al.Evaluation of ship gun’s fire effect to fieldpiece company[J].Fire Control & Command Control,2010,35(6): 137-139,143.(in Chinese)

[8] 李质明.炮兵射击理论[M].长沙: 国防科技大学出版社,2003.

LI Zhi-ming.Artillery shooting theory[M].Changsha: National University of Defense Technology Press,2003.(in Chinese)

[9] 张平乐.炮兵射击效率评定(试用)[M].宣化:炮兵指挥学院,2006.

ZHANG Ping-le.Evaluation of artillery fire efficiency(trial)[M].Xuanhua: Artillery Command College,2006.(in Chinese)

[10] 赵敬宝,李斌,吴映军,等.炮兵火力打击决策方案优选的方法[J].弹道学报,2005,17(4): 79-83.

ZHAO Jing-bao,LI Bin,WU Ying-jun,et al.An optimum seeking method of decision for artillery strike[J].Journal of Ballistics,2005,17(4): 79-83(in Chinese)