重复使用运载器的制导与控制一体化设计研究

王谦，李新国

(西北工业大学航天学院，陕西西安710072)

0 引言

重复使用运载器是指单级或多级入轨、跨大气层飞行、并且可以重复使用的飞行器。作为新一代的天地往返运输系统，重复使用运载器需要能够快速准备和发射，并可以完成卫星发射、高空侦察以及全球快速打击等多种任务，因此快速有效的制导与控制系统的设计就成为重复使用运载器研制中的一项关键技术。

近年来，国内外对重复使用运载器的制导与控制方法已经展开了广泛的研究。总结相关研究成果可以发现，其研究重点主要集中在提出快速精确的弹道优化及制导指令生成算法，以及高效且鲁棒性好的姿态控制算法［1-4］。这是因为对于当前火箭等运载器，其制导系统与控制系统是分开设计，然后再进行联合调试。对于这种设计流程，其可行性在火箭上升段及飞船再入段等实际应用中已经被广泛验证。而对于下一代重复使用运载器，其气动特性、控制能力、任务特性等相对于传统运载器均有较大不同。

本文通过分析重复使用运载器的制导系统与控制系统之间的耦合关系，说明制导系统与控制系统分开设计的流程已经不适用于重复使用运载器，进而提出重复使用运载器的制导与控制一体化设计方法，并通过将一体化设计与三自由度弹道设计结果进行对比，表明了制导与控制一体化设计的必要性和有效性。

1 制导与控制一体化设计

1.1 制导与控制一体化概述

在火箭等传统运载器制导与控制系统的设计过程中，制导系统与控制系统的设计是分别进行的，如图1所示。

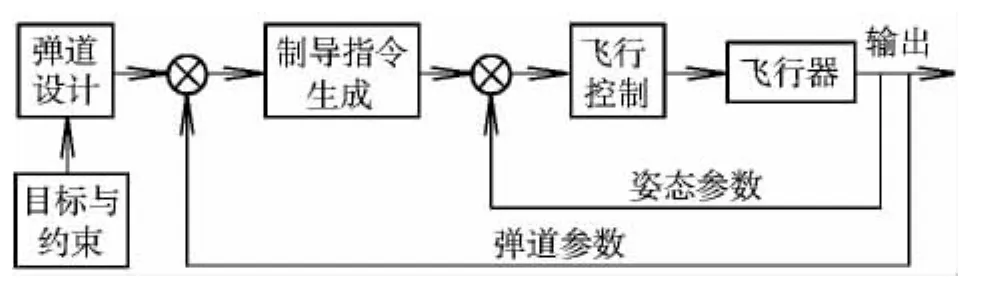
图1 传统的制导与控制系统Fig.1 Traditional guidance and control system

对于下一代重复使用运载器，不但需要执行多种灵活任务，而且两次发射之间的准备时间也应当尽可能短，传统的反复迭代的设计流程已经难以满足应用要求。为了获得高可靠性，重复使用运载器的制导系统与控制系统在故障条件下都需要有一定的重构能力，如果重构的过程也需要两套系统反复迭代，就会使得制导与控制系统重构难以满足实时性要求。对于下一代重复使用运载器，其气动特性、控制能力、任务特性等相对于传统运载器均有较大不同。例如，为了能够完成多种灵活任务和提升可靠性，重复使用运载器需要利用较多的舵面来获得机动能力，所以在运载器返回段的飞行中，其舵面偏转产生的气动力已经成为总气动力的重要部分。

图2为未考虑气动舵面造成的气动力，以及升降舵与副翼偏转角度均为15°时的总气动力对比。可见气动舵面的偏转相当于改变了运载器的气动特性，而传统的弹道设计与优化方法运用的只是机身部分的气动参数，加上舵面产生的气动力之后，可能会使得弹道设计的结果并非最优解，甚至无法满足某些约束条件。

图2 考虑舵面偏转的气动力系数Fig.2 Aerodynamic force concerning control surface deflection

图3 给出了X-33飞行器的某一再入过程中舵面所产生的气动力在总气动力中所占的比重。可以看出，舵面产生的轴向力与法向力达到总气动力的20%左右，已经成为总气动力的重要组成部分，而且这个比重的大小与气动舵面偏转角度，即控制策略有直接关系。

图3 舵面产生的气动力在总气动力中的比重Fig.3 Proportion of the aerodynamic force of control surface in the total aerodynamic force

鉴于上述制导与控制系统设计流程的不足，针对重复使用运载器建立起制导系统与控制系统的一体化设计方法就十分必要。但是对于重复使用运载器，其制导与控制一体化设计的文献却较少［4-6］。

本文尝试运用最优控制方法，对重复使用运载器的制导与控制系统进行一体化分析与初步设计。如图

4所示，在一体化设计的重复使用运载器制导与控制系统中，弹道设计、制导指令生成以及控制系统不再分开进行，而是由一体化制导与控制系统完成所有工作，即一体化制导与控制系统的输出直接为舵面偏转角度和RCS工作指令，从而不再有显式的标准弹道与制导指令。这样将弹道设计算法、制导指令生成算法以及控制算法集合为同一问题进行分析与设计，可以有效避免制导系统与控制系统不能良好匹配的可能性，从而增强重复使用运载器的可靠性。

1.2 制导与控制一体化设计

考虑圆球形大地下的重复使用运载器的六自由度模型:

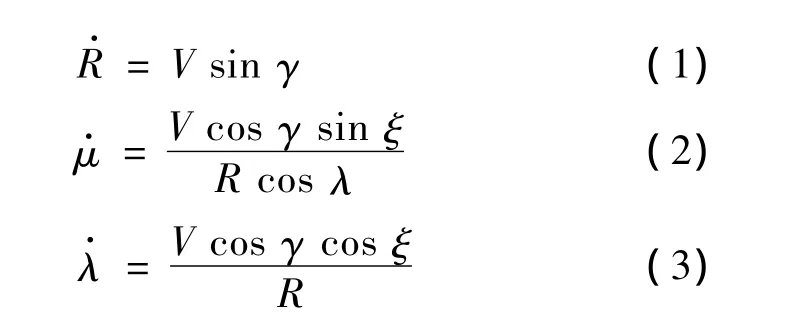
式中，R，μ，λ，V，γ，ξ分别为地心距、经度、纬度、空速、弹道倾角以及弹道偏角;p，q，r分别为机体 x，y，z轴转动角速度;φ，θ，ψ分别为滚转角、俯仰角以及偏航角;L，D，Y 分别为机体 x，y，z轴所受的升力、阻力和侧力;Ml，Mm，Mn分别为机体 x，y，z轴所受的总力矩。运用最优化方法设计一体化制导与控制系统，将式(1)～式(12)作为状态方程，飞行器控制变量δ作为输入变量，并根据任务要求确定状态与路径约束以及指标函数。以X-33重复使用运载器的返回段为例，运用只考虑机身气动力的三自由度弹道优化方法进行弹道设计时，其控制变量为迎角和速度滚转角:δ=［α，σ］。而运用制导与控制一体化设计时，其控制变量为气动舵面偏转角度:

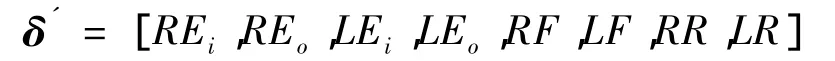
式中，REi，REo分别指右侧机身内、外侧升降舵;LEi，LEo分别指左侧机身内、外侧升降舵;RF，LF分别指右、左侧副翼;RR，LR分别指右、左侧方向舵。路径约束有过载、动压与热流:

再入初始及终端状态如表1所示。

表1 再入初始与终端条件Table 1 Initial and ending conditions of entry

本文采用高斯伪谱法和SNOPT序列二次规划求解器对上述最优控制问题进行求解。高斯伪谱法是一种最优控制问题的离散化方法，其基本原理为:对各状态及控制变量进行归一化，之后在时域的(－1，1)内选择Legendre-Gauss(LG)点作为配点，通过将LG点与初始和终端各变量的值共同构成最优控制问题的离散点，可以将各状态变量与控制变量在这些点上进行离散化。通过在离散点上构造Largrange插值多项式可以对全局的状态变量及控制变量进行逼近，而离散点处状态变量的导数可以用构造出的Largrange插值多项式的导数进行近似，从而将微分方程的约束转化为代数约束，原始的最优控制问题也就转化为非线性规划问题［7］，利用SNOPT等非线性规划求解器便可以对该问题进行求解。

2 仿真结果及分析

本文以X-33重复使用运载器为例，给出其制导与控制一体化设计结果，并将该结果与相同目标及约束条件下不考虑控制影响的弹道设计结果进行对比。

对于制导系统与控制系统分开设计的流程，需要首先设计和优化标准弹道，进而给出制导指令，然后得出控制指令，而一体化的制导与控制系统设计可以直接得出最优弹道以及跟踪该弹道需要的舵面偏转指令。对于X-33飞行器的返回段，其气动参数见文献［8］，状态方程为式(1)～式(12)、初始与终端条件见表1。下面以最大纵程与最大横程两种典型目标下的仿真结果为例，将制导与控制一体化设计结果与三自由度设计结果进行对比。

图5为最大纵程目标函数下优化得到的舵面偏转角度，最优弹道为图6中一体化设计的弹道。从舵面偏转角度来看，由于重复使用运载器在返回段需要长时间保持大迎角，所以升降舵持续大角度偏转，这也是图3中舵面产生的气动力在总气动力中比重较大的原因。图6和图7分别为最大纵程与最大横程目标函数下制导与控制一体化设计与传统三自由度弹道设计方法得出的最优弹道。结果表明，在正常飞行条件下，由于控制系统的机动能力与配平能力可以满足需要，舵面偏转所产生的的气动力并未显著影响返回段的最优弹道。

图6 最大纵程弹道设计结果对比Fig.6 Optimum trajectory under the objective of max downrange

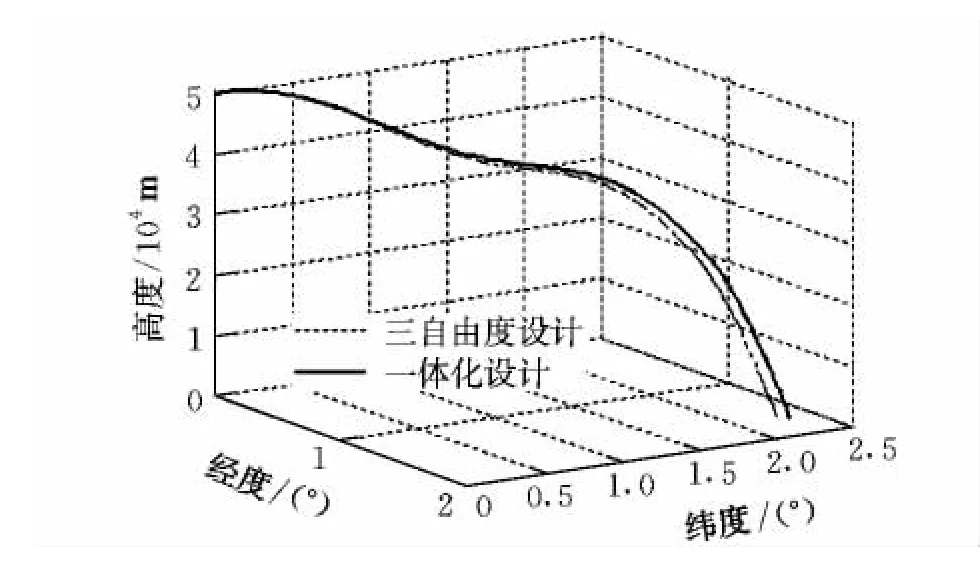
图7 最大横程弹道设计结果对比Fig.7 Optimum trajectory under the objective of max crossrange

图8 和图9显示出了右侧副翼卡死在－3°时，一体化设计与三自由度设计得出的弹道对比。

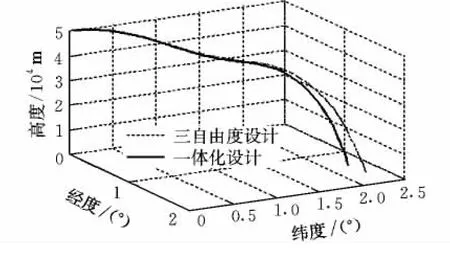
图8 最大横程弹道设计结果对比Fig.8 Optimum trajectory under the objective of max crossrange

图9 最大纵程弹道设计结果对比Fig.9 Optimum trajectory under the objective of max downrange

从仿真结果可以看出，当控制系统出现某些故障时，由于其配平能力和机动能力都有所降低，加之舵面偏转造成气动力的影响，使得忽略控制系统影响而设计的三自由度弹道有可能是运载器所无法实现的。所以，对于下一代的重复使用运载器，如果仍旧忽略舵面偏转造成的气动力设计和优化弹道，势必会影响弹道的最优性，在极端情况下甚至会影响任务的安全完成，对于重复使用运载器的制导与控制系统，一体化设计是必要的。

3 结束语

本文研究了重复使用运载器的制导系统与控制系统之间的耦合关系，并对一体化设计与三自由度弹道设计结果进行了对比。结果表明，二者的弹道优化结果在精度上存在一定差异，并且在故障条件下，制导与控制一体化设计能更准确地反映重复使用运载器的任务完成能力，从而提高运载器的可靠性。

［1］ Shen Z，Lu P.Onboard generation of three-dimensional constrained entry trajectories［J］.Journal of Guidance，Control，and Dynamics，2003，26(1):110-121.

［2］ Fahroo F，Ross I M.Direct trajectory optimization by a chebyshev pseudo spectral method［J］.Journal of Guidance，Control，and Dynamics，2002，25(1):160-166.

［3］ Doman D B，Ngo A D.Dynamic inversion-based adaptive/reconfigurable control of the X-33 on ascent［J］.Journal of Guidance，Control，and Dynamics，2002，25(2):257-284.

［4］ Schierman J D，Ward D G，Hall H R，et al.Integrated adaptive guidance and control for re-entry vehicle with flight-test results［J］.Journal of Guidance，Control，and Dynamics.2004，27(6):975-988.

［5］ Andrea Serrani，Zinnecker A M，Lisa Fiorentini，et al.Integrated adaptive guidance and control of constrained nonlinear air-breathing hypersonic vehicle models［C］//2009 American Control Conference.St.Louis，MO，USA，2009:3172-3177.

［6］ Shaffer P J.Optimal trajectory reconfiguration and retargeting for the X-33 reusable launch vehicle［D］.Naval Postgraduate School，Monterey，CA，USA，2004.

［7］ Garg D.Advances in global pseudo spectral methods for optimal control［D］.University of Florida，USA，2011.

［8］ Kevin P B.High-fidelity real-time trajectory optimization for reusable launch vehicles［D］.Naval Postgraduate School，Monterey，CA，USA，2006.