高超声速导弹近最优中制导律

乔清青，陈万春

(北京航空航天大学宇航学院，北京100191)

0 引言

高超声速导弹由于具有飞行高度高、速度快、机动性好等特点，能有效缩短对目标的反应时间，具有较高的突防成功率［1］。高超声速导弹飞行距离较远，需要一种中制导律将导弹导引至目标附近，为末端作战保存能量，满足各种约束条件，并完成中末制导的平滑交接班。

导弹的中制导问题可归结为一个非线性两点边值问题。由于导弹动力学系统的高度非线性，两点边值问题无法求出解析解。奇异摄动是解决复杂非线性最优控制问题的一种经典方法，通过抑制动力学方程中的小参数使系统阶数降低，可容易地获得相应的降阶解，再计算小参数获得边界层解，以修正降阶解。使用奇异摄动可得到性能较理想的近似解，并可根据需要获得开环或闭环解。奇异摄动方法在航空航天领域得到了广泛的应用。由于飞行器动力学方程中小参数不明显，因此通常使用“强迫奇异摄动”方法，即先根据估算的各变量的时间常数以及应用经验区分变化快慢不同的变量，再在快变量前插入小参数ε(0＜ε＜1)构成奇异摄动系统。令小参数为零，即假设较快变量能在瞬间达到平衡，从而使系统阶数降低，并求解出降阶解，然后通过边界层修正计算考虑被忽略的快变量及其边界条件。用奇异摄动方法求解飞行器制导非线性两点边值问题，可获得算法较简单，并可在弹上实时解算的近最优制导律［2-3］。

文献［4］针对超声速飞行器的最大航程滑行问题，将动力学方程分成三个层次，用奇异摄动方法求解了一种最大航程闭环导引律。文献［5］考虑了球形地球上的飞行器质点动力学模型，推导了奇异摄动最大航程制导律，给出了该算法与用序列二次规划(SQP)算法解算出的最优弹道和热流率曲线。无热流约束的弹道均为跳跃-滑翔式弹道，飞行中产生的热流率也较大。

针对上述问题，本文利用文献［6］中的高超声速飞行器的气动模型，用奇异摄动和动态逆方法为高超声速导弹推导了一种使热流率较低的最大末速中制导律。

1 导弹质点动力学模型

式中，r，h，E，γ，m，n 和 R0分别为航程、高度、比能、弹道倾角、质量、过载和地球平均半径。问题的初始条件为:

式中，CD0和CDt分别为零升阻力系数和升致阻力系数。动压定义为q=ρV2/2。各气动力系数见文献［4］。导弹迎角为:

式中，m，g，S分别为导弹的质量、当地重力加速度和参考面积，“～”表示变量的实际值。

令导弹飞行时产生的最大热流率为:

式中，热流率单位为W/cm2。

文献［6］用奇异摄动方法为高超声速飞行器推导了一种最远航程制导律，并用其与配点法和SQP方法解算出的最优弹道进行比较，证明了高超声速导弹的无约束弹道为跳跃-滑翔弹道。当导弹飞行至较高高度时，指令过载很小，甚至趋近于0。跳跃式弹道可很好地为导弹保存能量，但产生的热流率较大，不适于工程实际应用。

根据文献［7］中的结论，要减小热流率，就应使飞行弹道尽量平滑。用一些寻优方法，经过反复迭代运算可以得到较理想的结果，但其所需运算时间长，无法在飞行器上实时进行。另外，目标的运动，以及导弹在实际飞行中受到的各种干扰，均会导致飞行状态发生改变，从而无法满足跟踪最优值所需的条件。

2 奇异摄动中制导律

由于高超声速导弹飞行时间较长，需要在中制导段尽量保存能量，以保证末端拦截有足够的能量。问题变成使微分方程式(1)～式(4)所描述的系统从初始状态转移到预测拦截点在笛卡尔坐标系中的末端位置(rf，hf)，使得末端比能最大。假设目标以当前速度作匀速直线运动，则经过剩余飞行时间tgo后，其所处位置作为预测拦截点。剩余飞行时间估算如下:

式中，Rtm为导弹与目标的距离;Vc为接近速度;a为导弹沿视线方向的平均加速度，认为与导弹轴向加速度相等。

用文献［8］中介绍的方法估算各状态变量的时间常数。根据其大小可将变量分成:慢变量(r，E)、中间变量h和快变量γ。在中间变量和快变量前分别插入小参数 ε1(0＜ε1＜1)和 ε2(0＜ε2＜1)，可得到导弹的质心动力学奇异摄动模型为:

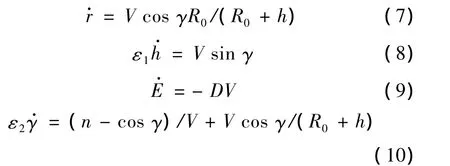
为使末端速度最大，可令性能指标为:J=－Ef。

2.1 降阶系统

最慢变量构成了降阶系统，由降阶系统求解出的解称为外解。令ε1=ε2=0，得到γ=0，n=1－V2/(R0+h)。带入式(7)～式(10)，得到降阶系统为:，其中:D=D0+K［1－V2/(R0+h)］2/q;高度h为零阶系统的控制量。Hamilton函数写成:H=λrVR0/(R0+h)－λEDV。由伴随方程，可知 λr为常数。由横截条件 λE(tf)= －1和H(tf)=0，得:

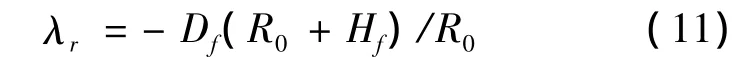
系统中各变量与时间无关，因此H(t)=0，可求得:

由控制方程∂H/∂h=0，带入式(11)和式(12)可得:

式(13)为h和E的隐函数。为加快弹上运算速度，可先将不同比能下的∂D/∂h与高度h的关系列成表格，这样通过插值即可求出与某指定能量下对应的最优高度h*。根据第1节中导弹气动力系数，计算出的比能与降阶最优高度关系如图1所示。

图1 降阶系统最优高度与比能的关系Fig.1 Relationship between reduced order optimal altitude and specific energy

本节中的V，D，h均为降阶值，下文中用上标“o”表示外解中的变量。降阶系统中忽略了高度变量的边界值。为使导弹能够达到预定位置，对降阶最优高度作如下修正:

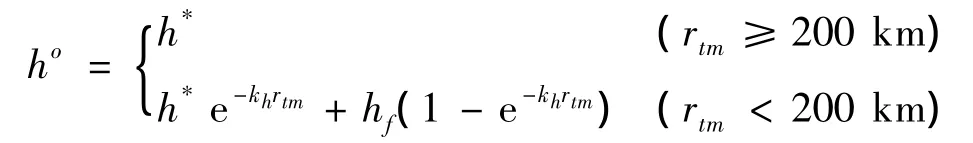
式中，kh为待选系数;rtm为两者之间的水平距离。

2.2 第一边界层

在飞行器质量不变和一定速度条件下，飞行器受到的零升阻力随海拔高度的增加而减小，由相同过载产生的阻力随海拔高度的增加而增加。因此，当指令过载不为0时，存在一个使阻力达到极小值的高度。

从物理上看，式(13)的意义在于:在某能量状态下，在降阶最优高度上作水平飞行时，飞行器受到的阻力最小。为得到一较平滑的弹道，边界层修正得到的系统控制量应使导弹能在降阶最优高度上飞行。

令 ε1=1，ε2=0，则 n=cos γ［1 － V2/(R0+h)］，得到的第一边界层动态由高度动力学方程决定。该层的控制量为弹道倾角γ。用动态逆方法对该层进行求解，第一边界层的系统方程和输出方程为:

该系统并非仿射非线性系统，因此将控制量改设为:

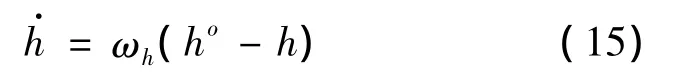
式中，ωh为待定系数。系统的控制为:

将式(14)带入，整理后可得到期望弹道倾角的表达式为:

对导弹系统的时间尺度分析可知，速度和高度变量在相同的时间尺度上，因此该层中的速度变量可看作当前导弹速度V。考察式(15)所示的一阶系统，其性能主要取决于h的时间常数。

下文中用上标“i1”表示第一边界层中的变量。该层计算中忽略了控制量弹道倾角的边界条件。为了使导弹在中制导末端，导引头能够顺利截获目标，需对最优进行修正:

其中:

2.3 第二边界层

令ε1=ε2=1，可得到第二边界层动力学方程，为系统方程完整形式。其控制变量为指令过载n。第二边界层系统动态主要由γ的动力学方程决定，控制量为n。其系统方程和输出方程为:

第二边界层系统为原系统中最快的一层，认为其中的变量均可取为当前值。可看出，上式所示系统是一个仿射非线性系统，可直接构造逆系统并求解控制律。求得控制量为:

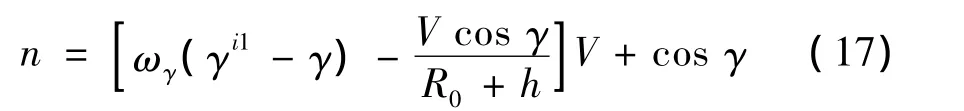
式中，ωγ为待定系数。

2.4 中制导算法

通过式(13)得到降阶最优后，用式(16)和式(17)即可计算得到导弹的指令过载。

根据动态逆理论，式(16)和式(17)中的待定系数ωh和ωγ应分别为高度变量和弹道倾角变量的时间常数的倒数。用文献［4］介绍的方法可估算变量的时间常数，但该方法依赖人工选取的典型值，因此估算出的时间常数在某区间内均可取值。文献［9］中介绍了如何根据二阶系统阶跃响应分析方法选取合适的时间常数值的方法，然而由于高超声速导弹飞行速度快，可达到很高的高度，导致其受到的阻力对指令过载的变化相当敏感。因此，当导弹处于很大的高度时，其指令过载趋近于0，这样才不会使飞行器能量迅速损失。

对于本文中的例子，导弹在初始一段时间内从较大的高度下落，需对初始下降段的降阶最优高度和第一边界层最优弹道倾角进行修正:当h=92 008 m时，将导弹以当前状态作自由下落的弹道高度作为降阶最优高度;将导弹以当前状态作自由下落的弹道倾角作为第一边界层最优弹道倾角，以保证导弹在最初下落段指令过载趋近于0。

3 仿真算例

本文用Matlab软件对制导律进行了仿真验证。导弹的初始状态为:r0=0 m，h0=112 080 m，V0=5164.9 m/s。设目标初始状态 ht(t0)=10 km，rt(t0)=5 500 km。目标以Ma=2的速度向导弹迎面匀速等高飞行。仿真过程中，令迎角α≤25°，导弹和目标的距离小于等于10 km时进入末制导，仿真结束。仿真结果见图2～图8。

图2为导弹和目标弹道，可见该制导律可将导弹导引至目标附近。

图2 导弹和目标弹道曲线Fig.2 Trajectories of missile and target curve

图3 和图4分别为高度和弹道倾角曲线。可以看出，基于动态逆的奇异摄动制导律的本质是使导弹跟随降阶的最优值。

图5为比能曲线。可以看出，在下落段，导弹能量几乎没有损失;在平稳飞行段，能量亦平稳减小，能够较好地为末端拦截保存能量。

图3 高度曲线Fig.3 Altitude curve

图4 弹道倾角曲线Fig.4 Flight path angle curve

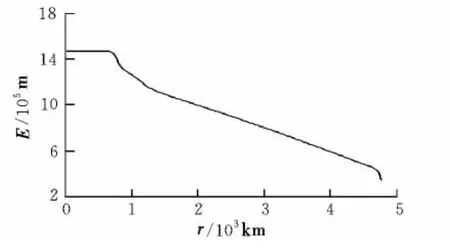
图5 比能曲线Fig.5 Specific energy curve

图6 为指令过载曲线。可以看出，在导弹下落的初始段，指令过载趋近于0，使该段能量损失减少到最小。

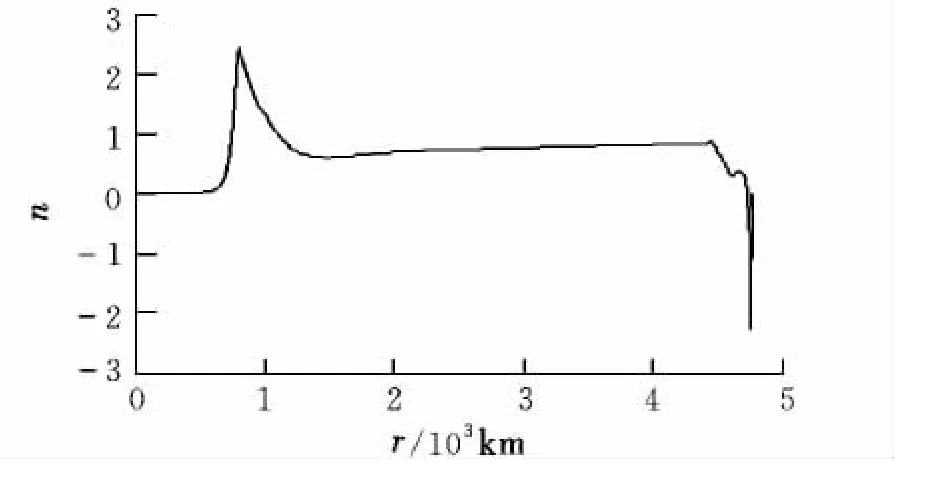
图6 指令过载曲线Fig.6 Command overload curve

仿真算例中，用迎角作为导弹的控制量。由图7所示的迎角曲线可看出，在短暂的自由下落结束后，迎角立即增大到最大值，以产生足够的过载使导弹高度调整至降阶最优高度位置。

图7 迎角曲线Fig.7 Angle of attack curve

导弹沿降阶最优高度飞行，形成了平滑的弹道，使大部分飞行时间内由图8所示的热流率曲线没有发生大的变化。在弹道末端，由于调整导弹飞行至目标附近，产生了较大的指令过载，热流率也有所上升。整个中制导段，最大热流率为551.02 W/cm2，大大低于跳跃-滑翔弹道的最大热流率值。通过调整动态逆控制器中的系数ωh和ωγ，可获得更小的最大热流率，以达到工程应用的要求。

图8 最大热流率曲线Fig.8 Maximum heating rate

4 结束语

本文针对高超声速导弹的无约束中制导弹道产生热流率过大的问题，用奇异摄动和动态逆方法推导了一种最大末速中制导律。用动态逆方法跟踪由降阶系统计算得出的最优高度和由第一边界层系统计算得出的最优弹道倾角，得到了一个闭环近最优中制导律。仿真结果可见，本文推导的中制导律除可将导弹导引至目标附近，并为末端拦截保存能量外，产生了占中制导绝大部分时间的平滑弹道，使热流率曲线在该段时间内没有突变，并且与无热流约束的最优滑行弹道相比，虽然保存能量能力稍弱，但大大减小了最大热流率，符合工程应用的要求。

［1］ 张丽静，刘东升，于存贵，等.高超声速飞行器［J］.航空兵器，2010，(2):13-16.

［2］ Naidu D S，Calise A.Singular perturbations and time scales in guidance，navigation and control of aerospace system［R］.AIAA-95-3321，1995.

［3］ Cheng V H L，Gupta N K.Advance midcourse guidance for air-to-air missile ［J］.Journal of Guidance，1986，9(2):135-142.

［4］ Sheu D L，Chen Y M，Chang Y J.Optimal glide for maximum range［R］.AIAA-98-4462，1998.

［5］ 乔清青，陈万春，李佳峰.高超声速飞行器最大航程滑行奇异摄动导引律［C］//临近空间飞行器及防御技术发展论坛文集.上海:中国航天科技集团公司第八研究院第八设计部，2010:119-127.

［6］ Morimoto H，Chuang C H.Minimum-fuel trajectory along entire flight profile for a hypersonic vehicle with constraint［R］.AIAA-98-4122，1998.

［7］ Yu Wenbin，Chen Wanchun.Guidance scheme for glide range maximization of a hypersonic vehicle［R］.AIAA-2011-6714，2011.

［8］ Ardema M D，Rajan N.Slow and fast state variables for three-dimensional flight dynamics［J］.Journal of Guidance，1985，8(4):532-535.

［9］ 乔清青，陈万春.基于动态逆的空空导弹奇异摄动中制导律［J］.北京航空航天大学学报，2011，37(11):1365-1371.