考虑高阶系统动力学滞后的最优制导律研究
陈欢,刘蛟龙,尉建利,于云峰
(1.西北工业大学航天学院,陕西西安710072;2.北京航天自动控制研究所系统理论与仿真技术研究室,北京100854)
0 引言
导弹制导精度是导弹武器系统的重要战术指标之一,提高导弹的制导精度不但可以有效地增强导弹攻击效率,而且可以减轻导弹重量、提高导弹机动能力和突防能力[1-2]。
在实际应用过程中,经典比例导引律和增强型比例导引律使用最为广泛。经典比例导引律没有考虑制导系统动力学滞后和目标机动的情况[3-4];增强型比例导引律考虑了目标机动情况,并对其进行了一定程度的有效补偿。目前,基于二次型性能指标的一阶最优制导律的研究已经非常成熟[5],不同于经典比例导引律,该制导律对目标的机动和导弹指令响应动力学滞后进行了一定程度的补偿[6],制导性能相对于比例导引律有了较大程度的提高。文献[4,6-7]分别从不同的角度给出了基于最优控制理论的一阶最优制导律推导过程,并通过仿真分析表明了其优越性。文献[3,5,8]已经考虑到了制导系统动力学阶数对制导精度的影响。文献[3]分析了制导系统动力学对制导系统的影响,并给出了相应的仿真结果;文献[5]重点对三阶和四阶制导系统最优制导律的形式、增益获取途径和仿真应用进行了理论研究。但总的来说,随着测量状态的增加和测量精度的提高,研究高阶最优制导律成为一种必然趋势[5]。
本文基于文献[2-3]中的典型五阶制导系统模型,提出了一种高阶最优制导律,并给出了详细的推导过程。通过与增强型比例导引律和一阶最优制导律进行比较,表明了所提出的制导律的优越性。
1 模型的建立
1.1 弹-目之间简化二维数学模型的建立
图1为导弹与目标之间的二维线性化运动模型。在该简化模型中,x为视线的基准方向;MT表示目标瞄准线;M为拦截导弹,T为目标,二者的速度分别为VM和VT,加速度分别为nL和nT。
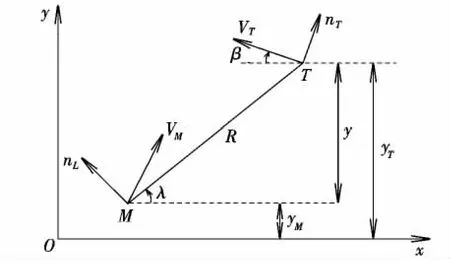
图1 弹-目简化二维数学模型Fig.1 Two-dimensional missile-target engagement geometry
导弹与目标之间的相对加速度可以表示为:
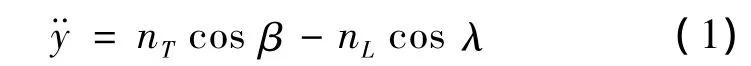
一般β和λ都很小,因此上式可以近似为:

同样,利用小角度假设,导弹与目标之间的相对距离y可以近似表示为:

在线性分析中,假设接近速度VC为常值,因此有:
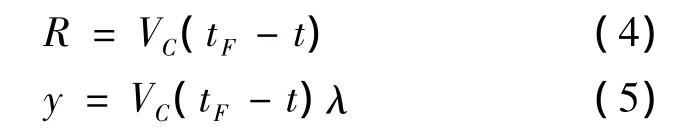
式中,R为导弹与目标之间的相对距离;λ为目标视线角;tF为末制导时间。式(2)和式(5)组成了导弹与目标的相对运动方程。
1.2 考虑动力学滞后的制导系统模型的建立
本文介绍的最优制导律为基于考虑五阶动力学滞后的制导系统。根据文献[2-3]中的介绍,此处将导引头、噪声滤波器等效为二阶动力学环节。将飞控系统等效为典型的三阶动力学滞后环节,即:
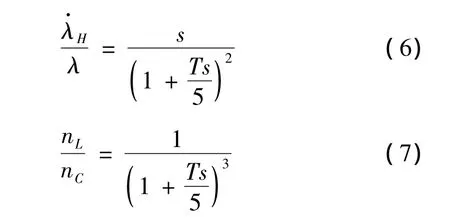
式中,nC为指令加速度;T为等效弹体时间常数。由以上数学模型,可得相应的导弹与目标制导系统数学模型结构图,如图2所示。
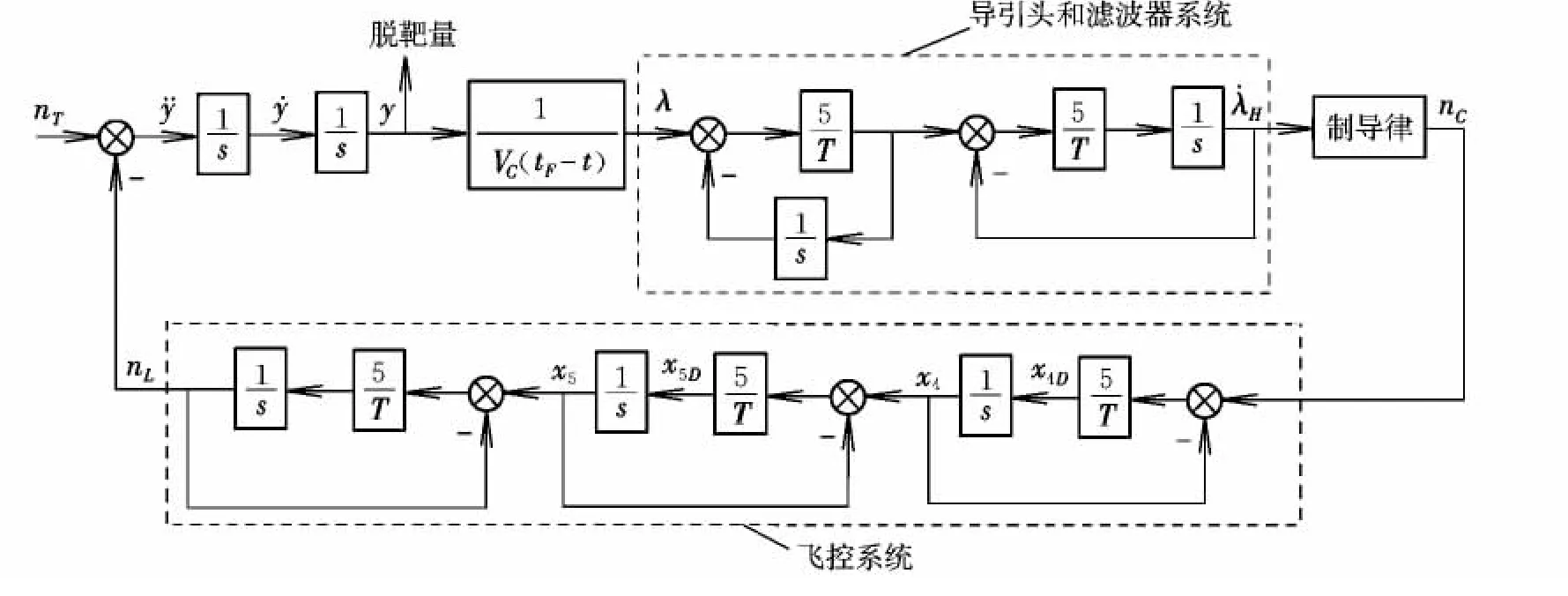
图2 考虑五阶动力学滞后的制导系统结构图Fig.2 Fifth-order binomial guidance system
2 五阶最优制导律理论推导
2.1 最优制导律推导过程
制导系统模型如图2所示,系统状态方程可表示为:

即:


式中,F为系统状态矩阵;G为输入控制矩阵。该状态空间向量方程在末制导时刻的解为:
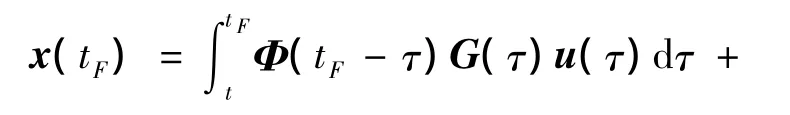

根据式(10)可得到表征导弹与目标碰撞时刻脱靶量y(tF)的表达式,简化表述如下:
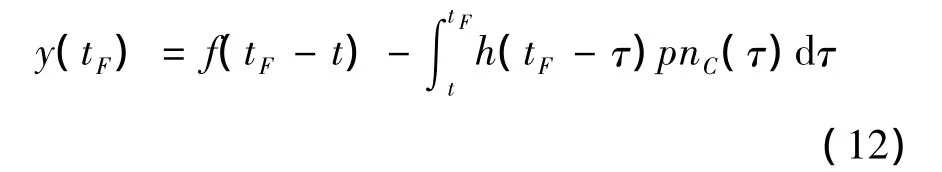
考虑到现代反导战争中目标的大机动飞行对导弹的需用过载要求不断提高,高精度制导对导弹脱靶量也有很高的要求,设计制导律的首要考虑就是实现脱靶量为零,其次就是使用最少的燃料来实现第一个要求。
对于大气层外飞行的导弹,通过侧向发动机来实现导弹的机动运动,此时导弹需要充足的燃料来实现机动,进而控制导弹实现大气层外的高精度拦截。通常情况下,用侧向转移速度ΔV来衡量导弹机动过程所需燃料的多少,ΔV又可进一步转化为指令加速度:

由此可见,对达到零脱靶量使用燃料最少的限制,可归结为对拦截弹需用过载的限制。由于积分在数学运算上比较复杂,一般情况下选取对nC的平方进行积分来代替直接求取ΔV。综上,本文选取以 达到最小为约束条件来实现零脱靶量,即受限于最小的
当y(tF)=0时,由式(12)得:

由Schwartz不等式可得:
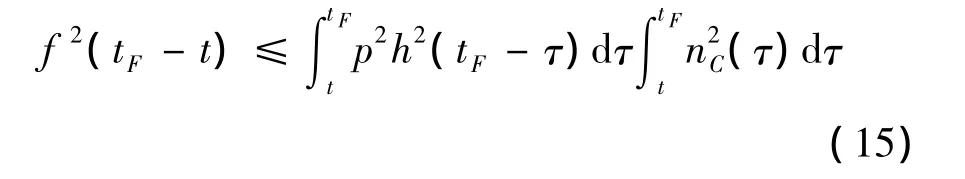
即:
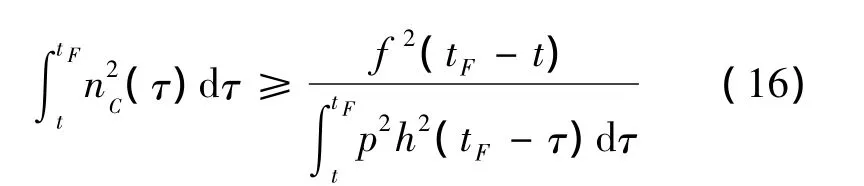
根据Schwartz不等式的性质知,当且仅当nC(t)=kph2(t-t)时,等号成立,即取最小值。此
F时下式成立:

令x=tgo=tF-t,tgo表示剩余飞行时间。易求得:
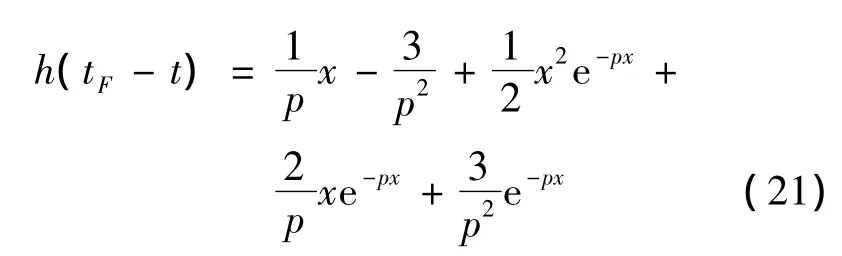
将式(19)~式(21)带入式(18),即可得到考虑动力学滞后的最优制导律为:
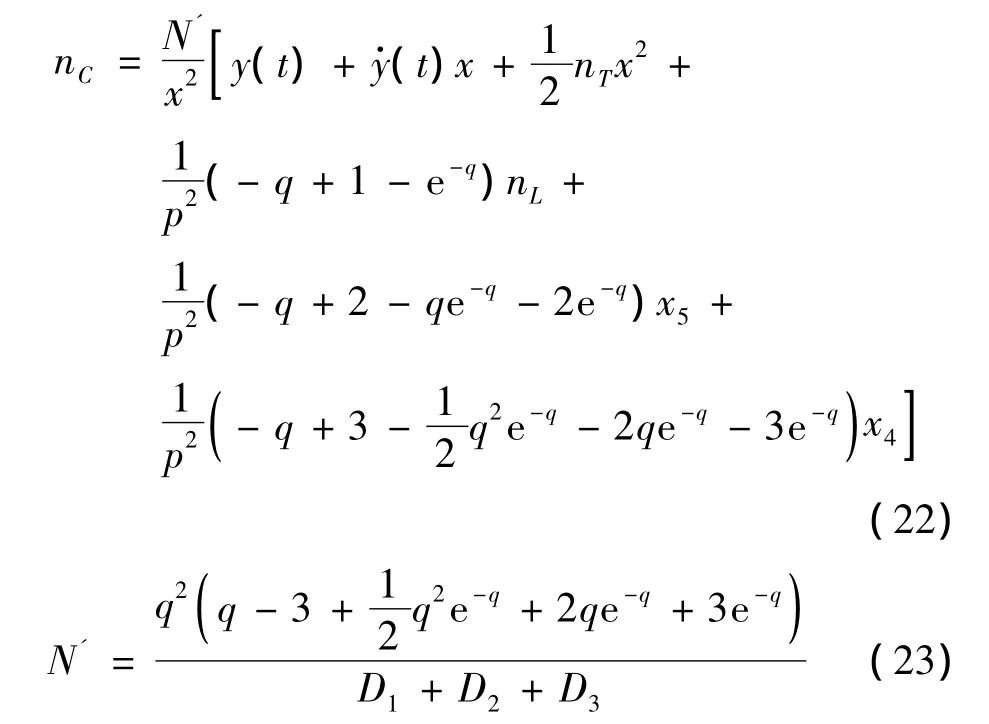
2.2 最优制导律简化分析
根据式(22)和式(23)可知,如果只考虑一阶动力学滞后环节,即 x4=x5=0,且,此时五阶最优制导律可简化为考虑一阶动力学环节的最优制导律,即:
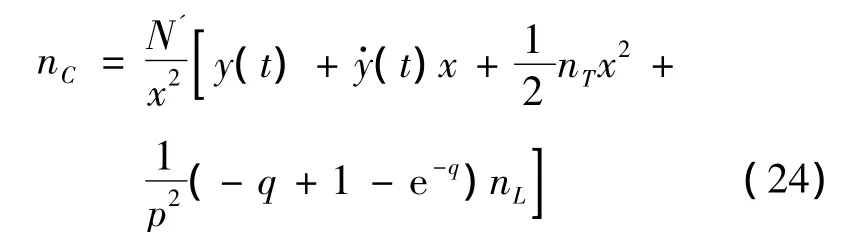
如果不考虑高阶系统动力学滞后,认为制导系统动力学响应速率可以无限快,即视等效弹体时间常数T无限趋近于零,那么有q→∞。此时,由式(22)和式(23)可得 N'→3,且

由此可见,考虑高阶系统动力学滞后环节得到的最优制导律式(22)退化为不考虑动力学滞后的经典的增强型比例导引律。此时如果目标不进行任何形式的机动,最优制导律就是有效导航比为3的经典比例导引律。
2.3 剩余飞行时间估算改进
末制导过程中剩余飞行时间估计误差较大,会导致制导精度严重降低,甚至会造成导弹脱靶。文献[9-10]中给出一种常见的补偿后剩余飞行时间的方法。由式(23)可知,剩余飞行时间直接影响到有效导航比N',本文越过对剩余飞行时间的补偿而直接补偿有效导航比N',通过反复验证,得到不同补偿值情况下脱靶量y(tF)的大小,如表1所示。
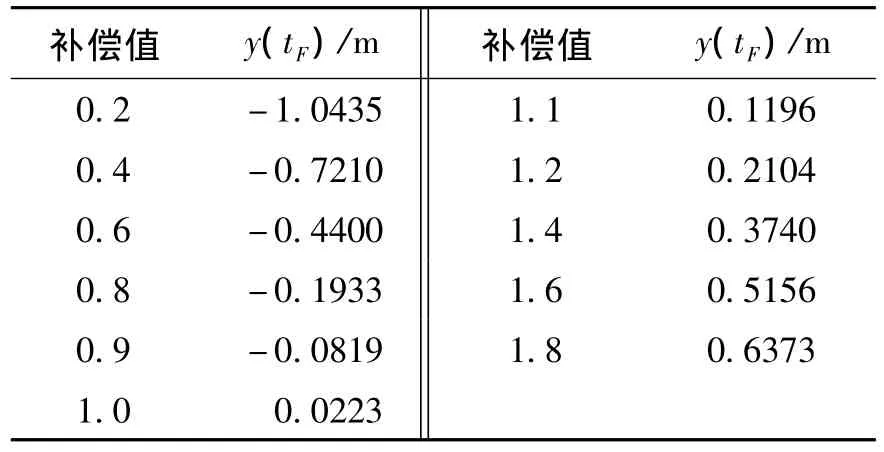
表1 不同补偿值情况下脱靶量的大小Table 1 Miss distance of different compensation cases
根据表1,为实现高精度制导,取N^'=N'+1,N^'为补偿后的有效导航比。
3 仿真结果及分析
本文仿真过程中考虑了对拦截弹过载能力的限制,在图2的基础上对基本制导回路引入过载饱和使之变成非线性制导系统。
仿真初始条件:末制导飞行时间tF=10 s,弹目接近速度VC=1 220 m/s,等效弹体时间常数T=1 s,目标机动过载nT=6,最大可用过载nCmax=6,9。
图3~图8分别为增强型比例导引律(APN)和一阶最优制导律(OPG1)在最大可用过载nCmax分别为6和9时与五阶最优制导律(OPG5)关于脱靶量和侧向转移速度的对比曲线。图中,APN取有效导航比N'=4。
图3和图4为nCmax=6,当导弹机动能力与目标机动过载相等时,一旦考虑制导系统动力学特性,无论是APN和OPG都会导致拦截弹不同程度脱靶,这意味着要想实现直接碰撞需要拦截弹具备高于目标的机动能力。
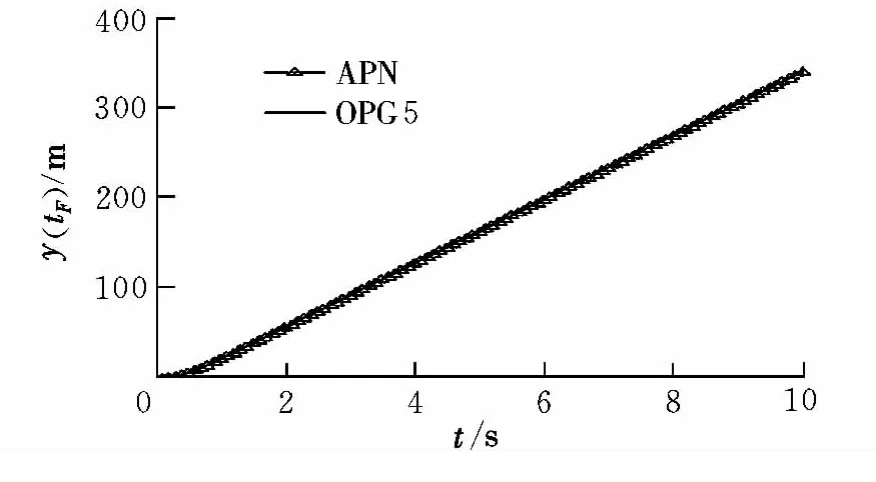
图3 APN与OPG5脱靶量对比Fig.3 Miss comparison for APN and OPG5
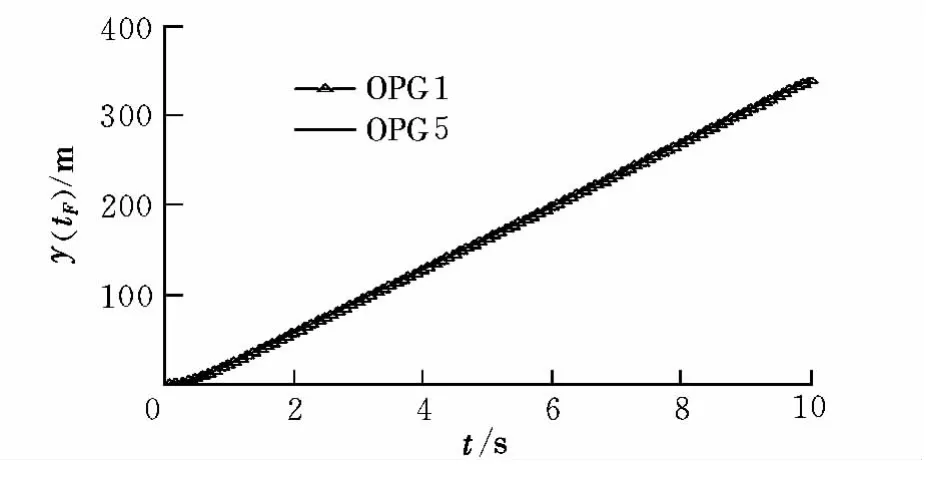
图4 OPG1与OPG5脱靶量对比Fig.4 Miss comparison for OPG1 and OPG5
图5 和图6为nCmax=9时APN和OPG1与OPG5脱靶量的对比曲线。可以看出,APN在不考虑动力学特性情况下可以很快实现脱靶量为零;当考虑动力学特性后,随着模型的细化,APN制导精度逐渐降低。OPG1应用于一阶滞后系统制导精度较高,而应用于本文的五阶动力学系统后几乎不能实现对目标直接撞击。本文所介绍的OPG5虽然在末制导时间较短时脱靶量较大,但是当7 s后可以实现零脱靶量的目标,制导精度明显高于APN和OPG1。
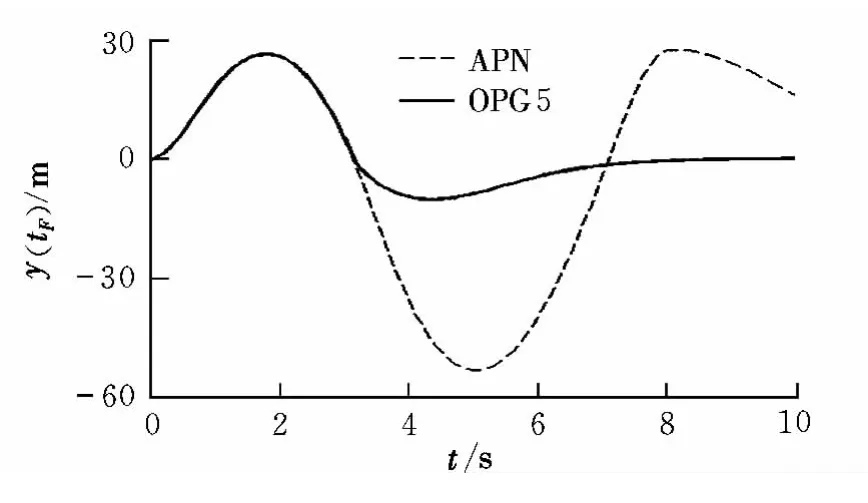
图5 APN与OPG5脱靶量对比Fig.5 Miss comparison for APN and OPG5
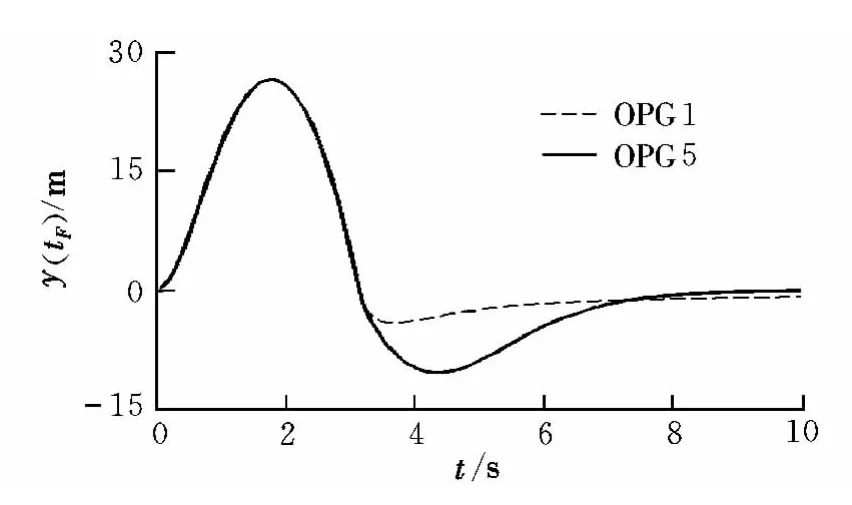
图6 OPG1与OPG5脱靶量对比Fig.6 Miss comparison for OPG1 and OPG5
图7 和图8为nCmax=9时采用APN与OPG5导弹实现拦截所需侧向转移速度ΔV的大小。可以看出,在考虑制导系统动力学特性后,本文所述制导律OPG5能以较低的侧向转移速度实现对目标的精确撞击。
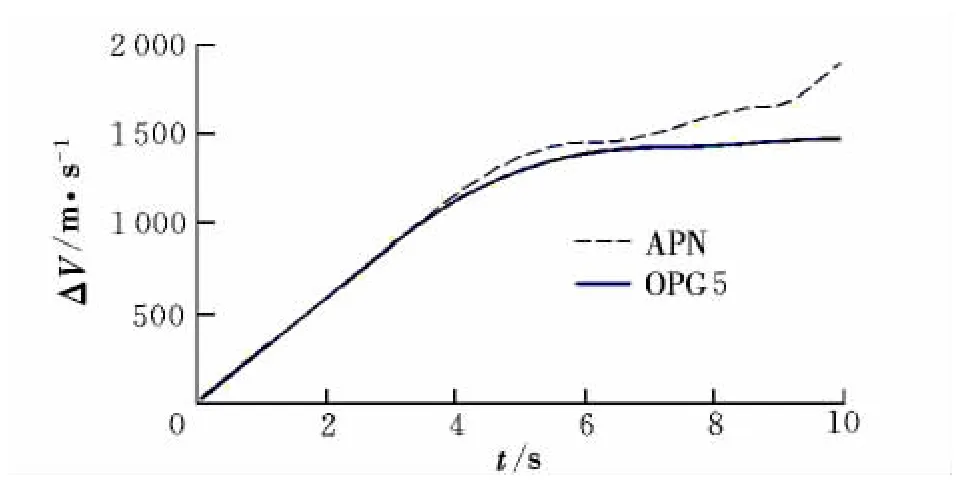
图7 APN与OPG5侧向转移速度对比Fig.7 Lateral divert comparison for APN and OPG5
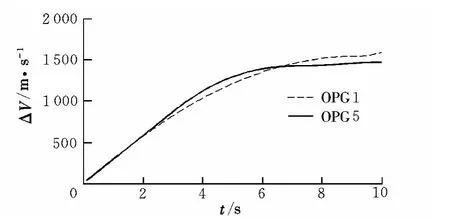
图8 OPG1与OPG5侧向转移速度对比Fig.8 Lateral divert comparison for OPG1 and OPG5
4 结束语
本文根据最优控制理论,给出了考虑五阶动力学滞后环节的最优制导律详细的推导过程。并与增强型比例导引律和一阶最优制导律进行了比较,给出了三种制导律在目标常值机动情况下脱靶量和侧向转移速度曲线。五阶最优制导律有效地降低了制导系统动力学特性对脱靶量的影响,同时,减小了拦截弹对侧向转移速度的需求。当导弹过载能力受到限制时,五阶最优制导律能在较短的末制导飞行时间内实现零脱靶量的要求。但是,本文所介绍的五阶最优制导律在工程使用上还有待进一步验证,如何获取精确的目标机动过载信息以及怎样精确计算剩余飞行时间,仍需进行深入研究。
[1] 王洪强,邵晓巍,周刚,等.一种改进的组合末制导律研究[J].计算机技术与发展,2011,21(12):239-242.
[2] Zarchan P.Tactical and strategic missile guidance[M].Washington D C:AIAA,Inc,2007:149-152.
[3] 张宏,夏群力,祁载康,等.基于目标机动补偿的增强型比例导引性能研究[J].红外与激光工程,2007,36(S1):82-87.
[4] 李遗,宋振铎,刘德忠.应用极小值原理推导一阶动力学最优制导律[J].弹箭与制导学报,2008,28(5):83-85.
[5] 刘德忠,祁载康.基于二次型性能指标的高阶最优制导律研究[C]//飞行力学与飞行试验2006学术交流年会论文集.西安:飞行力学杂志社,2006:292-297.
[6] 许涛,杨军,展建超.红外制导导弹最优导引律工程实现方法研究[J].计算机仿真,2010,27(2):96-100.
[7] 王辉,林德福,程振轩.考虑动力学滞后的最优比例导引律[J].弹箭与制导学报,2011,31(4):33-36.
[8] 姜玉宪.脱靶量估算和广义比例导引[J].宇航学报,1994,15(1):8-13.
[9] 肖增博,雷虎民,马附洲.一种最优末制导律研究[J].现代防御技术,2009,37(2):18-21.
[10]徐琰珂,梁晓庚.对剩余飞行时间估计误差不敏感的末制导改进方法[J].火力与指挥控制,2011,36(10):100-103.

