柱面螺线的一般方程*
张巧媚,纪永强
(湖州师范学院 理学院,浙江 湖州313000)
0 引 言
设C:r=r(s)是空间挠曲线,s是曲线C的弧长,在文献[1]中有如下定义:若曲线C上每一点的单位切矢量e1(s)与定幺矢量δ成定角θ,即

则称曲线C是柱面螺线.由文献[1]有:
定理1[1]空间挠曲线C:r=r(s)是柱面螺线的充要条件是:曲线C上每一点的曲率k(s)与挠率τ(s)之比是非零常数a,即.
由文献[2]得下面定理成立.
定理2[2]设曲线C:r=r(s)是柱面螺线,S:ρ(s,v)=r(s)+ve2(s)是曲线C的主法线曲面,e2(s)是曲线C的单位主法矢量,C1:ρ1(s)=r(s)+e2(s)是曲线C的曲率中心轨迹.
(1)若C1是曲面S上的一条渐近线,则柱面螺线C是圆柱螺线.
(2)若C1是曲面S上的一条测地线,则柱面螺线C的一般方程是:

设C:r=r(s)是柱面螺线,曲线C的副法线曲面S的方程是:

其中:e3(s)是曲线C的单位副法矢量.曲线C的挠率中心轨迹C1的方程是:

显然,曲线C1在曲面S上.当C1是曲面S上的一条渐近线或C1是曲面S上的一条测地线时,可得柱面螺线C的具体方程.
由文献[1]可知,空间挠曲线C的基本公式是:
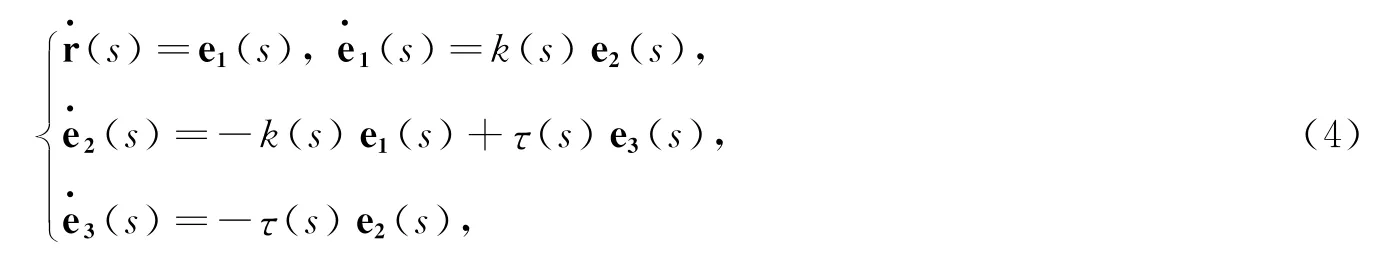
设s1是曲线C1的弧长,对(3)式关于s求导得:
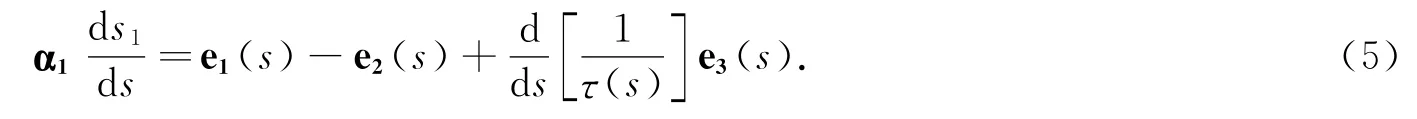
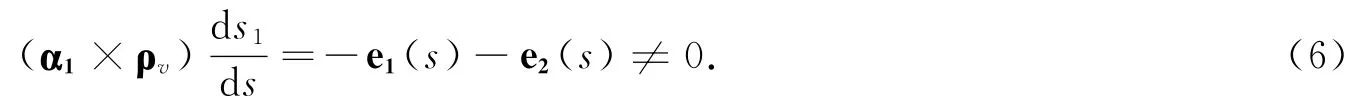
(6)式表明,沿曲线C1,曲面S的切矢量ρv与曲线C1的单位切矢量α1线性无关.因此,沿曲线C1,曲面S的单位法矢量是:

其中:ε=±1.对(5)式两边关于s求导,并由(4)式得:
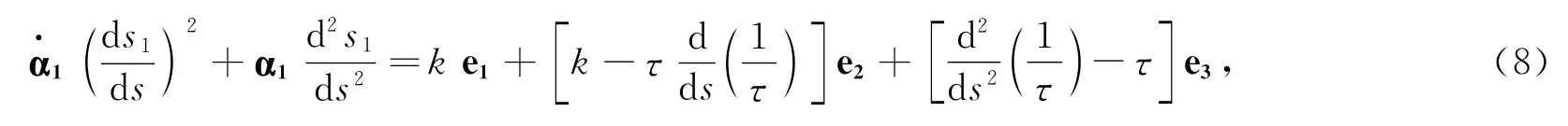
另外,在文献[3]给出了柱面螺线的一般方程:
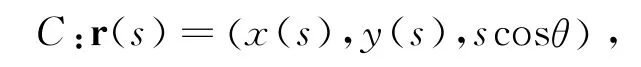
其中:θ为定角;x(s)和y(s)是任意函数.
事实上,x(s)和y(s)是满足某个条件的函数,不是任意函数.反例:曲线C:r(s)=不是柱面螺线.
下面给出x(s)和y(s)满足具体的条件,使得曲线为柱面螺线.
1 定理及其证明
定理1 设C:r=r(s)是柱面螺线,若曲线C的挠率中心轨迹C1是曲线C的副法线曲面S上的一条渐近线,则柱面螺线C的一般方程是:
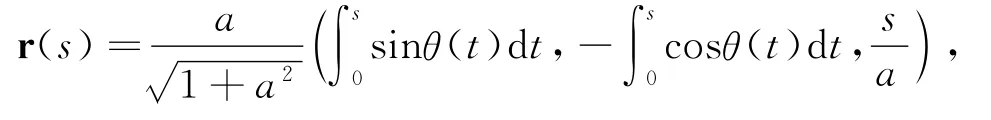
其中:
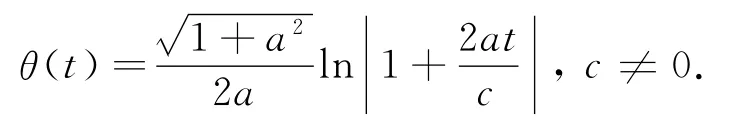
证明 由(6)式可知,曲面S的法矢量n(s)与曲线C1的单位切矢量α1正交,即它们的内积为零,即

由(7)式得:

在(8)式两边与n(s)作内积得:
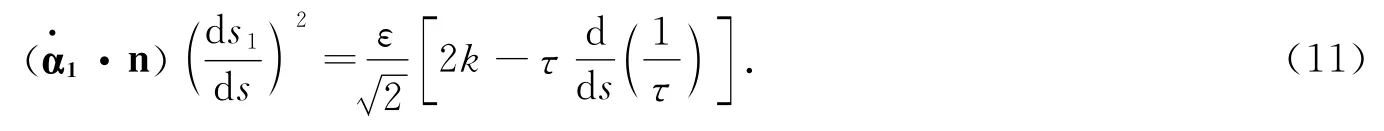
由文献[1]知,法曲率kn的定义是:

所以(11)式为:

由此可得,曲线C1是曲面S上的渐近线的充要条件是:沿曲线C1,法曲率kn≡0,由(13)式得:


由文献[4]得柱面螺线C的方程是:
其中:

定理2 设C:r=r(s)是柱面螺线,=a≠0.若曲线C的挠率中心轨迹C1是曲线C的副法线曲面S上的一条测地线,则柱面螺线C的一般方程是:
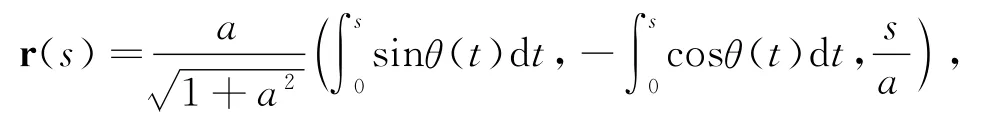
证明 将(5)式两边与曲面的法矢量n作外积,并由(7)式得:
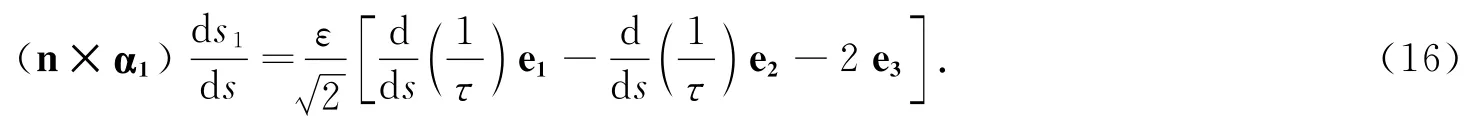
由(8)式两边与(n×α1)作内积得:
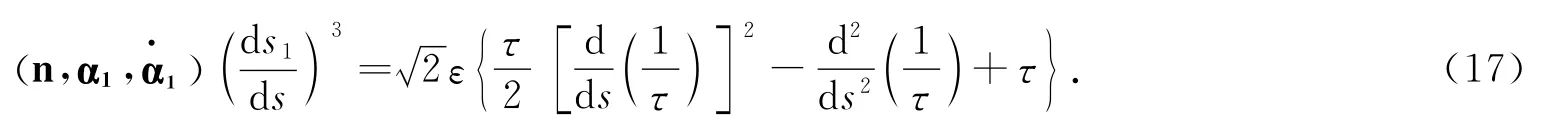
由文献[1]中测地曲率kg的定义知,kg=n,α1,( ),所以(17)式为:
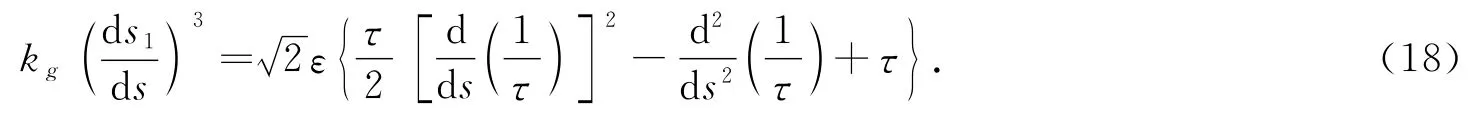
由此可得,曲线C1是曲线C的副法线曲面S上的测地线的充要条件是:沿曲线C1,测地曲率kg≡0.由(18)式得:
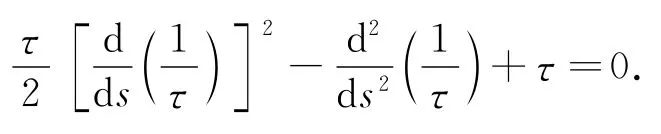
因为τ≠0,令t=,得:

(19)式两边关于s求导得,解得:

将(20)式代入(19)式得:
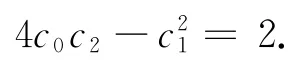
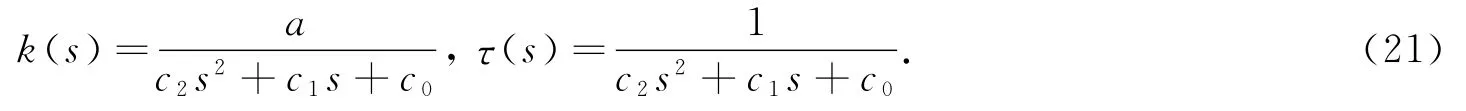
由文献[4]得柱面螺线C的方程是:
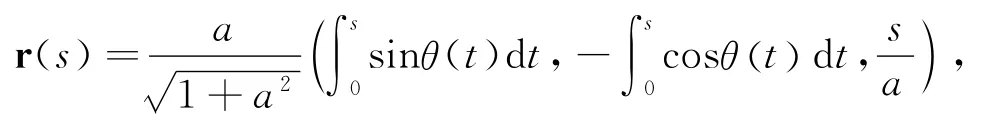
其中:
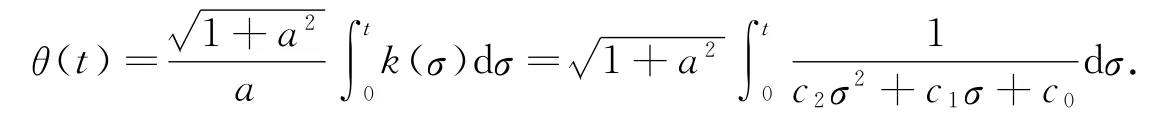
定理3 设C:r(s)=(x(s),y(s),z(s))是柱面螺线,δ=(0,0,1)为定幺矢量,则柱面螺线C的一般方程是:

其中:θ为定角;x(s)和y(s)是满足方程

的任意函数.
证明 曲线C的单位切矢量是:

又δ=(0,0,1),因为曲线C是柱面螺线,由(1)式得:
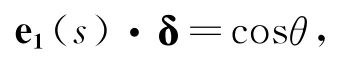
即(s)=cosθ,其中θ为定角,所以z(s)=scosθ.
又因为e1(s)是曲线C的单位切矢量,所以(s)2+(s)2+(s)2=1.由此可得:
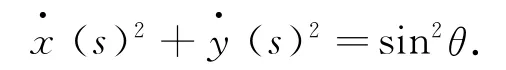
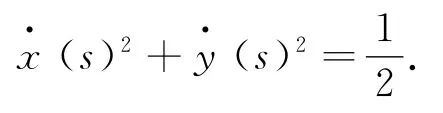
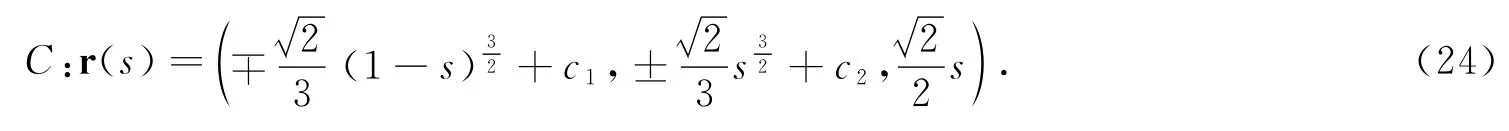
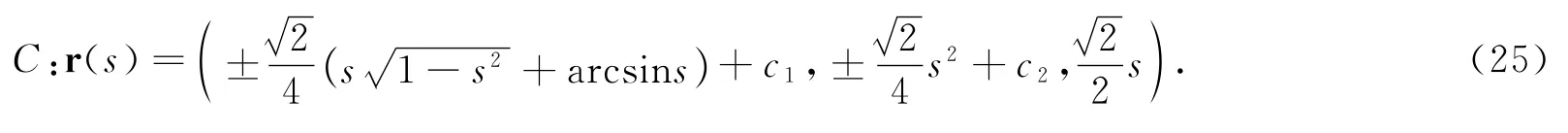
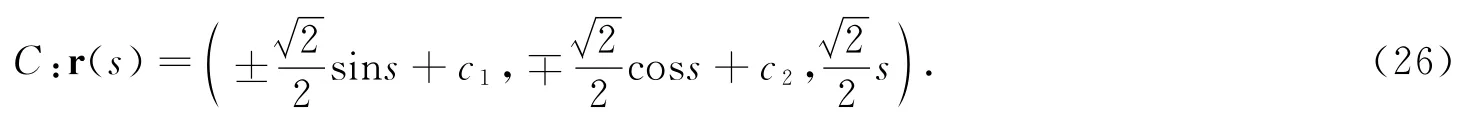
方程(26)式表示的柱面螺线是圆柱螺线.
[1]纪永强.微分几何[M].北京:高等教育出版社,2009.
[2]张量.两种特殊的螺旋线[J].数学的实践与认识,2011,41(12):187-190.
[3]梅向明,黄敬之.微分几何[M].北京:高等教育出版社,1988.
[4]沈纯理,黄宣国.微分几何[M].北京:经济科学出版社,1997.

