PUREX流程萃取体系下相关组分的分配比模型Ⅰ.U（Ⅳ）分配比模型

陈延鑫，何 辉，彭 力，高 巍，朱礼洋，李 斌，唐洪彬，王立京

1.中国原子能科学研究院 放射化学研究所，北京 102413；2.中国原子能科学研究院 劳动人事教育处，北京 102413

硝酸、铀、钚、镎、锝等元素是乏燃料溶解液中的主要成分，以上各元素的分配比模型是开展Purex流程计算机模拟研究的基础［1］。国内已开发了HNO3、U（Ⅵ）、Pu（Ⅳ）和Pu（Ⅲ）共4种组分的分配比模型，模型已在模拟程序中得到应用，其可靠性也在实验中得到了验证［2-3］。但是除这4种组分外，仍缺乏U（Ⅳ）、Np（Ⅳ）、Np（Ⅴ）、Np（Ⅵ）、Tc、Zr等组分的分配比模型或因已发表的分配比模型适用性较差而无法使用，因此在Purex流程计算机模拟程序中无法模拟以上组分的萃取行为及走向，有必要开展以上各组分的分配比模型研究。

U4＋与间的标准氧化还原电位为-0.32V，即使在空气中，U（Ⅳ）也会被O2缓慢地氧化，因此，在后处理流程中，以N2H4HNO3稳定的U4＋溶液通常作为还原剂用于铀钚分离工艺段（1B）。为了能够了解U（Ⅳ）在不同条件下的分配情况，国内外研究者［4-6］开展了大量的U（Ⅳ）分配比测量研究工作，并在此基础上，得到了一系列的U（Ⅳ）分配比模型［7-10］。与得到认可的HNO3、U（Ⅵ）、Pu（Ⅳ）和Pu（Ⅲ）的分配比模型不同，目前U（Ⅳ）分配比模型可靠性存在争议，如印度Kumar等［8］利用部分数据对Geldard等［7］的模型进行了验证，验证结果认为该模型的标准偏差能够达到300%。

因此，为了得到可靠的U（Ⅳ）分配比模型，本工作拟利用文献报道的U（Ⅳ）分配比数据对目前存在的U（Ⅳ）分配比模型进行验证，同时对模型展开必要的修正和验证工作。

1 分配比模型及计算方法

在Purex流程萃取体系下，金属元素及HNO3等组分的萃取反应可通过（1）式表述为：

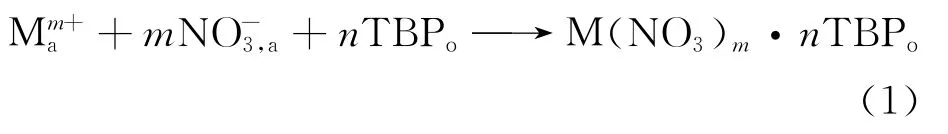
一般Mm＋会形成M（NO3）m·nTBP络合物被萃入TBP中，反应的热力学平衡常数K为：

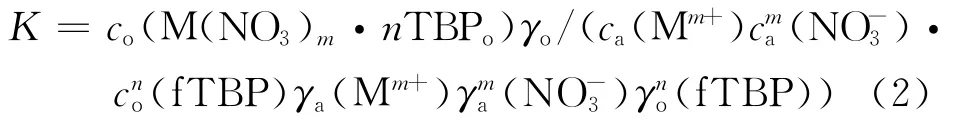
根据分配比定义：

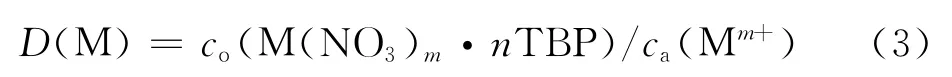
根据公式（2）和（3）可知，能够影响分配比的因素如式（4）所示：

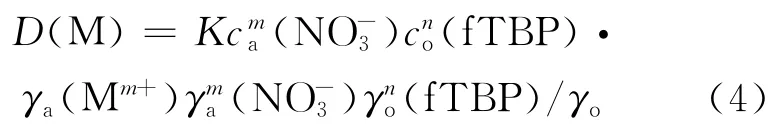
式中：c为摩尔浓度，mol／L；γ为活度系数；fTBP表示自由TBP；下角标a、o分别表示水相、有机相。因此，Purex流程中任一组分的分配比都与萃取平衡常数K、总硝酸根浓度、自由TBP浓度以及相应的活度系数相关。

各组分的活度系数随着体系中硝酸浓度或金属离子Mm＋浓度的改变而改变。各组分在水相、尤其是有机相中的活度系数数据匮乏，很难直接通过活度系数及萃取平衡常数建立起各组分分配比模型函数。为了解决这一问题，Richardson等［3］引入了表观平衡常数K＊，将表观平衡常数K＊拟合成总硝酸根浓度及温度的函数，形如式（5）所示：

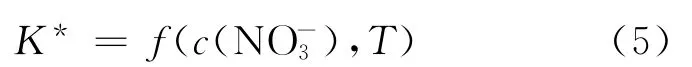
从而Purex流程中各组分分配比D（M）可用式（6）表示为：

式（6）中c（fTBP）表示平衡有机相中自由TBP浓度。

Richardson［3］、何 辉［2］等的研究已经得到了硝酸、U（Ⅵ）、Pu（Ⅳ）、Pu（Ⅲ）共四种组分的表观平衡常数表达式，具体参见文献［2］。在TBP-煤油／硝酸萃取体系中，U（Ⅳ）的萃取反应为：

则根据式（6），U（Ⅳ）的分配比为：

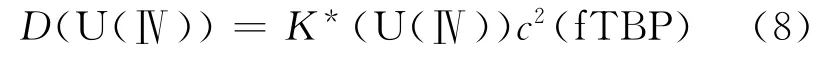
在Purex流程萃取体系下，U（Ⅳ）存在时，必然同时存在硝酸、U（Ⅵ）、Pu（Ⅲ）等组分，其他组分浓度的变化，必定会影响U（Ⅳ）的表观平衡常数，因此，根据Richardson分配比模型的拟合方法，将U（Ⅳ）的表观平衡常数K＊（U（Ⅳ））与总硝酸根浓度关联成形如式（9）的函数：

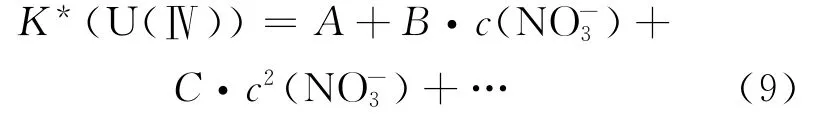
根据萃取平衡时的物料衡算，可以计算Purex流程萃取体系下U（Ⅳ）达萃取平衡时自由TBP的浓度c（fTBP）。对于待萃溶液中含有硝酸、U（Ⅵ）、U（Ⅳ）、Pu（Ⅳ）、Pu（Ⅲ）、肼的萃取体系萃取平衡时的c（fTBP）衡算公式为：

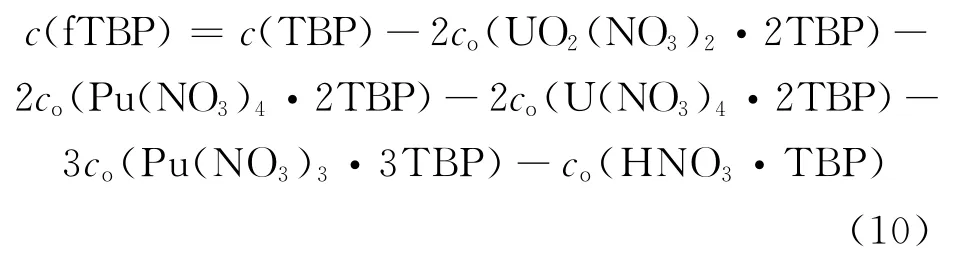
根据公式（6）中各组分对应的分配比代入公式（10），可以得到c（fTBP）与平衡水相中各萃取组分浓度间的关系，如公式（11）：

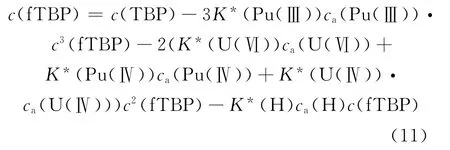
对于不同体积分数（φ，%）的TBP-煤油来说，TBP摩尔浓度为φ×3.651，从而对于30%TBP-煤油来说，总TBP摩尔浓度为1.095 3mol／L。由于Pu（Ⅲ）的分配比值极低，萃取平衡后，有机相中Pu（Ⅲ）结合的TBP很少，因此，可省略公式（11）中的三次方项，从而公式（11）简化为：

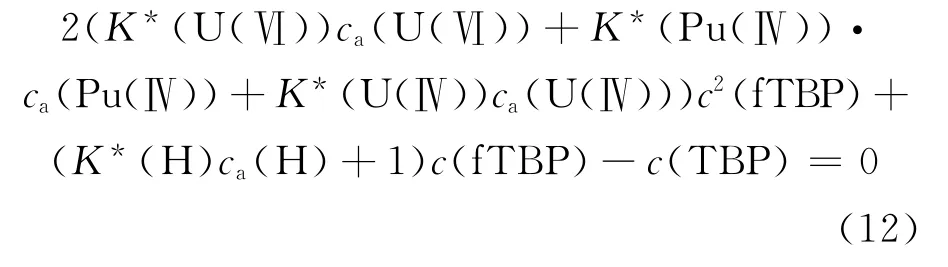
通过平衡水相中各组分的浓度可计算得到总硝酸根浓度和表观平衡常数，利用公式（12）可计算得到自由TBP浓度c（fTBP）的值，从而利用公式（6）可分别计算得到各组分的分配比值。

2 现有分配比模型及验证方法

2.1 现有分配比模型

美国Geldard等［7］以Richardson模型为基础，将25℃的U（Ⅳ）与35℃的Pu（Ⅲ）的分配比数据通过总硝酸根离子强度进行拟合，得到了U（Ⅳ）和Pu（Ⅲ）的分配比模型函数。通过该研究认为，当溶液中存在U（Ⅵ）时，U（Ⅳ）对离子强度的贡献减弱，可通过δ函数得到离子强度与各离子浓度间的关系为）＝c（H＋）＋2c（U（Ⅵ））＋（4-3δ）c（U（Ⅳ）），当U（Ⅵ）共存时，δ＝1，其他情况则为0。U（Ⅳ）的表观平衡常数为K＊（U（Ⅳ））＝K＊（U（Ⅵ））（0.054 1＋0.000 658c2，分配比计算模型为D（U（Ⅳ））＝K＊（U（Ⅳ））c2（fTBP），该函数计算结果的标准偏差为0.275 5。印 度Kumar等［8］利 用 部 分 数 据 对Geldard等的模型进行了验证，验证结果认为该模型的标准偏差能够达到300%。因此，他们利用文献数据对U（Ⅳ）的分配比数据开展进一步的拟合，得到D（U（Ⅳ））＝0.360 2c1.3615）c2（fTBP），标准偏差为0.270 9。日本Revised-MIXSET程序［8］中采用的U（Ⅳ）分配比模型为D（U（Ⅳ））＝exp（-3.336＋c1.9331））·c2（fTBP），文献中并未对该分配比模型的计算偏差进行报道，但是2008年日本的PARC程序［9］在模拟U（Ⅳ）的分配时，使用了该模型。综合以上分析，目前已发表的U（Ⅳ）模型汇总列于表1。

表1 已发表的U（Ⅳ）分配比模型Table 1 Three published U（Ⅳ）distribution models

2.2 验证方法

在Matlab2012软件平台上，利用文献报道的各分配比模型函数编写M文件，通过查找文献得到的分配比数据对各分配比模型进行验证并进行修正。

3 结果与讨论

3.1 现有模型验证及对比

文献［4-6］报道25℃下、U（Ⅳ）的分配比数据共计610组，其中U（NO3）4／HNO3-N2H5NO3／30%TBP-OK萃取体系下的数据253组，UO2（NO3）2-U（NO3）4／HNO3-N2H5NO3／30%TBP-OK萃 取体系下的数据357组。数据涵盖浓度范围为：平衡水相硝酸浓度为0.4～4.0mol／L，U（Ⅳ）质量浓度为5～50g／L，U（Ⅵ）质量浓度为15～150g／L，肼浓度为7×10-4～2mol／L。在Matlab软件平台上，分别对以上3种模型编写程序进行验证，验证结果示于图1和图2。

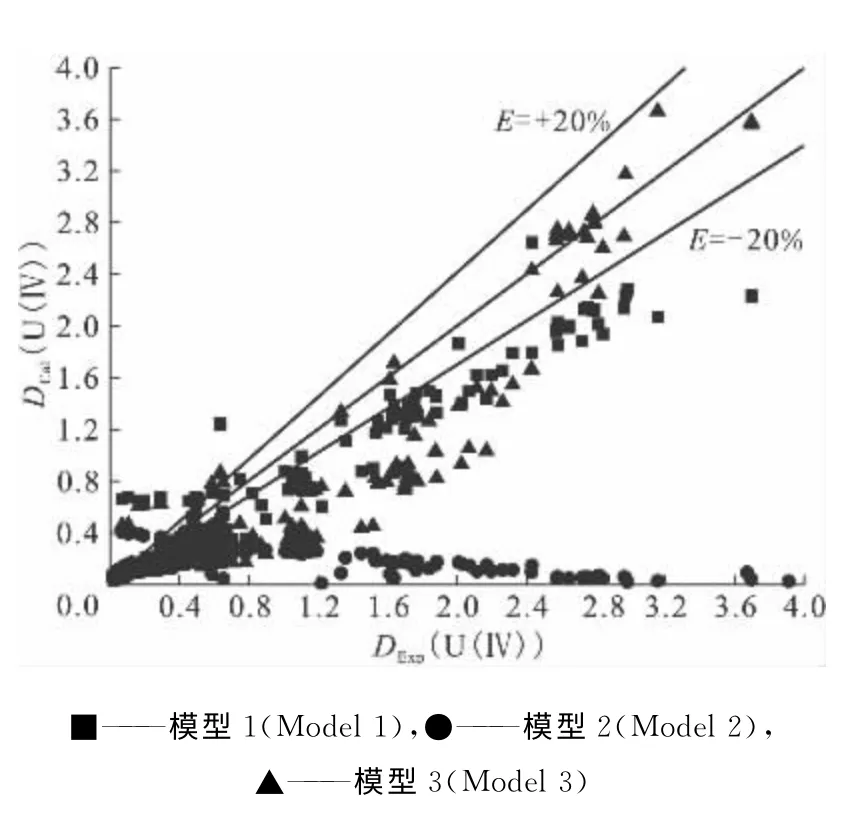
图1 U（NO3）4／HNO3-N2H5NO3／30%TBP-OK萃取体系下U（Ⅳ）分配比计算值DCal（U（Ⅳ））与文献实验值DExp（U（Ⅳ））对比Fig.1 A comparison of three models by plotting calculated DCal（U（Ⅳ））against experimentally obtained DExp（U（Ⅳ））in U（NO3）4／HNO3-N2H5NO3／30%TBP-OK system

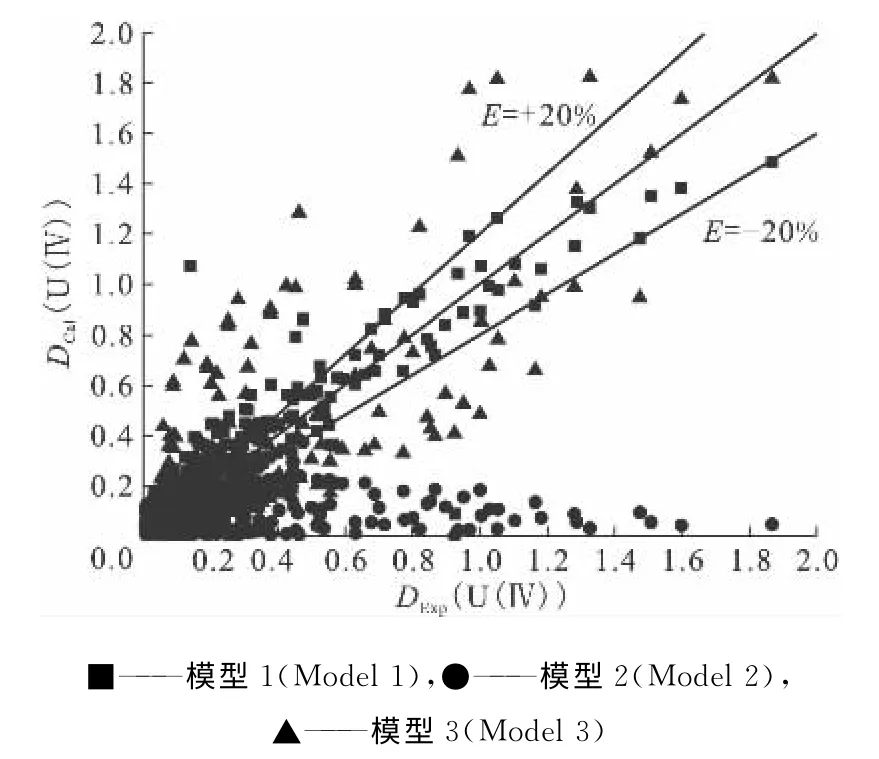
图2 UO2（NO3）2-U（NO3）4／HNO3-N2H5NO3／30%TBPOK萃取体系下U（Ⅳ）分配比计算值DCal（U（Ⅳ））与文献实验值DExp（U（Ⅳ））对比Fig.2 A comparison of three models by plotting calculated DCal（U（Ⅳ））against experimentally obtained DExp（U（Ⅳ））in UO2（NO3）2-U（NO3）4／HNO3-N2H5NO3／30%TBP-OK system

通过以上数据的验证可以得到以下结论：（1）除少数条件外，3种模型的计算值与实验值均存在较大偏差；（2）与印度研究者在其文献［8］中报道的结果相反，模型1的计算值偏差并未达到103以上，能够较为准确的预测U（Ⅳ）分配比走向，而印度的分配比模型（模型2）却偏差极大，根本无法用于计算U（Ⅳ）分配比；（3）模型1在计 算U（NO3）4／HNO3-N2H5NO3／30%TBP-OK萃取体系下的U（Ⅳ）分配比时，大部分计算值均小于实验值，产生负偏差，偏差来源可能是由于在该体系下，U（Ⅳ）对总硝酸根浓度的贡献值比计量比的值大；（4）模型1在计算UO2（NO3）2-U（NO3）4／HNO3-N2H5NO3／30%TBP-OK萃 取体系时，计算值与实验值的偏差分布均匀，能够用于模拟U（Ⅳ）分配比，但偏差较大；（5）模型3在计算两种萃取体系下的U（Ⅳ）分配比值时与实验值的偏差极大，也无法用于U（Ⅳ）的分配比计算。

因此，选用模型1为基础，通过修正以期得到更加可靠的分配比模型函数。

图3 U（NO3）4／HNO3-N2H5NO3／30%TBP-OK萃取体系下模型实验值与计算值比值随平衡水相硝酸浓度变化情况Fig.3 A comparison of modified models by plotting DExp（U（Ⅳ））／DCal（U（Ⅳ））against HNO3concentration in the equilibrium aqueous phase in U（NO3）4／HNO3-N2H5NO3／30%TBP-OK system

3.2 模型修正及方法

3.2.1 U（NO3）4／HNO3-N2H5NO3／30%TBPOK萃取体系下的模型修正 在U（NO3）4／HNO3-N2H5NO3／30%TBP-OK萃取体系下，模型1的计算值均小于实验值，将实验值除以模型计算值，得到的结果示于图3。经统计，在所有的253组数据中，实验值与计算值的比值小于0.7的数据共19组，只占该区域内数据的7.5%，大于2.0的数据共3组，只占该区域内数据的1.1%，比值在1.0至1.5之间的数据为190组，占该区域内数据的75%。因此，根据不同数据的权重，可得到该组数据的加权平均值为1.4，从而模型1可修正为：

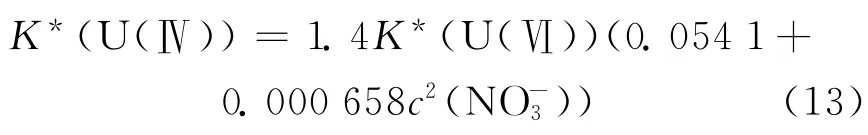
修正后的模型计算值与实验值的对比情况示于图4。通过图4可知，修正后的模型函数能够用于模拟计算U（NO3）4／HNO3-N2H5NO3／30%TBP-OK萃取体系下的U（Ⅳ）分配比。模拟计算值与实验值的偏差均在±10%以内。

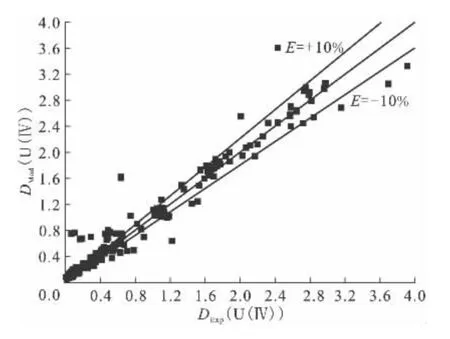
图4 U（NO3）4／HNO3-N2H5NO3／30%TBP-OK萃取体系下修正后的模型计算值DMod（U（Ⅳ））与实验值DExp（U（Ⅳ））的对比Fig.4 A comparison of modified models by plotting calculated DMod（U（Ⅳ））against experimentally obtained DExp（U（Ⅳ））in U（NO3）4／HNO3-N2H5NO3／30%TBP-OK system

3.2.2 UO2（NO3）2-U（NO3）4／HNO3-N2H5NO3／30%TBP-OK萃取体系下的模型修正 利用UO2（NO3）2-U（NO3）4／HNO3-N2H5NO3／30%TBP-OK萃取体系下的357组数据对修正后的公式（13）进行验证，验证结果示于图5。通过与UO2（NO3）2-U（NO3）4／HNO3-N2H5NO3／30%TBP-OK萃取体系下的U（Ⅳ）实验值相比，修正后的模型函数计算值偏高，且U（Ⅵ）在平衡水相中浓度越高，偏离的值越大，说明U（Ⅵ）浓度增加会减小U（Ⅳ）的分配比值，因此，拟将公式（13）改为形如式（14）的函数：

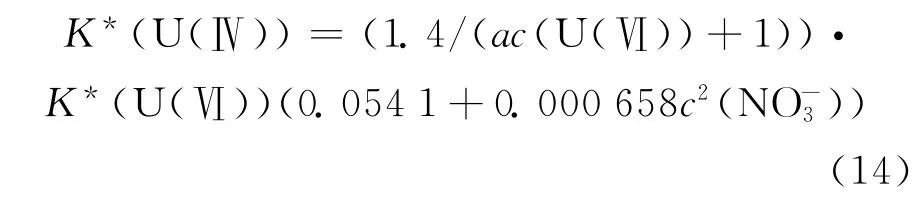
式（14）中的a为待定系数，c（U（Ⅵ））是平衡水相中U（Ⅵ）的摩尔浓度。经拟合得到的系数a为30，修正后的函数计算值与实验值的对比示于图6。通过图6可知，修正后的U（Ⅳ）分配比模型函数计算值与实验值间的相对误差大部分在±15%以内，比模型1的计算准确性有所提高。

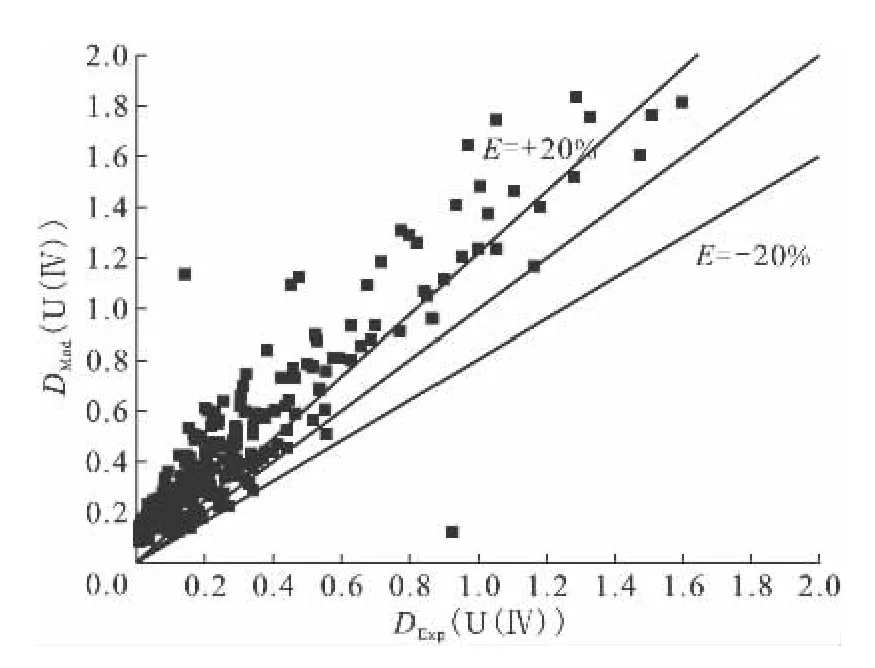
图5 UO2（NO3）2-U（NO3）4／HNO3-N2H5NO3／30%TBP-OK萃取体系下公式（13）对U（Ⅳ）计算修正值DMod（U（Ⅳ））与实验值DExp（U（Ⅳ））对比情况Fig.5 A comparison of modified models（13）by plotting calculated DMod（U（Ⅳ））against experimentally obtained DExp（U（Ⅳ））in UO2（NO3）2-U（NO3）4／HNO3-N2H5NO3／30%TBP-OK system

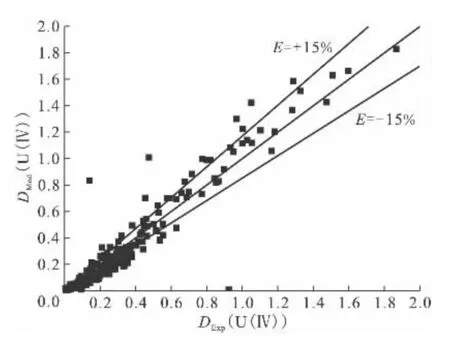
图6 UO2（NO3）2-U（NO3）4／HNO3-N2H5NO3／30%TBP-OK萃取体系下公式（14）对U（Ⅳ）计算修正值DMod（U（Ⅳ））与实验值DExp（U（Ⅳ））对比情况Fig.6 A comparison of modified models（14）by plotting calculated DMod（U（Ⅳ））against experimentally obtained DExp（U（Ⅳ））in UO2（NO3）2-U（NO3）4／HNO3-N2H5NO3／30%TBP-OK system

3.3 修正后的模型验证

选用UO2（NO3）2-U（NO3）4-Pu（NO3）3／HNO3-N2H5NO3／30%TBP-OK萃取体系下的22组数据［6］对修正后的模型函数公式（14）进行验证，验证结果示于图7。22组数据涵盖的平衡水相浓度范围分别为：HNO3浓度为0.7～1.5mol／L，U（Ⅳ）质量浓度为7.6～30g／L，U（Ⅵ）质量浓度为0.6～8.7g／L，Pu（Ⅲ）质量浓度为0.4～36.3g／L。通过图7可知，修正后的模型函数对UO2（NO3）2-U（NO3）4-Pu（NO3）3／HNO3-N2H5NO3／30%TBPOK萃取体系的U（Ⅳ）分配比计算值与实验值的偏差在±15%以内，从而该模型能够用于铀钚分离工艺段含Pu（Ⅲ）的分配比计算。

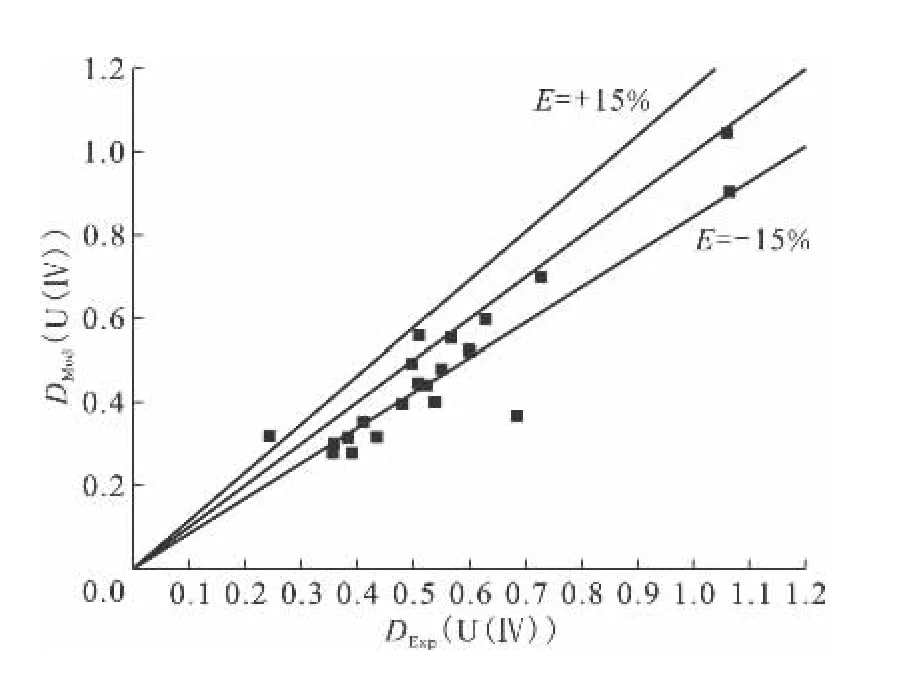
图7 UO2（NO3）2-U（NO3）4-Pu（NO3）3／HNO3-N2H5NO3／30%TBP-OK萃取体系下公式（14）对U（Ⅳ）计算修正值DMod（U（Ⅳ））与实验值DExp（U（Ⅳ））对比情况Fig.7 A comparison of modified models（14）by plotting calculated DMod（U（Ⅳ））against experimentally obtained DExp（U（Ⅳ））in UO2（NO3）2-U（NO3）4-Pu（NO3）3／HNO3-N2H5NO3／30%TBP-OK system

4 结 论

通过以上分析，得到以下结论：

（1）文献中发表的U（Ⅳ）分配比模型在模拟计算U（Ⅳ）分配比值时均存在较大的偏差，其中美国研究者发表的模型以Richardson分配比模型为基础，为半理论模型，模拟效果是已发表模型中最好的；

（2）以美国研究者发表的模型为基础，通过多组U（Ⅳ）分配比数据对该模型进行修正及验证，最终得到的U（Ⅳ）分配比模型为：D（U（Ⅳ））＝K＊（U（Ⅳ））c2（fTBP），其中K＊（U（Ⅳ））＝（1.4／（30c（U（Ⅵ））＋1））K＊（U（Ⅵ））（0.054 1＋0.000 658×c2（））。式中c（U（Ⅵ））代表平衡水相中U（Ⅵ）的摩尔浓度，K＊（U（Ⅵ））代表U（Ⅵ）的表观平衡常数，c）代表平衡水相中的总硝酸根浓度；

（3）修正后的模型函数的适用范围为：平衡水相硝酸浓度为0.4～4.0mol／L，U（Ⅳ）质量浓度为5～50g／L，U（Ⅵ）质量浓度为15～150g／L，Pu（Ⅲ）质量浓度为0.4～36.3g／L，肼浓度为7×10-4～2mol／L，相对偏差在±15%以内。

［1］陈延鑫，何辉，唐洪彬，等.后处理工艺Purex流程计算机模拟研究现状及展望［J］.核化学与放射化学，2012，34（4）：193-200.

［2］何辉，李高亮，陈辉，等.Purex流程共去污工艺计算机稳态模拟［J］.原子能科学技术，2008，42（9）：784-789.

［3］Richardson G L，Swanson J L.Plutonium partitioning in the Purex process with hydrazine-stabilized hydroxylamine nitrate：HEDL-TME-75-31［R］.USA：OAK Ridge National Laboratory，1975.

［4］陶 成 英，费 洪 澄.UO2（NO3）2-U（NO3）4-HNO3／30%TBP-煤油体系萃取平衡分配数据的测定［J］.原子能科学技术，1988，22（2）：185-192.

［5］Petrich G，Kolarik Z.The 1981Purex distribution data index：KfK-3080［R］.Germany：Kernforschungszentrum Karlsruhe，1981.

［6］Tachimori S，Nakashima T，Kolarik Z，et al.Distribution of U（Ⅳ），U（Ⅵ），Pu（Ⅲ）and nitric acid between 30vol.%tributyl phosphate in dodecane and aqueous nitrate solutions：KfK-3637［R］.Germany：Kernforschungszentrum Karlsruhe，1983.

［7］Geldard J F，Phillips L，Beyerlein A L.Correlation functions for the distribution coefficients of U（Ⅳ）and Pu（Ⅲ）ions between aqueous nitric acid and 30%TBP in an aliphatic diluent［J］.Nucl Technol，1985，70：394-400.

［8］Kumar S，Koganti S B.Empirical modeling of U（Ⅳ）distribution in a nitric acid-water-30%TBP／n-dodecane biphasic system in the presence of U（Ⅵ），Pu（Ⅲ），and hydrazine nitrate［J］.Nucl Technol，1998，123：116-119.

［9］Gonda K，Oka K，Fukuda S.Calculation code revised mixset for Purex process：PNC-TN841-79-26［R］.Japan：Power Reactor and Nuclear Fuel Development Corporation，1979.

［10］Tsubata Y，Asakura T，Morita Y.Development of a computer code，PARC，for simulation of liquidliquid extraction process in reprocessing：JAEAData／Code-2008-010［R］.Japan：Atomic Energy Agency，2008.