共去污单元脉冲萃取柱模型及计算机模拟

于 婷，何 辉，陈延鑫，唐洪彬，彭 力，王立京

1.中国科学院 上海应用物理研究所，上海 201800；

2.中国原子能科学研究院 放射化学研究所，北京 102413；

3.中国原子能科学研究院 劳动人事教育处，北京 102413

乏燃料后处理Purex流程是由多个萃取分离循环组成，其中铀钚共去污工艺是整个化学分离过程的关键环节之一，该单元是利用U（Ⅵ）和Pu（Ⅳ）可被磷酸三丁酯（TBP）萃取的性质将它们与绝大部分的裂变产物和超铀元素分开，运行工况会影响最终产品的质量、金属的收率等。共去污单元操作的主要特点是：含有大量的杂质和裂片元素，处理料液放射性活度高容易造成溶剂辐解从而形成界面污物，因此该工艺段的萃取设备只能选用液体停留时间短、界面污物易排除的脉冲萃取柱［1-4］。

在共去污单元中，同时存在铀、钚、硝酸裂片元素等多种组分，溶质通过含有硝酸的水相与TBP-煤油有机相逆流接触进行相际间传质。组分在两相间的分配由传质速率和化学平衡来确定，其中操作温度、各组分浓度和两相接触情况均影响传质速率和化学平衡，所以，共去污是一个复杂的萃取过程。为了对萃取器的分离效率做出正确的估计，计算萃取各组分浓度剖面，人们力图使用数学方法模拟萃取过程进行研究以指导实验和生产［5］。但是数学模拟方法计算繁杂，人工计算无法胜任。计算机的广泛应用为萃取过程的数学模拟研究提供了一种十分便利的工具，它不但可以计算各液流的出口浓度、萃取器各级的浓度，还能够透视萃取设备中的动态过程，因此，计算机模拟成为后处理中流程设计、优化和安全分析的有效工具。国内外已开发了许多程序，诸如PARC、SEPHIS以及PULCO等用于模拟优化后处理工艺［6］。

目前脉冲萃取柱的计算机模拟研究多以扩散模型为基础，该模型能够反映出柱内流体流动和传质情况，模型公式有实际的物理意义［7］，但在共去污单元多组分萃取时，分配比是两相组分浓度的复杂函数，以往的模型并未解决分配比计算问题，因此无法求解共去污单元多组分萃取问题。本工作在扩散模型的基础上，将分配比模型计算引入以克服原模型计算使用常数分配比等缺点，拟编写HNO3、U（Ⅵ）、Pu（Ⅳ）体系模拟程序，并利用文献报道的实验数据和计算数据，对该程序进行验证。

1 计算原理

Purex流程共去污工艺单元中，主要的操作为萃取和洗涤，本工作仅对萃取过程加以模拟计算，在萃取过程使用有机相作为连续相，水相作为分散相。以往对于脉冲萃取柱的模拟计算都是对柱内的各组分列偏微分方程组，然后对方程进行差分离散化求解，这种方法可以将偏微分方程转化成为线性方程从而进行求解，但在离散化过程中忽略了柱内轴向方向的各组分浓度是呈连续变化的，对于各组分分配比是组分浓度的复杂函数进行粗略简化，这样只能求解得到单组分时的扩散模型，对于多组分求解则不准确。若是将分配比模型计算公式直接代入扩散模型偏微分方程组，则无法得到方程合理的实数根，因此本工作对脉冲萃取柱进行数学处理，即将脉冲萃取柱在沿轴向方向“切片化”处理，认为每一个“切片”内的各个组分的分配比为一定值，然后对每个切片列得偏微分方程组求解，这样则克服了分配比求解的困难。

1.1 传质模型

扩散模型假定在脉冲萃取柱内的传质过程包括相际间传质和连续相中由于存在浓度梯度而导致的扩散传质，模型认为在有机相中存在高浓端向低浓端的传质过程，溶质在柱高方向的传质速率和该相内组分浓度梯度成正比，称为有机相的轴向扩散［8］。扩散模型将两相流动的非理想性归结于轴向扩散系数，整个扩散过程符合Fick定律。图1为扩散模型示意图。

图1中表示的两相逆流接触（假设Y相为连续相），取其中一个微元做物料衡算，设向上为正方向，柱子横截面积为S，有机相存留分数为φ，微元高为dz，两相液体流速为ux、uy在柱内不发生变化，Ey为连续相轴向扩散系数，则对连续相进行微元内物料衡算可以得到以下方程组：

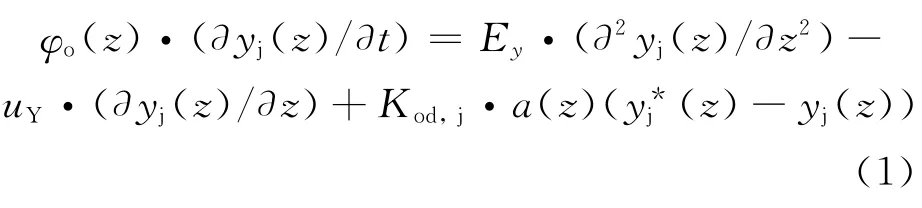
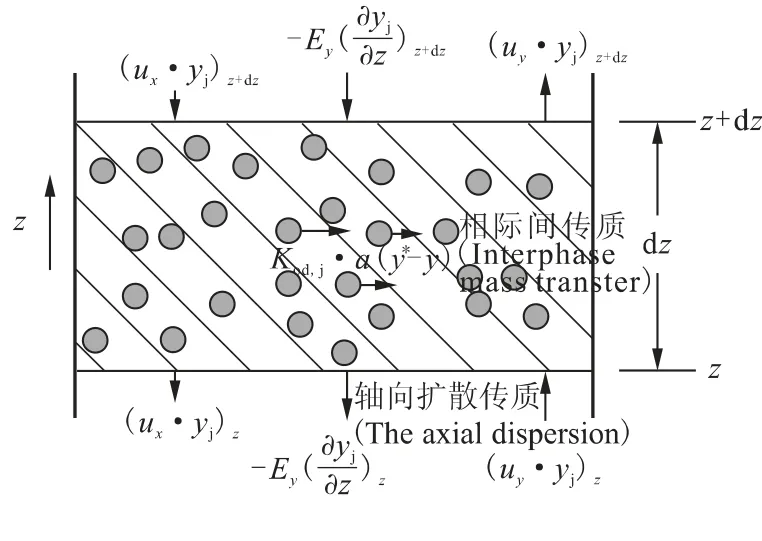
图1 扩散模型示意图Fig.1 Dispersion model

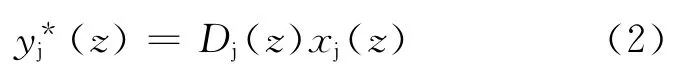
Ey，轴向扩散系数；a（z），传质表面积；uY，连续相流速；yj＊（z），j组分有机相平衡浓度；xj（z），j组分水相浓度；Dj（z），分配比。

方程组的初始条件以及边界条件为：

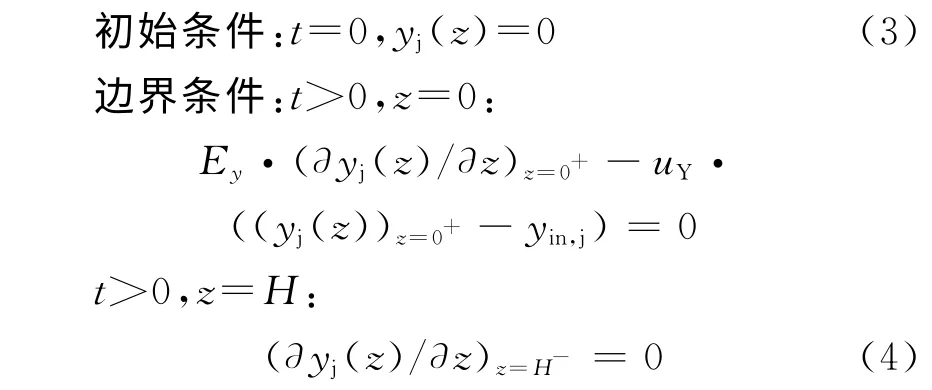
其中，连续相轴向扩散系数Ey和传质表面积a（z）采用文献［8］中经验计算公式计算得到，连续相流速uY根据脉冲柱结构计算得到。

1.2 分配比模型

近30年来，对于铀、钚、酸体系的分配比方面的研究已经获得了大量的数据，对这些数据进行拟合，已经得到许多分配比模型［3］，且大部分分配比模型的建立均考虑Mm＋在TBP-HNO3体系中的萃取反应：

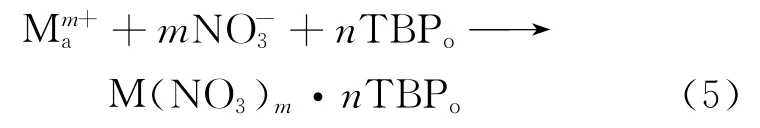
一般Mm＋会形成M（NO3）m·nTBPo络合物被萃入TBP中，反应的热力学平衡常数K为：

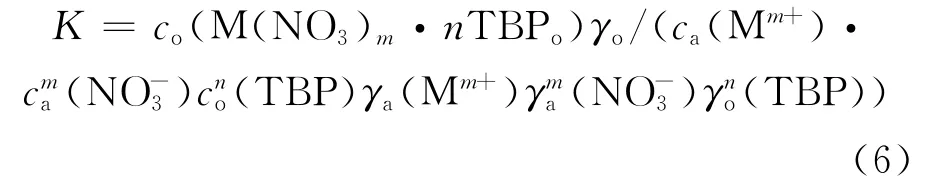
式中：c为摩尔浓度，mol／L；γ为活度系数；小角标a、o分别表示水相、有机相。

定义分配比D（M）为：

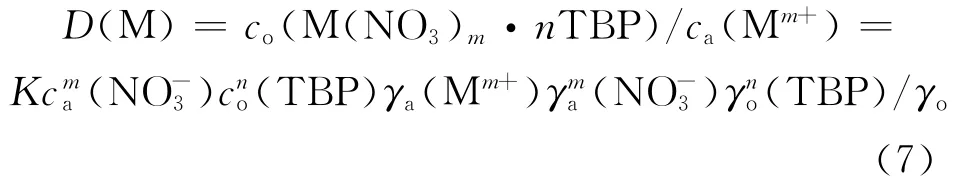
当Mm＋浓度极低时，K为定值。于是，有下式成立：

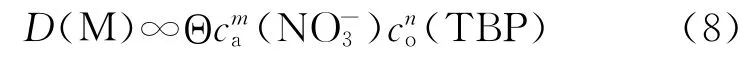
式中：Θ为常数。当体系中的硝酸浓度或金属离子Mm＋的浓度较高时，各组分的活度系数不再保持不变。各组分在水相、尤其在有机相中的活度系数数据缺乏，但人们获取了这些组分大量的分配比数据。为此，引入表观平衡常数K＊（M）：

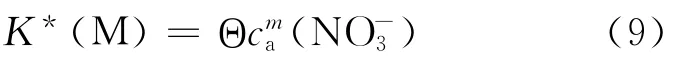
通过拟合大量分配比数据，可方便的将K＊（M）关联成水相硝酸根总浓度c（）的函数。）可表示为：

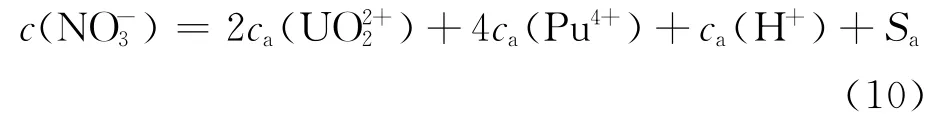
式中：Sa为水相溶液中不被有机相萃取的其他组分的总盐浓度。

数学回归得到25℃、30%TBP下的表观浓度平衡常数K25＊为：

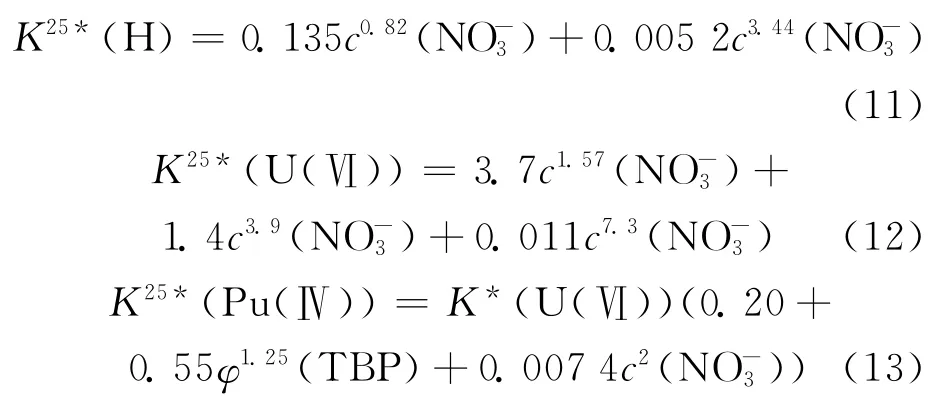
式中，φ（TBP）为TBP体积分数。在Purex流程共去污段中，大部分都使用φ（TBP）＝30%萃取剂。但针对不同燃耗、不同类型的乏燃料元件的后处理所采用的TBP浓度不同，比如英国的Sellafield后处理厂使用φ（TBP）＝20%萃取剂；高浓燃料的后处理还可能使用φ（TBP）＝4%～5%为萃取剂。所以，萃取剂浓度以及温度对分配比的影响必须加以考虑。

其它温度和TBP浓度下的K＊（M）如下：

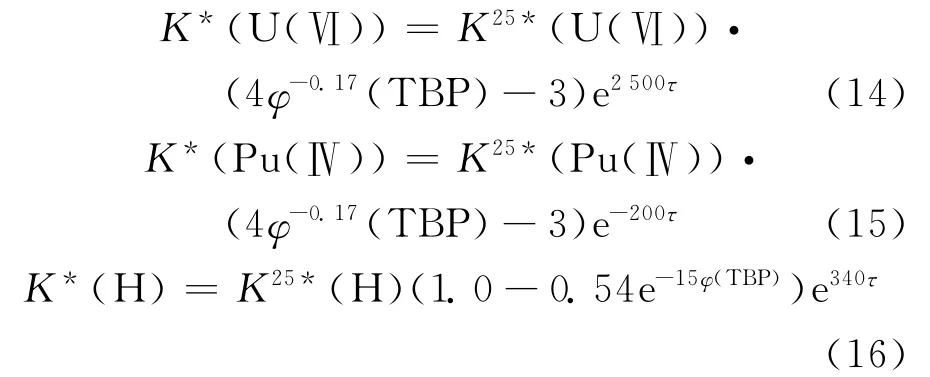
各组分的分配比进而可由下式得到：

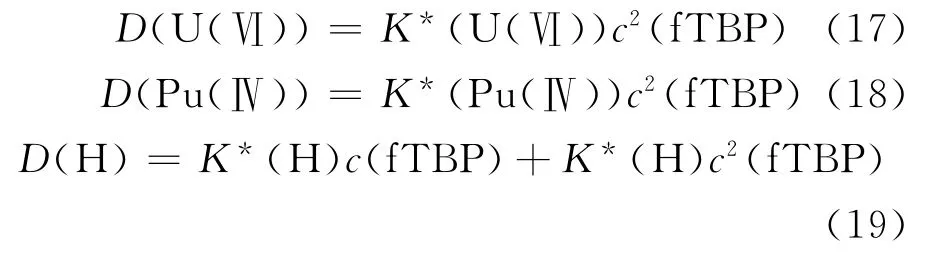
式中：c（fTBP）为自由TBP的浓度，可通过对TBP进行物料衡算得到：

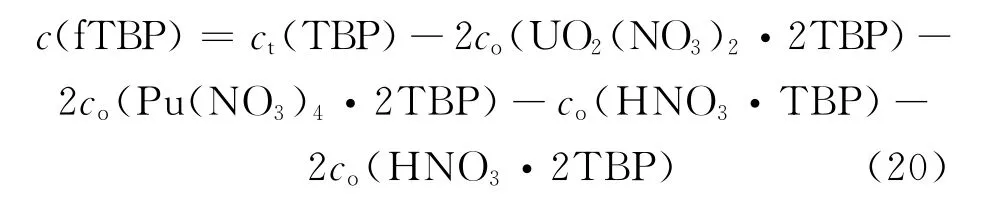
将以上各式代入式（20）整理后可得：

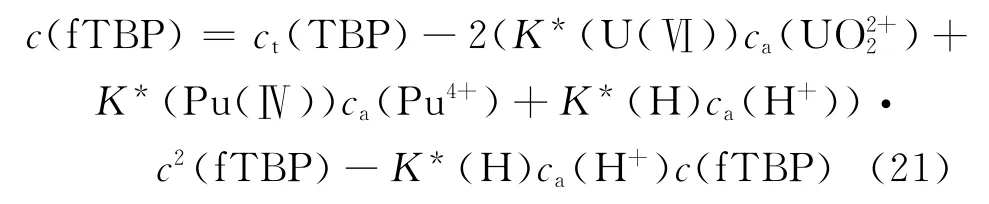
这里ct（TBP）＝3.651φ（TBP）。

式（21）为二次方程，其合理解（另一解为负值）可通过下式求出：

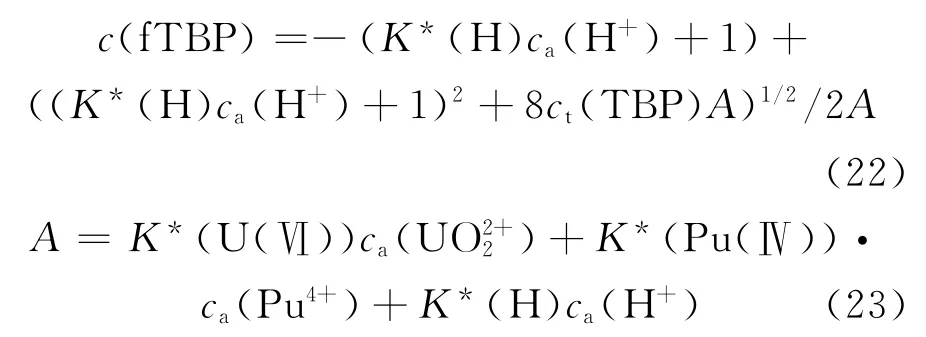
利用此分配比模型计算微分萃取段两相的平衡浓度必须知道平衡水相中各组分的浓度，因此对于脉冲萃取柱中不同的微分萃取段的平衡浓度要使用一定的算法得到。在分配比模型中，计算分配比需要知道平衡浓度，而平衡浓度也为待求值，而且此值与分配比也有关系，故在仅知两相进料浓度的前提下，对于平衡浓度和分配比的求取使用迭代计算的方法进行求解，即将脉冲柱每段的连续相进料浓度和分散相进料浓度作为输入条件，然后迭代求解。模块流程图示于图2。

编写程序时，将分配比以及平衡浓度的计算单独列出函数，称为分配比计算模块，在每一段计算时首先调用该模块求得每一段内两相各组分的分配比和平衡浓度。

1.3 模型算法

在扩散模型为传质模型的基础上，则可对脉冲萃取柱建立数学模型，模型假设：在柱高方向将脉冲柱分为多段，“切片”化处理，认为在每个切片内各组分的分配比、分散相液滴粒径以及存留分数等为固定值；两相体积流量在柱内保持不变；相邻的两个切片间认为只存在流体的流入流出，不考虑传质和连续相轴向扩散，每个“切片”内的分散相浓度采用物料衡算方法求解。

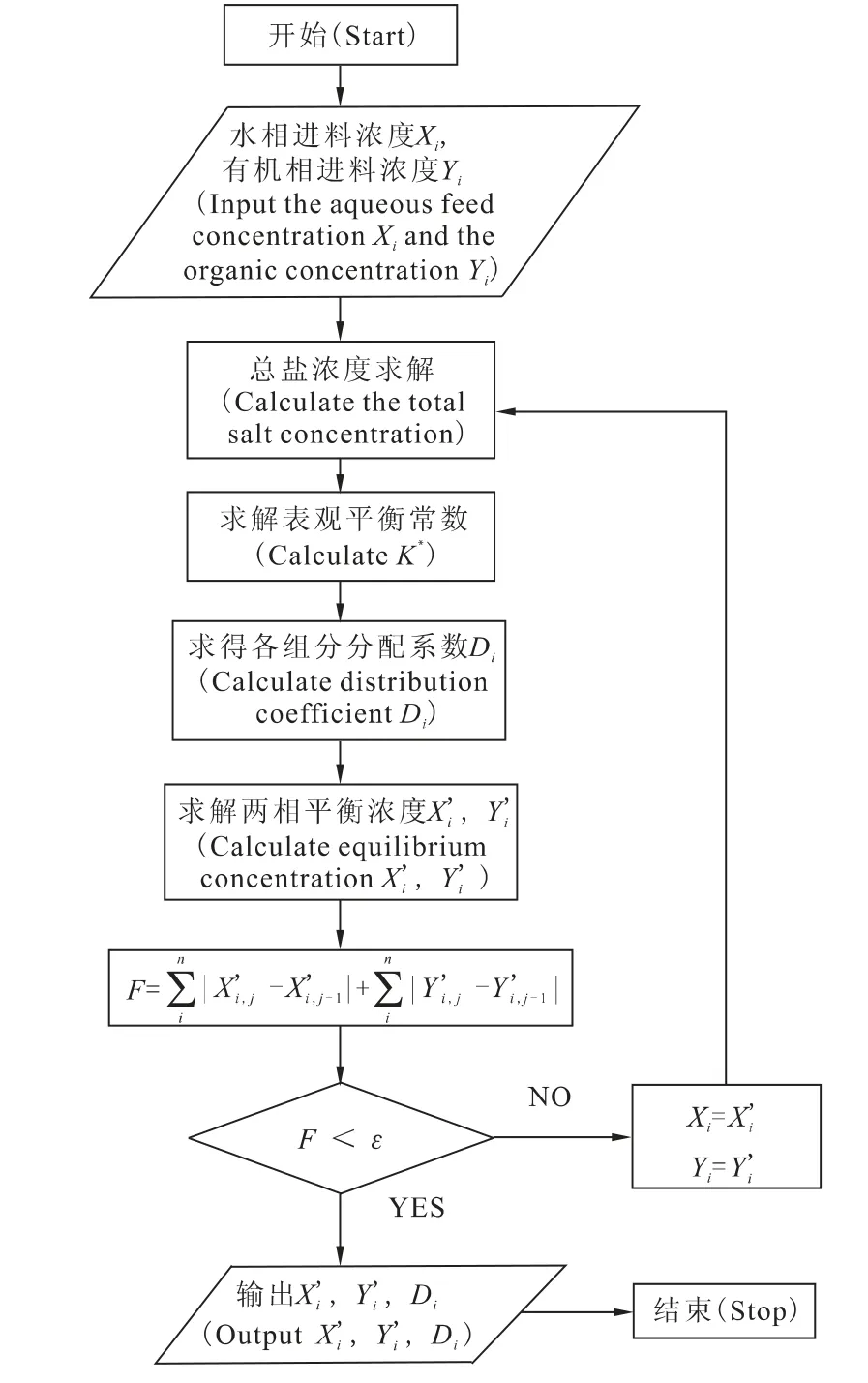
图2 分配比模型计算流程图Fig.2 Calculation flowchart of partition coefficient

图3 脉冲萃取柱萃取示意图Fig.3 Schematic diagram of extraction

图3中左图即为将脉冲萃取切片化处理后的示意图，因两相流速、各组分分配比在每个切片内都保持不变，则每个切片计算之处都调用一次分配比计算模块，这样用于扩散模型计算的分配比比整个柱体一个分配比进行计算要准确的多，并且可以进行多组分共存萃取计算，分配比计算完成后，则可以依次对每一个“切片”进行差分离散化求解，如图3右图所示，最终得到每一“切片”上下两端的两相出口浓度，将所有的切片的计算结果按照一定的方式组合起来，则可得到整个脉冲萃取柱的计算结果，组合方式即为模型的迭代算法。

图4所示的算法结合了共去污段萃取过程脉冲萃取柱的运行过程，其所示的单位时间t不是随意指定的时间，是两相流体流过指定高度的每一级所需要时间的最大值，算法具体为：

（1）t＝0时段：连续相（有机相）流体将充满柱体，此时整个脉冲柱内只存在有机相浓度Yin，此时是分散相（水相）即将进入柱体的临界时间；

（2）t＝1时段：分散相进入第一段，如t＝1图所示，在级内发生扩散传质，首先根据两相进口浓度计算得出分配比和两相平衡浓度，并对有机相列扩散传质偏微分方程，级高h两侧已知的输入值Xin和Yin即为扩散模型偏微分方程的边界（B.C.）条件，进行求解后得到连续相（有机相）级出口端输出值Y1，1，并根据物料守恒求解得到分散相出口端值X1，1；

（3）t＝2时段：t＝1时段的分散相X1，1流入柱体下端相邻级，并在其中发生扩散传质，进行计算可以得到该级的有机相出口浓度Y2，1和分散相出口浓度X2，1，此时段2h处也发生扩散传质，与h处不同的是，段两端的两相入口浓度不同，导致传质推动力不同，因而各个组分传质量是不同的，经过计算可以得到2h的两相出口浓度，即Y2，2和X2，2；

（4）t＝n时段：此时段是分散相恰好运行满柱的时段，各个段的输入输出浓度如t＝n图所示，每一级计算开始都调用分配比计算函数计算分配比和两相平衡浓度，并对每一级分别进行微分计算，最终得出两相出口处的浓度；

（5）t＝∞时段：脉冲萃取柱达到稳态，柱内两相浓度剖面不再改变，程序判断达到稳态的条件即为同级的两相出口浓度不再变化，如图中t＝k-1时段和t＝k时段所示。

脉冲萃取柱模拟算法流程图示于图5。

图4 迭代算法示意图Fig.4 Iterative algorithm of the model

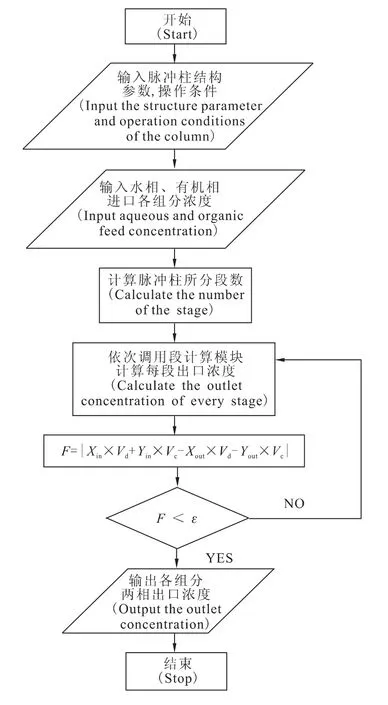
图5 脉冲萃取柱模拟算法流程图Fig.5 Calculation flowchart of column iterative algorithm

1.4 程序编写

使用Matlab语言编写计算机程序。程序在Intel Pentium1.87GMZ、2.00GB内存的电脑调试通过。

2 结果与讨论

文献报道了Purex流程计算模拟程序PULCO［8］的设计，描述了程序的验证实验工艺条件，同时对实验值和程序计算值进行了比较，验证实验设备的结构参数为：内径φ50mm，脉冲萃取柱柱高200cm；筛板结构：筛板数36，筛板孔径φ0.3cm，自由截面积23%；操作条件：每循环脉冲振幅1.8cm，每分钟40次脉冲频率。

工艺条件分别为：水相进料浓度：HNO33.2mol／L，U（Ⅵ）97g／L，Pu（Ⅳ）8.3g／L；有机相进料为30%TBP（煤油）；水相进料流速为6.8L／h，有机相进料流速为13.2L／h。

这样，本工作使用Matlab语言编写了计算机程序，并以文献报道的数据条件作为程序初始条件模拟计算，将计算结果与实测值进行比对，从而对程序进行验证。此外还与PULCO程序的计算结果［8］进行比对，具体如图6所示。

图6表明，在有机相出口处，HNO3的计算偏差为2.3%，U（Ⅵ）的计算偏差为-6.8%，Pu（Ⅳ）的计算偏差为-8.6%，均小于10%；PULCO程序的计算偏差硝酸为13.9%，U（Ⅵ）为-3.46%，Pu（Ⅳ）为-2.2%，HNO3在有机相入口端计算偏差偏大，分析原因可能是计算模型采用的HNO3传质模型存在偏差。但是，可以得出以下结论：本工作对共去污段脉冲萃取柱所建立的数学模型，即切片化计算各组分分配比，所建立的考虑连续相轴向扩散系数的扩散模型以及提出的迭代算法可以实现HNO3、U（Ⅵ）、Pu（Ⅳ）多组分共萃的计算。

图6 U（Ⅵ）（a）、Pu（Ⅳ）（b）、HNO3（c）程序计算值与实验值比对图Fig.6 A comparison of concentration profiles calculated by PULCO and this work with experiment values of U（Ⅵ）（a），Pu（Ⅳ）（b）and HNO3（c）

3 初步工艺研究

应用于后处理的脉冲萃取柱的放大设计一直依赖于理论级当量高度HETS（height equivalent of a theoretical stage）和传质单元高度HTU（height of a transfer unit）等基于混合澄清槽方面的参数［9］。使用本工作程序与中国原子能科学研究院何辉等［3］开发的已通过实验验证的1A混合澄清槽模拟程序，完成对柱高设计计算中混合澄清槽与脉冲萃取柱的对应性研究。

计算以U（Ⅵ）为基准、以进料浓度为横坐标、等同于一级混合澄清槽萃取效率的脉冲萃取柱柱高为纵坐标，脉冲萃取柱与混合澄清槽对应性研究结果示于图7。由图7可知，随着水相进料铀浓度的增加，等同一级混合澄清槽的脉冲柱柱高越小，脉冲柱的萃取效率越大，分析原因可能是水相铀浓度越高，其分配比越小，这个结果与PULCO［8］报道的结论基本相符。

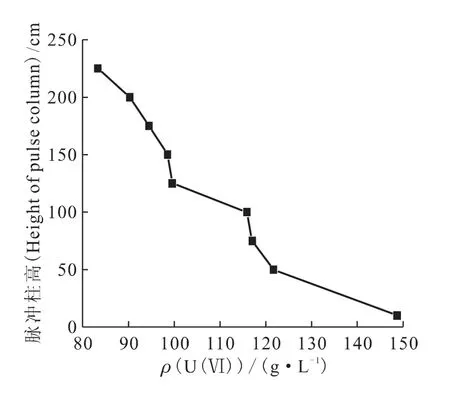
图7 脉冲萃取柱与混合澄清槽对应性研究Fig.7 Height equivalent to a single mixer-settler stage for a pulsed extraction column

因此，通过以上计算结果可知，在脉冲萃取柱的设计中，单纯按照若干米柱子对应一级混合澄清槽这种经验式设计方法有其不合理性，因在脉冲萃取柱中，水相以及有机相中的铀浓度是梯度分布的，并不是均一不变的，则不同柱高处对应的槽子级数并不相同，这样使用平均值设计的脉冲萃取柱，会使得柱高偏大，从而造成设计浪费。实际上，在设计脉冲柱时，应将连续萃取的脉冲柱整体考虑，尤其是组分的分配比在沿轴向分布较广的情况时，柱高设计就不应该单纯的使用经验高度进行，而是应该使用脉冲柱程序来进行相关计算。

4 结 论

本工作对应用于共去污单元的脉冲萃取柱“切片化”抽象处理后，对其建立扩散传质模型，将分配比计算模型嵌入完成数学模型，编写了计算机程序。此程序计算结果与文献报道值符合良好，基本可以实现共去污段多组分共萃的计算。将程序应用于脉冲萃取柱的工艺设计的初步研究，得到以往使用一级混合澄清槽萃取效率等于若干米柱高的设计方法有待商榷，在柱高的设计方面应将脉冲萃取柱整体考虑，应使用计算机模拟方法进行整体设计。

［1］姜圣阶.动力堆核燃料后处理厂设计［M］.北京：原子能出版社，1996.

［2］姜圣阶，任凤仪，等.核燃料后处理工学［M］.北京：原子能出版社，1995.

［3］何辉，李高亮，陈辉，等.Purex流程共去污工艺计算机稳态模拟［J］.原子能科学技术，2008，42（9）：784-789.

［4］陈延鑫.核燃料后处理工业中脉冲萃取柱的计算机模拟研究［D］.北京：中国原子能科学研究院，2009.

［5］何辉.N，N-二甲基羟胺在铀钚分离中的应用和计算机程序的开发［D］.北京：中国原子能科学研究院，2001.

［6］张春龙.Purex流程中锝萃取行为的计算机模拟［D］.北京：中国原子能科学研究院，2011.

［7］唐晓津.分散-聚并脉冲筛板萃取塔的组合模型［D］.北京：清华大学，2005.

［8］Gonda K，Matsuda T.Solvent extraction calculation model for Purex process in pulsed sieve plate column［J］.J Nucl Sci Technol，1986，23（10）：883-895.

［9］王俊峰.核燃料后处理工程溶剂萃取设备［M］.北京：原子能出版社，2012.