采用LCL并网逆变器的微电网双闭环并网控制策略研究

郑飞扬，张云红，杨 敏

(国网重庆綦南供电公司，重庆401420)

微电网的快速发展催生了并网逆变器等电力电子器件在电网中的大量应用。但是广泛使用逆变器之类的电力电子器件将会产生大量的谐波，使并入大电网的电能质量受到严重影响［1］。因此，就需要使用滤波器来过滤掉这些谐波。

并网逆变器采用的滤波器通常有两种:L滤波器和LCL滤波器。电感值相同的情况下，在低频段两种方式的滤波器滤波效果相同，但在高频段，LCL滤波器的滤波效果明显好于L滤波器。若要增加L滤波器在高频段的滤波能力，就必须增加其电感值。由于电感的成本较高，因此两种滤波器的成本主要集中在电感上。所以，在采用相同电感值，成本差不多的情况下，LCL滤波器具有更好的滤波效果［2］。目前，LCL滤波器已经有逐渐取代L滤波器的趋势。虽然LCL滤波器有着上述的优点，但是，它作为一个三阶系统，容易产生谐振，造成系统的不稳定。在谐振频率附近其阻抗值接近于0，因此会产生巨大的谐振尖峰［3］。如果不能有效抑制谐振，将会造成系统不稳定。通常，抑制谐振有两种方式:一种是无源阻尼法，就是直接增加LCL滤波器的阻尼，比如在电容支路串接电阻，增加滤波系统的阻尼以抑制谐振［4］;另一种方法就是有源阻尼法，通过采取对电压电流的控制来实现抑制谐振的目的［5］。常用的有源阻尼法有:零极点配置控制、加权电流反馈控制、重复控制等［6］。采用无源阻尼法，无论是串接还是并联电阻，都会增加系统的额外损耗［7］。

本文研究采用有源阻尼法中的并网电流外环和电容电流内环的双闭环控制策略。

1 采用LCL滤波的单相并网逆变器的主电路结构与分析

采用LCL滤波的单相并网逆变器的主电路图如图1所示。

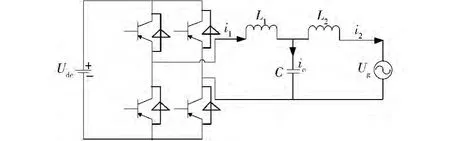
图1 采用LCL滤波的单相并网逆变器主电路图

微电网发电系统的直流电经逆变器逆变成正弦交流电输出，然后经LCL滤波器滤去高次谐波，最后接入大电网。其中，逆变器是通过脉冲宽度调制(Pulse Width Modulation，PWM)实现对其输出的控制。

2 并网电流外环电容电流内环的双闭环控制策略

基于LCL滤波器的单相并网逆变器的控制结构如图2所示。将逆变器的输出电压ui作为输入，并网电流i2作为输出。其传递函数为一个三阶系统。与L滤波器和LC滤波器相比，它具有更好的滤波能力。根据基尔霍夫定律(Kirchhoff's law)，LCL滤波器的暂态方程如下(忽略寄生电阻):

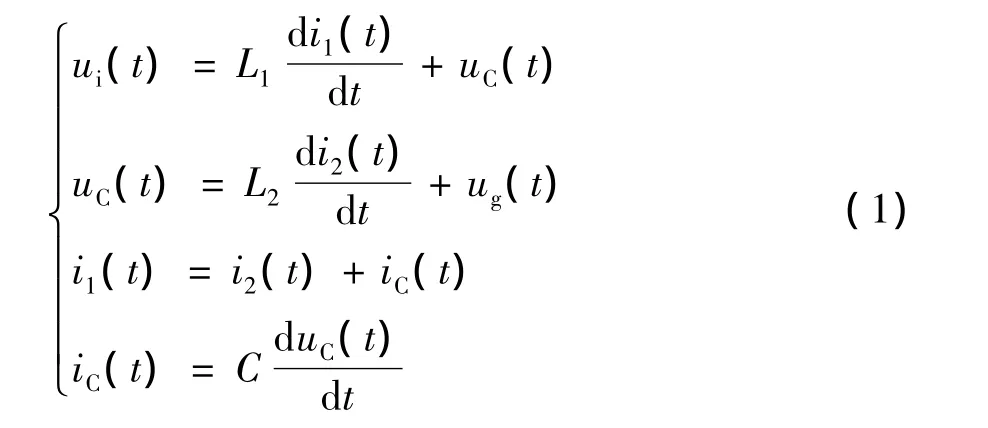
由暂态方程得到其控制框图如图2所示。

图中，G1(s)、G2(s)和 G3(s)分别为 1/sL1、1/sC 和1/sL2。

图2 采用LCL滤波的并网逆变器结构图

在低频情况下，LCL滤波器也相当于一个单电感滤波器，其电感值L为(L1+L2)。根据梅森公式(Mason formula)，其开环传递函数为:

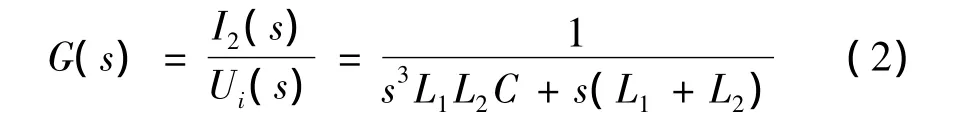
这里所提到的双闭环控制系统是以电容电流作为内环，并网电流i2作为外环。其控制框图如图3所示。图中，iref是i2的电流参考值;Gi(s)为 Kp+Ki/s，是一个PI控制器;GC(s)为KC，它是一个比例控制器。

图3 采用LCL滤波的并网控制策略结构图

根据并网控制的策略结构图，画出其开环传递函数的信号流图，如图4所示。

图4 信号流图

由信号流图和梅森公式得到其开环传递函数为:

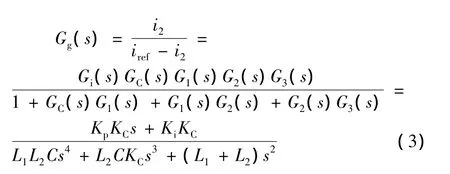
由此推得其闭环传递函数为:

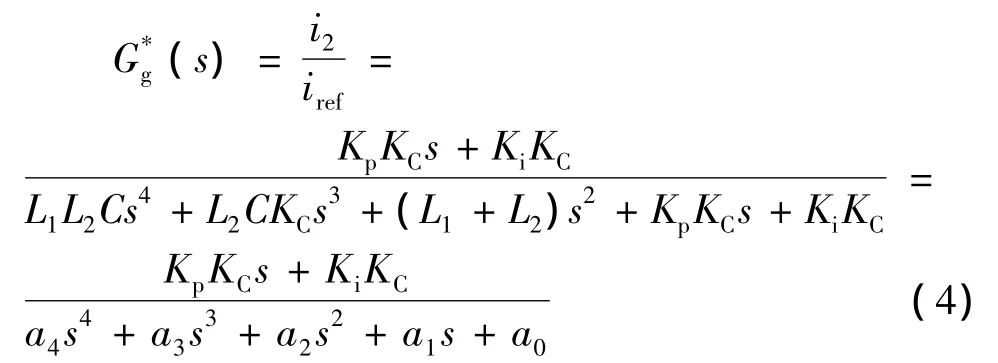
式中，a4为 L1L2C，a3为 L2CKC，a2为(L1+L2)，a1为KpKC，a0为 KiKC。

它的特征方程为:

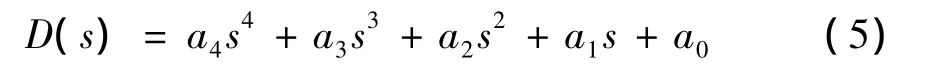
由此，可以知道它为一个四阶线性系统。它要稳定就必须保证所有的极点有负根或者负的实部，换一种说法就是此系统的所有极点都位于s平面的左半平面。如果该系统满足劳斯-赫维茨稳定性判据，那么就能保证它的极点在s平面的左半平面。根据上面方程，得到劳斯判据，如表1所示。

表1 劳斯-赫维茨稳定性判据

最后得出，要使系统稳定，特征方程的系数就必须满足下面的不等式组:

3 仿真结果及分析

在Simulink中建立的模型如图5所示。

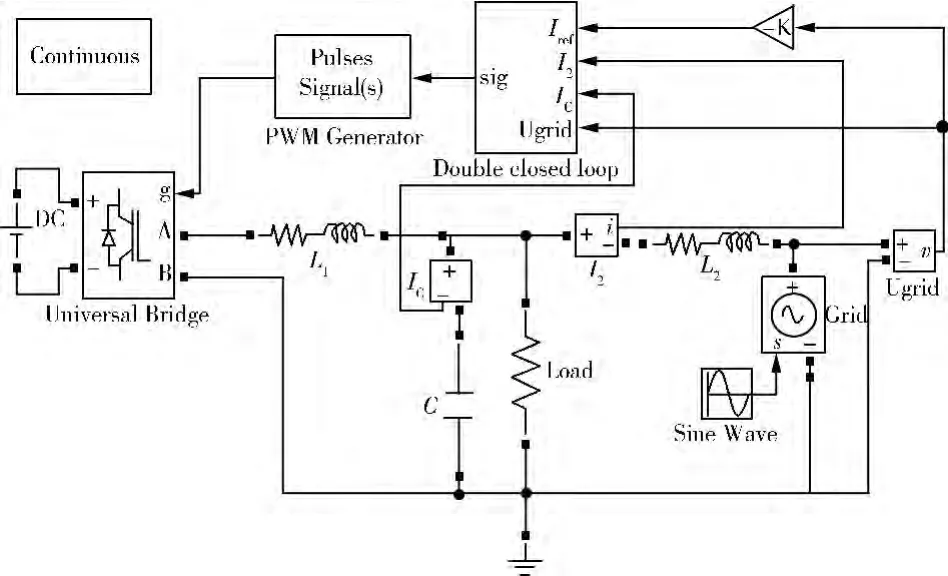
图5 并网模型仿真图

双闭环控制系统为本模型的核心，它的原理已经介绍。在Simulink中，其结构如图6所示。PI控制器的参数:Kp=2.43;Ki=98.1;KC部分也采用一个PI控制器，将比例系数的值设为100，积分系数的值设为0。

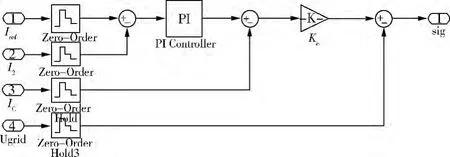
图6 双闭环控制框图

该仿真模型的主要参数:Udc=400 V;ug=311 V(50 Hz);L1=2 mH;L2=1 mH;C=2 μF;Kp=2.7;Ki=100;KC=100。

为验证该控制策略的特性，在两种情况下对模型进行了仿真:(1)微电网空载;(2)空载情况下，微电网在0.15 s时接入一个纯电阻负荷 (R=4.84 Ω)。

第一种是微电网空载的情况下，仿真结果如图7～图10所示。i2为并网电流;iref为参考电流。如图7所示，并网电流波形与参考电流波形几乎重合，这就证明该控制方法具有很好的控制效果。衡量并网发电电能质量有两个重要指标:并网电流总谐波畸变率和微电网的并网功率因数。总谐波畸变率越小，说明流入电网的谐波越少，电能质量越好;并网功率因数越高，送入大电网的有功功率也就越高。图8所示为并网电流i2与大电网电压ug的波形，它说明并网电流与大电网几乎保持相同的相位。所以，在并网情况下，该控制系统能够使微电网具有较高的并网功率因素，如图9所示。图10为并网电流的FFT谐波分析图，可以看出并网电流的有效值为32.76 A，总谐波畸变率(THD)为0.04%。同理，如图11～图14所示，在微电网运行时，中途加入负荷，并网电流经历短暂的振动后，很快恢复稳定，这种情况说明该控制策略具有较好的动态性能。

因此，通过仿真结果可以证明采用LCL滤波器的双闭环并网控制策略具有很好的控制效果和滤波性能。

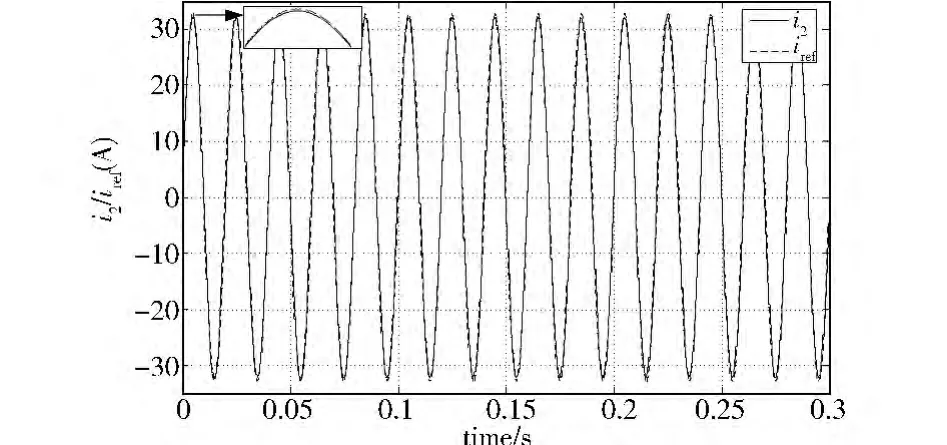
图7 微电网空载时的并网电流和参考电流波形图

4 总结

微电网的快速发展促使着相关控制策略的发展。在MATLAB/Simulink中，本文建立了一个采用双闭环控制策略的微电网仿真模型，仿真结果验证了该控制策略能够有效消除LCL滤波器带来的谐振问题。同时，它还具有很好的控制性能，能够满足微电网并网的要求。

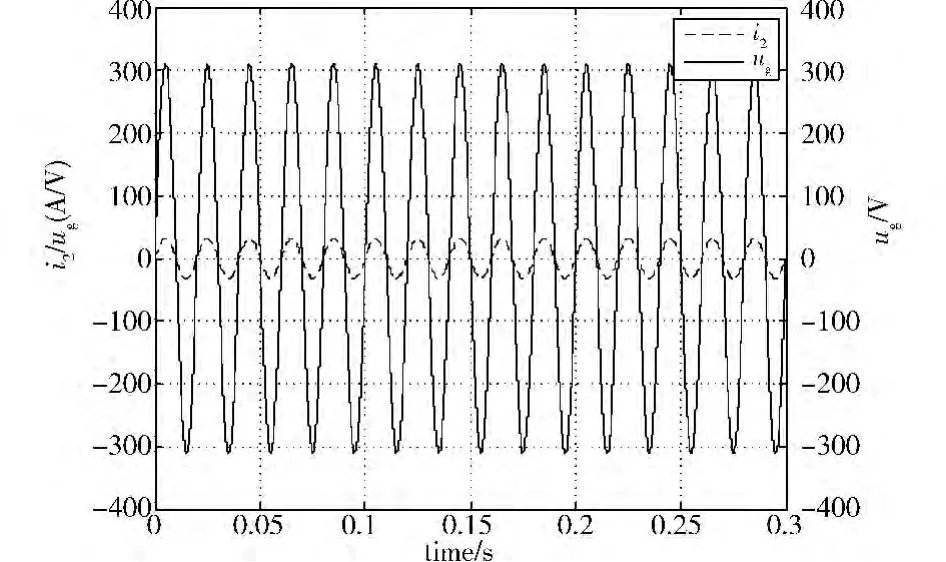
图8 微电网空载时的并网电流和大电网电压波形图

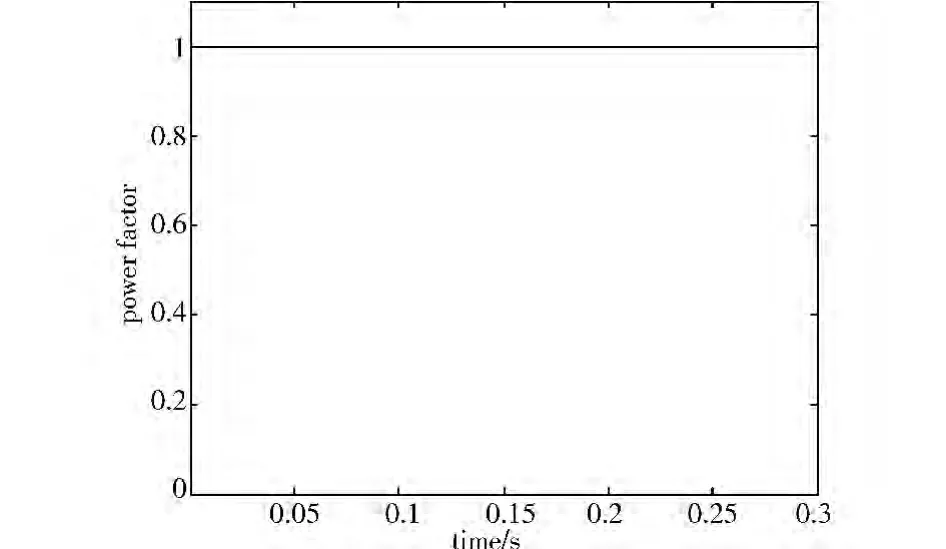
图9 微电网空载时的并网功率因数曲线

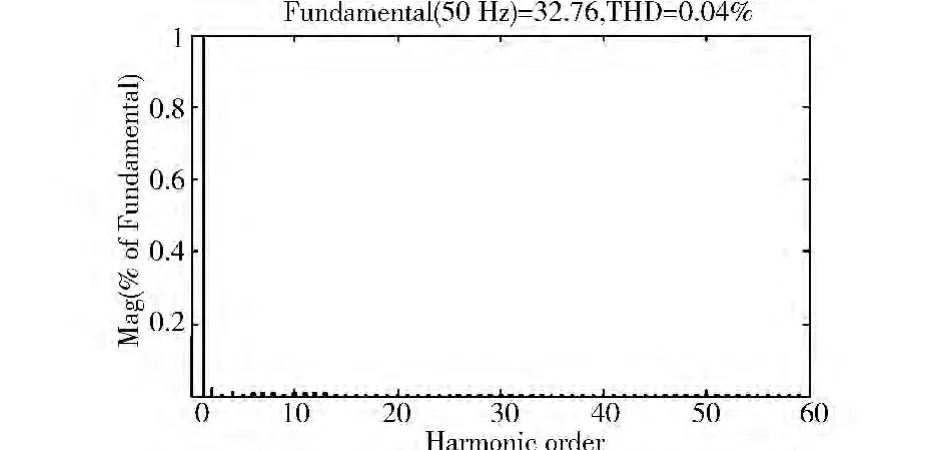
图10 微电网空载时的并网电流谐波分析图

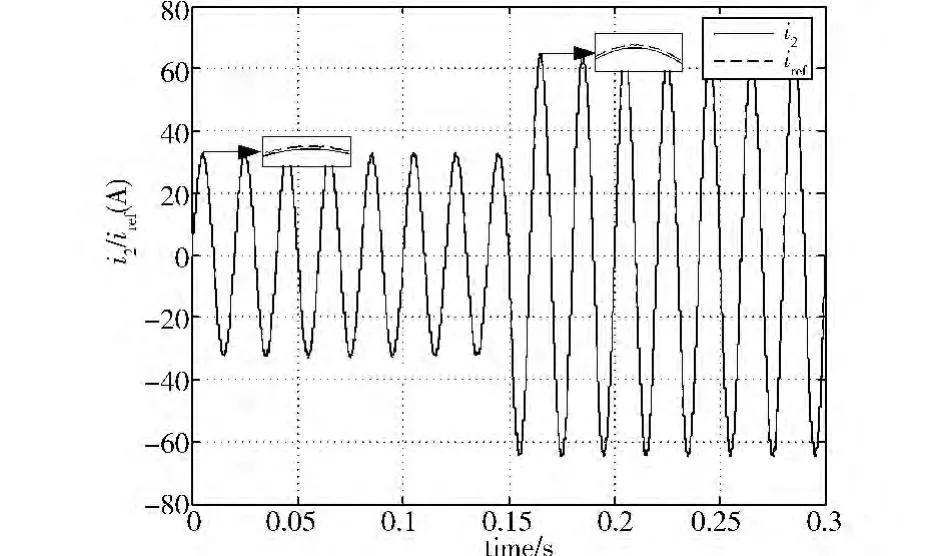
图11 微电网带负荷时的并网电流和参考电流波形图

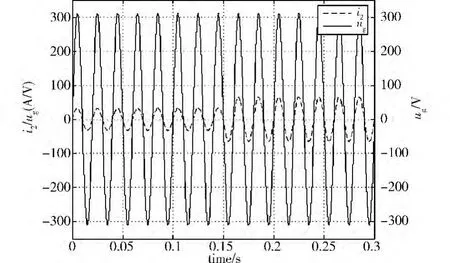
图12 微电网带负荷时的并网电流和大电网电压波形图

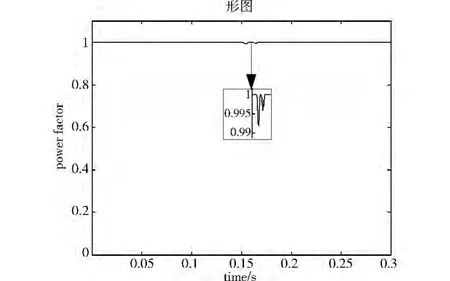
图13 微电网带负荷时的并网功率因数曲线

不足之处在于搭建的模型较为简单，微电网等效为一个直流电源，负荷简化为一个纯电阻负载。后续的研究重点是对模型进行改良，并引进其他控制理论(如模糊控制)对该控制策略进行改进。

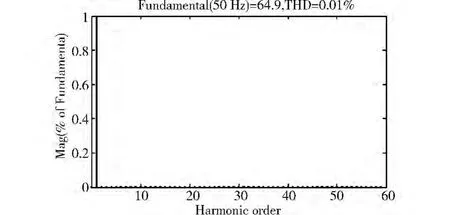
图14 微电网带负荷时的并网电流谐波分析

［1］ 吴卫民，刘松培，何远彬，等.单相LCL并网逆变器电流控制综述［J］.电源学报，2011，(2):51-58.

［2］ 王要强，吴凤江，孙力，等.带LCL输出滤波器的并网逆变器控制策略研究［J］.中国电机工程学报，2011，(12):34-39.

［3］ 赵炜，孙晓.光伏电站的数据采集系统［J］.新能源，2000，(9):31-34.

［4］ 鲍陈磊，阮新波，王学华，等.基于PI调节器和电容电流反馈有源阻尼的LCL型并网逆变器闭环参数设计［J］. 中国电机工程学报，2012，(25):133-142.

［5］ 黄挚雄，徐保友，沈玲菲，等.LCL并网逆变器新型电流双闭环控制策略研究［J］.电力系统保护与控制，2012，(17):1-5.

［6］ 曾正，杨欢，赵荣祥.LCL滤波并网逆变器的鲁棒控制［J］. 高电压技术，2011，(12):3143-3148.

［7］ 朱瑞林，韩金刚，汤天浩.并网逆变器LCL型滤波器的设计及有源补偿［J］.电源学报，2012，(3):43-47.