无损图像压缩编码方法及其比较
冉晓娟
(四川旅游学院信息技术,四川成都610000)
如今,信息早已成为一种重要的产品,其数量正以几何级数的速度迅速增长。随着多媒体技术与通讯技术的发展,人们对信息数据的存储与传输提出了更高的要求,尤其是具有庞大数据量的数字图像(其中往往存在着多种冗余信息)。如何快速有效地获取、存储并传输,对图像通信的发展至关重要。
在保证复原图像有较好质量的前提下,通过删除原始图像数据中的冗余信息以减少图像的数据量,提高存储效率,实现图像在网络中的快速传输与实时处理的手段。图像压缩技术正受到人们越来越多的关注。
图像压缩技术的研究至今已有60多年的历史,学者们提出并设计了多种实现图像压缩的方法。其中,根据压缩过程中有无信息的损失,可将图像压缩技术分为无损压缩和有损压缩[7]。顾名思义,无损压缩是指图像在复原过程中不会产生任何失真;但有损压缩则是通过损失图像信息细节而换取较高压缩比,此种压缩方法在复原过程中会对原图造成一定程度的失真,只能近似地恢复原图像。
1 图像压缩原理
在信息论中,信息量是如下定义的:对于某一个离散无记忆信源a,它产生的消息集合为aiYi=1,2,…,NY,假设每个消息ai出现的概率为P(ai),则所有消息出现的概率之和应为1,即由此,可推导出每个消息ai所携带的信息量为[1]:
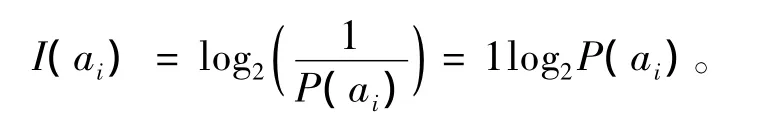
可见,一个消息出现的可能性越小,其携带的信息量反而越多,对信息的贡献量也越大。
若将信源所有信息量进行平均,则可以得到信源中每个消息的平均信息量,即信息的熵为:
根据香农第一定理——可变长无失真信源编码定理,对于熵为H的信号源,对其进行无失真编码所可能达到的最低比特数为H+ε。这里为任意小的正数,因此可能达到的最大压缩比为[2]:
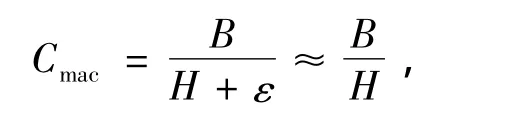
式中,B是原始图像的平均比特率,压缩比为[2]:

2 三种无损压缩方法的原理
受数据冗余度的理论限制,无损压缩一般只能获得2~5倍的压缩率。尽管如此,由于其还原后的文件可与原文件完全相同,可保证信息细节的不失真。因此,适用于压缩文本、程序和对细节十分敏感且不允许出现失真的一些特殊领域的图像数据。常用的无损压缩方法主要分为基于字典和基于统计两大类。
基于字典式的无损压缩,其生成文件中通常含有12至16位定长码。字典中每个定长码代表原数据中的一个特定序列;而基于统计式的无损压缩则是根据各个字符出现的概率,用变长码来代替各个字符,实现数据压缩。目前,常用的无损压缩方法有算术编码、香农-范诺编码、哈夫曼编码、游程编码和LZW编码等。本文仅针对后述三种无损图像压缩方法的原理进行研究与比较,以突出无损图像压缩编码方法在整个图像信息处理中的重要作用。
2.1 哈夫曼(Huffman)编码
哈夫曼编码是美国数据家Huffman为解决当年远距离通讯的数据传输的最优化问题,在1952年发明的一种基于统计的利用变长码来使冗余量达到最小的无损编码方法。信号源中字符出现的概率相差越大,Huffman编码效果越好。
哈夫曼编码算法的基本思路是利用最优二叉树进行编码,出现频率越高的值,其对应的二进制编码长度越短;反之,出现频率越低的值,其对应的二进制编码长度越长。因此,在产生哈夫曼编码的实际工作中需要对原始图像进行两次扫描。第一次扫描的目的是要精确地统计出原始图像中每个灰度值出现的概率;第二次扫描则是建立哈夫曼树并进行编码。由于需要建立二叉树并遍历二叉树生成编码,因此Huffman编码方式在数据压缩和还原速度方面都较慢,但由于其简单有效,因而得到广泛的应用。其操作步骤如下:(1)扫描原始图像,对其进行灰度值分布概率统计,得到N个信息符号的不同概率Pi(i=1,2…,N);(2)将N个信息符号按其概率值Pi递减的顺序进行排列;(3)将两个概率值最小的信号进行合并,形成一个新信号,设置新信号的概率值为此二信号的概率值之和,且概率个数减少为N-1个;(4)将新概率值放入集合后,重新按概率值递减顺序进行排列;(5)重复第3、4步,直到概率值相加为1时为止;(6)对生成二叉树的左右分支,按照统一规律进行二进制码元0,1赋值(如左分支代表0,右分支代表1);(7)从根结点开始到叶结点,将树枝上的值按顺序组成二进制值,生成Huffman编码。
2.2 游程编码(RLE)
数字图像中,每一扫描行中具有相同灰度值的相邻像素组成的序列称为一个游程,因此,可用灰度游程串来表示图像数据。游程编码技术(Run Length Encoding)正是利用了游程的特点,在对图像数据编码时,只存储每个游程的灰度值及组成该游程的相邻像素的个数,从而达到缩减重复出现的灰度值数量的目的,实现图像压缩。可见,当图像中含有少量灰度级,或者图像是由灰度相同或很多块颜色的大面积区域组成时,尤其是二值图像时,采用游程编码能获得效果最佳的压缩比。实际应用中,游程编码分为两大类:定长游程编码和变长游程编码,并且常常和其他编码方法结合使用。游程编码的基本步骤如下:(1)读入一副图像并对其进行转换,将其转换为二值图像;(2)对转换后的二值图像,按位进行扫描,判断是否值得压缩;(3)若第二步判定为真,则扫描图像每一行,并对相同灰度值的相邻像素进行计数统计,按照灰度值及像素个数进行统一编码,直至图像扫描结束。
2.3 LZW编码
LZW编码是在以色列人Lemple和Ziv共同提出的LZ压缩技术(即查找冗余字符并用较短代码代替冗余字符)基础上,经美国人Welch扩充而形成的一种先进的串表压缩方法,简称为LZW压缩方法,被广泛应用于图像压缩领域。其原理是让每个字符都与下个字符配成一个字符对,并为每个字符对设定一个数字。当相同字符对再次出现时,就用数字来替换,然后再将这个数字与下一个字符继续配对,生成的压缩文件只存储数字不存储字符对,从而大大提高了图像文件的压缩比。故采用LZW编码时,首先需要建立一个用以存储字符串及其对应数字代码的字符串表,然后把每一个首次出现的字符串放入字符串表中,并用一个与该字符串在字符串表中的位置有关的数字来代表此字符串,并将这个数字存入文件中;如果再次出现该字符串,则用代表它的数字来代替该字符串,并将数字存入字符串表中。
由此可见,字符串表是在压缩过程中动态生成的,因此当压缩结束后,可丢弃字符串表;同样,解压过程能根据压缩数据正确地重构字符串表,因而也不需存储字符串表。这样,就不需要占用额外的空间来存储字符串表,从而减少了压缩文件的大小。
3 三种无损压缩方法的分析比较
以上的三种无损压缩编码在一定程度上都实现了对图像数据的压缩,用尽可能少的信息量来实现数据的无损存储与传输,起到了很好的作用。但各种编码方法根据其适用对象又各具特点。
3.1 Huffman编码方法
根据前面的介绍可知,Huffman编码更适合于对概率分布不均匀的信源进行编码。它的不足之处主要体现在以下几个方面。
(1)必须精确地统计出原始文件中每个值的出现频率,如果没有这个精确统计,压缩的效果就会大打折扣,甚至根本达不到压缩的效果。由于哈夫曼编码要进行二次扫描,这样一来,对较大的文件进行编码时,频繁的磁盘读写访问必然会降低数据编码的速度,不利于网络实时压缩和传输。
(2)对位的增删敏感。哈夫曼编码将所有位合在一起不考虑字节分位,因此增加或者减少编码的位都会使译码结果面目全非。
(3)需要用额外的位保存和传输Huffman树,从而“浪费”掉一些存储位,把本已减少的数据量又增加了一些。如果文件比较大,这一点多余的数据所占比例很小,但如果压缩的文件本来就很小的话,增加的多余存储数据会明显影响压缩效果。
基于Huffman算法的这些缺陷,不少人提出了一些自适应算法。自适应算法不必等到全部数据输入完成才开始树的构造,可以根据后面输入的数据动态的对Huffman树进行调整。实际上,实用的Huffman树都是经过某种优化后的动态算法。
3.2 游程编码方法
作为压缩文件最简单的方法之一,游程编码简单直观、编码速度快,容易实现,对于具有长重复值的串的压缩尤其有效。常见的BMP和TIFF格式文件均采用RLE编码,另外视频文件AVI也将RLE作为其缺省压缩方式。但是对于灰度图及颜色丰富的彩色图像进行压缩时,单纯使用RLE压缩算法无法取得很好的效果。
3.3 LZW编码方法
LZW编码原理的一个重要特征是,代码不仅仅能取代一串同值的数据,也能够代替一串不同值的数据。在图像数据中若有某些不同值的数据经常重复出现,也可编写一个代码来取代这些数据串。因此,LZW压缩编码很适合压缩有大块相同色彩或重复颜色图案的点阵图,相同的色块越多,压缩比也越大。LZW压缩技术比其他大多数压缩技术都复杂,压缩效率也较高。它一般包含在TIFF和GIF文件格式中:在TIFF中,LZW压缩只是一个选项,可执行可不执行;而在GIF文件格式中,它作为缺省方式存在。此外,LZW编码是可逆的。
4 结束语
随着通信技术和多媒体技术的飞速发展,数字图像已成为人类获取和传递信息的重要手段之一。日益精细的图像中包含了越来越丰富且巨大的数据量,这对图像的高效存储与快速传输提出了更高的要求,图像压缩技术恰好为解决这一难题提供了强有力的支撑。本文针对三种常用无损压缩编码方法的原理及操作步骤进行研究、分析与比较,介绍了各自的特点及不足。由此可见,丰富的图像数据单纯依靠某一种压缩算法,都无法得到理想的压缩效果。因此,在选择具体算法的过程中,应根据实际图像的特点,选择最合适的压缩算法,有时往往还不只一种方法,才能获得最好的压缩效果。此外,由于受数据冗余度的理论限制,如果直接对图像采用无损压缩编码,得到的压缩比不可能有很大的提高。因此,可考虑先对图像采用基于小波变换的图像去噪算法来减少其中的冗余信息量,然后再采用上述无损压缩算法对图像进行压缩的处理方案。如今,在数字图像压缩领域,人们除了要求高压缩比以外,还越来越重视图像压缩的可靠性——要求图像具有完全的可复原性和高度的保真效果,以及压缩的实时性。因此,迫切需要对高效的无损压缩算法进行深入的研究。
[1] 夏良正.数字图像处理(修订版).南京:东南大学出版社,2002.
[2] 艾海舟.数字图像处理(多媒体课件)(第二版)[DB/OL].http://media.cs.tsinghua.edu.cn/~ ahz/digitalimageprocess/chapter14/chapt14_ahz.htm,2001-07-19/2014-11-01.
[3] 汪炼,韩震宇.无损图像压缩技术[J].实用测试技术,2002,(5):33-34.
[4] W K普拉特.数字图像处理学[M].北京:科学出版社,1984.
[5] 陈衍仪.图像压缩的分形理论和方法[M].北京:国防工业出版社,1997.
[6] 黄贤武.数字图像处理与压缩编码技术[M].四川:电子科技大学出版社,2000.
[7] 冯希.几种图像无损压缩与编码方法的比较研究[D].北京:中国科学院研究生院,2008.
[8] 籍俊伟.无损图像压缩技术的研究与应用[D].北京:北京化工大学,2004.
[9] 张玉彬.LZW数据压缩算法的原理分析[EB/OL].http://www.cnblogs.com/jillzhang/archive/2006/11/06/551298.html,2006-11-06/2014-11-01.

