基于GARCH模型的金融风险拟合分析

司训练 张旭峰 高 蒙

(1．西安石油大学 油气资源经济与管理研究中心，陕西西安710065;2．长安大学 理学院，陕西 西安710056)

0 引言

由于金融资产的预期收益总伴随着一定的风险，尤其是20世纪90年代中期以来，国际金融市场上接二连三地发生金融风波，使学者们从金融风险理论的研究逐渐转向对金融风险量化的研究，以期寻求能够准确反映股票价格波动特征与规律的方法。现实中，经常看到一些投资者没有采取合适的风险规避机制，盲目地进行投资，不仅丧失了盈利的最佳时机，而且也使自己承担了额外的投资风险。可以说，我国对于金融理论和实践的研究远远落后于股市的发展。这些都造成了我国股市波动幅度和风险显著高于国外成熟市场的问题，尤其是异常波动和超常波动频繁出现。因此充分借鉴世界先进的风险管理模式，探索我国金融市场资产价格的波动特征，建立适合我国金融市场的波动模型具有重要意义。

1 相关文献综述

有关金融风险度量的理论最早是Markowitz提出的用收益方差度量证券投资的风险，该方法虽简便易行、适应性强，但其假设相对严格，某些情况下不能很好地刻画金融风险的变化［1］77-91。同年，罗伊提出“安全第一法则”，即利用某个预设的风险水平的概率水平应高于其投资价值来调整投资风险，从而进一步发展了风险测度理论。该方法虽简单直观，使用范围广泛，但是其对产品类型的依赖性高，具有不稳定性和相对性，这就有可能造成对金融风险拟合分析的失真。之后，Engle提出的ARCH模型描述了金融时间序列的“异方差性”和波动“群集性”［2］987-1007。Bollerslev将ARCH模型的阶数推广到无穷，得出了广义自回归条件异方差模型(GARCH)模型，由此各种各样的GARCH模型层出不穷，由此形成了ARCH类模型［3］5-59。GARCH模型能够很好地度量金融时间序列数据的波动性，对金融风险的拟合效果更优，在此基础上，G-30集团又提出了风险价值法，J．PMorgan提出了用于计算VaR的RiskMetrics风险度量模型［4］3-8。VaR方法的优点是可以度量不同金融工具构成的复杂证券组合和不同部门的总体市场风险，并且概念简单，易于理解，但是VaR方法不适用于市场发生极端情况下的风险度量，不能反映投资组合的风险分散化效应。

近年来，金融计量经济学的研究最为突出的是学者们广泛地考虑了金融风险度量中的波动性，而最能刻画波动性的表性的模型就是ARCH类模型，因为它能刻画收益序列的波动群集性和异方差性［2］987-1007，因而在近十几年里被广泛地应用于金融理论中的规律描述和金融市场的预测和决策。ARCH模型是获得2003年诺贝尔经济学奖的计量经济学成果之一，被认为是最集中反映了方差变化特点而被广泛应用于金融数据时间序列分析的模型，目前在所有的波动率模型中，ARCH类模型无论从理论研究的深度还是从实证运用的广泛性来说都是独一无二的。

2 理论模型简介

股票指数是一种金融时间序列，其分布一般不服从正态分布［5］10-13。Engle提出股市波动的聚集性和持续性的ARCH模型，其持续方差和处理厚尾的能力，能够很好地描述股票价格的波动特征［6］610-617。为了达到更好的拟合效果，一般就会使误差项的滞后阶数变得更大，但这样会增加待估参数个数，也会降低参数估计效率。GARCH模型相对于ARCH模型来说，不仅提高了反映波动率的准确性，而且减少了待估参数的个数。Bollerslev给ARCH模型中的条件异方差ht加入了自回归部分，即:

上面的模型是 GARCH(p，q)形式，以GARCH(1，1)为例［7］250-253，可得到:

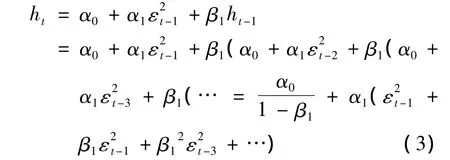
GARCH模型中ht对过去的误差性平方具有无限记忆性，这与金融市场中的时间序列数据特性更加吻合，而且对很多现象的描述也比ARCH模型简洁。

利用条件方差表示预期收益的模型被称为ARCH-M模型，该模型是在1987年由Engle、Lilien、Robins引入的，其表达式为

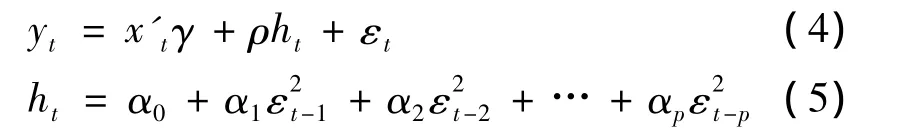
其中:参数ρ是用于衡量观测到的预期风险波动ht对yt的影响程度，它代表了收益和风险之间的一种权衡。

若把ht看成是一个类似(2)的GARCH(p，q)过程，则条件方差方程就能够写成

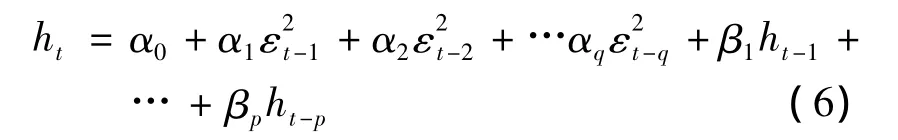
式(4)和式(5)被称为GARCH-M模型。

本文运用GARCH模型和GARCH-M模型的参数估计方法和相关检验理论，基于SAS软件对上证综指建立相应的波动模型，来拟合金融投资风险的波动情况。

3 实证分析

3．1 金融数据的统计描述

本文选取2002年5月27日至2012年5月3日上海证券交易所共2 413个日收盘指数作为计算值，采用SAS软件对上海股市的发展变化情况进行分析［8］35-483。

设t时刻的收盘价记为pt，t-1时刻到t时刻的投资收益率可定义为:

当采用复利计算投资收益时，则日收益率为对数收益:

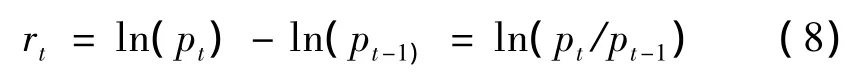
这样定义的原因是:在一个投资期间内，如果按m次复利计算，则有:

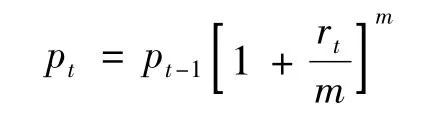
在对上海证券综合指数(以下简称上证综指)对数日收益率进行统计分析之前，首先介绍一下偏度与峰度的概念。偏度是指统计数据分布的偏斜方向和程度，它是统计数据分布非对称程度的数字特征，它是表征概率分布密度曲线相对于平均值不对称程度的特征数。峰度又称峰态系数，表征概率分布曲线在平均值处峰值高低的特征数;峰度反映了尾部的厚度。下面我们利用SAS软件统计上证综指对数收益的基本情况，详见表1所示。根据表1进行分析。

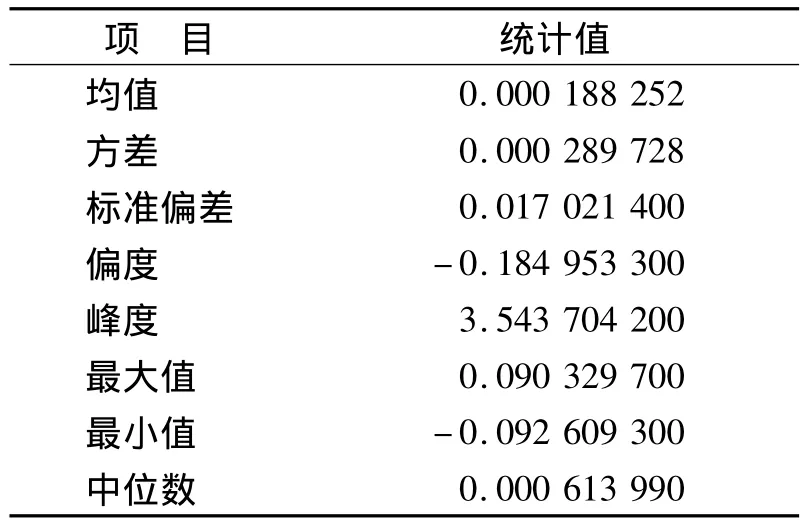
表1 上证综指对数日收益情况

(1)对数收益率均值的分析:样本对数收益率均值为0．000 188 252，说明投资者如果一开始就进行投资，能够得到一个较好的正收益，适用于长线投资。

(2)偏度与峰度的分析:上证综指的收益率偏度为负值，说明其分布没有长的右拖尾。这说明有很多游离在左侧的数据点，均值由于受到这些数据的影响将偏向左侧，所以大多数投资者很容易感觉到自己的收益率比平均水平要高。峰度为3．543 704 2 ＞3，说明上证综指的收益率分布尾巴要比正态分布厚，其分布密度曲线在距离均值较远的地方位于正态分布曲线的上方，这说明上证综指的对数收益率是不服从正态分布的。由于存在大幅偏离均值的异常值，且异常值成群出现，这就造成了收益率的概率分布呈现尖峰厚尾的现象。因为，股市的波动具有“丛集性”，即大波动跟随大波动，小波动跟随小波动。波动“丛集性”的存在说明过去收益的波动影响未来收益的波动，详见图1、图2、图3所示。

图1 收益时间序列

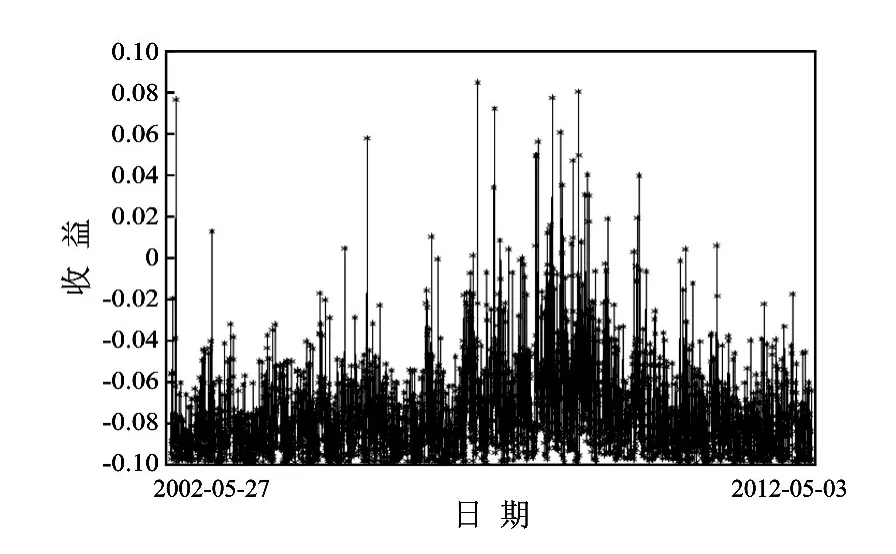
图2 绝对收益时间序列

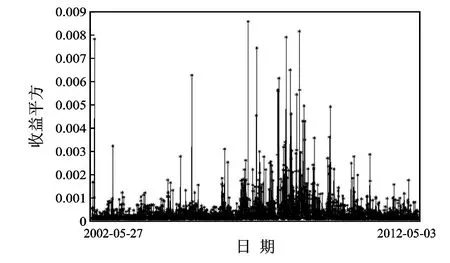
图3 平方收益时间序列

3．2 序列相关性和异方差性检验

相关性检验结果如表2所示。

表2 相关性检验

由表2可知，由于DW统计量的值1．986 0非常接近2，说明随机误差序列一阶不相关。而且Pr＜ DW对应的概率p值为0．357 4，大于0．05，说明随机误差序列并不是一阶正相关;而且Pr＞DW对应的概率p值为0．642 6，大于0．05，说明随机误差序列也不是一阶负相关。

异方差性检验结果如表3所示。

表3中，Q表示Q检验法的检验统计量，LM表示LM检验法的检验统计量，Pr＞Q和Pr＞LM分别表示该假设检验的概率p值。由表3可知，对上证综指自回归后的残差序列的Q检验和LM检验，滞后12阶的概率p值全都远远小于0．05的显著水平，拒绝原假设，即:残差项序列式存在显著的ARCH效应，上证综指的确存在异方差。

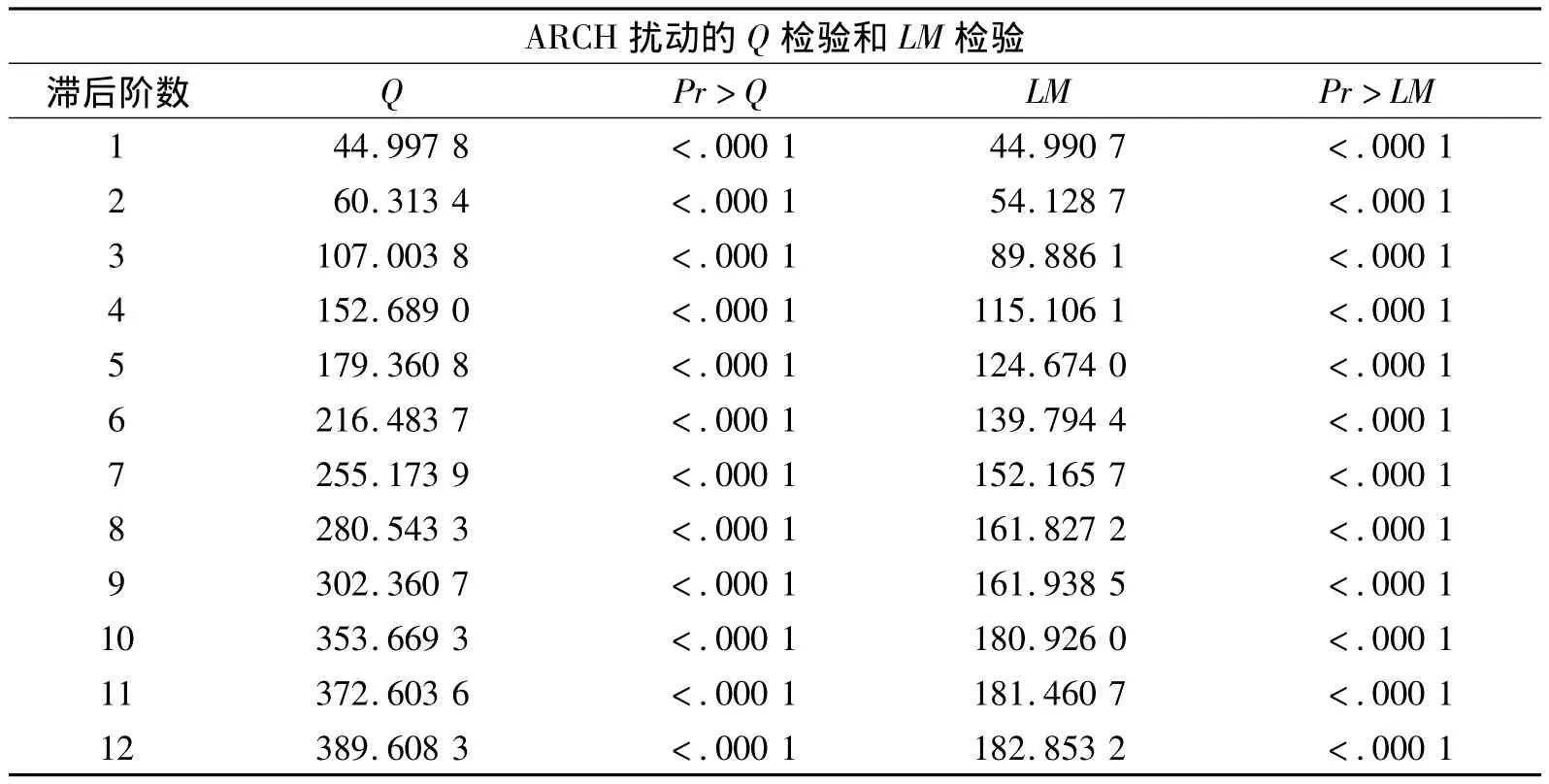
表3 异方差性检验

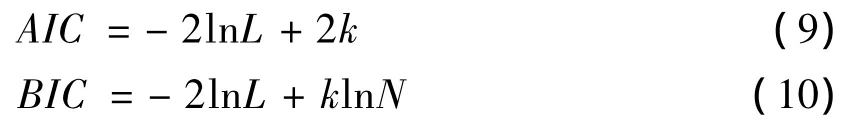
3．3 模型阶数的选择

时间序列定阶问题中常用的方法有AIC(Akaike Information Criterion)信息准则和Schwar的BIC信息准则［9］72。AIC和BIC的定义如下:

其中，k为被估参数的个数，N为观测个数，ln(L)为对数似然函数。

AIC由对数似然和参数个数决定，对数似然越小，模型拟合效果越好，模型中包含的参数越少越好用。AIC准则建议，在一组可选模型中，选择使得AIC最小的模型。BIC在AIC的基础上，考虑了样本容量对模型选择的影响，BIC准则也是选择使得BIC最小的模型。

利用 SAS软件，对 GARCH(p，q)模型和GARCH-M(p，q)模型拟合对数日收益，并计算相应的AIC和BIC值，详见表4所示。

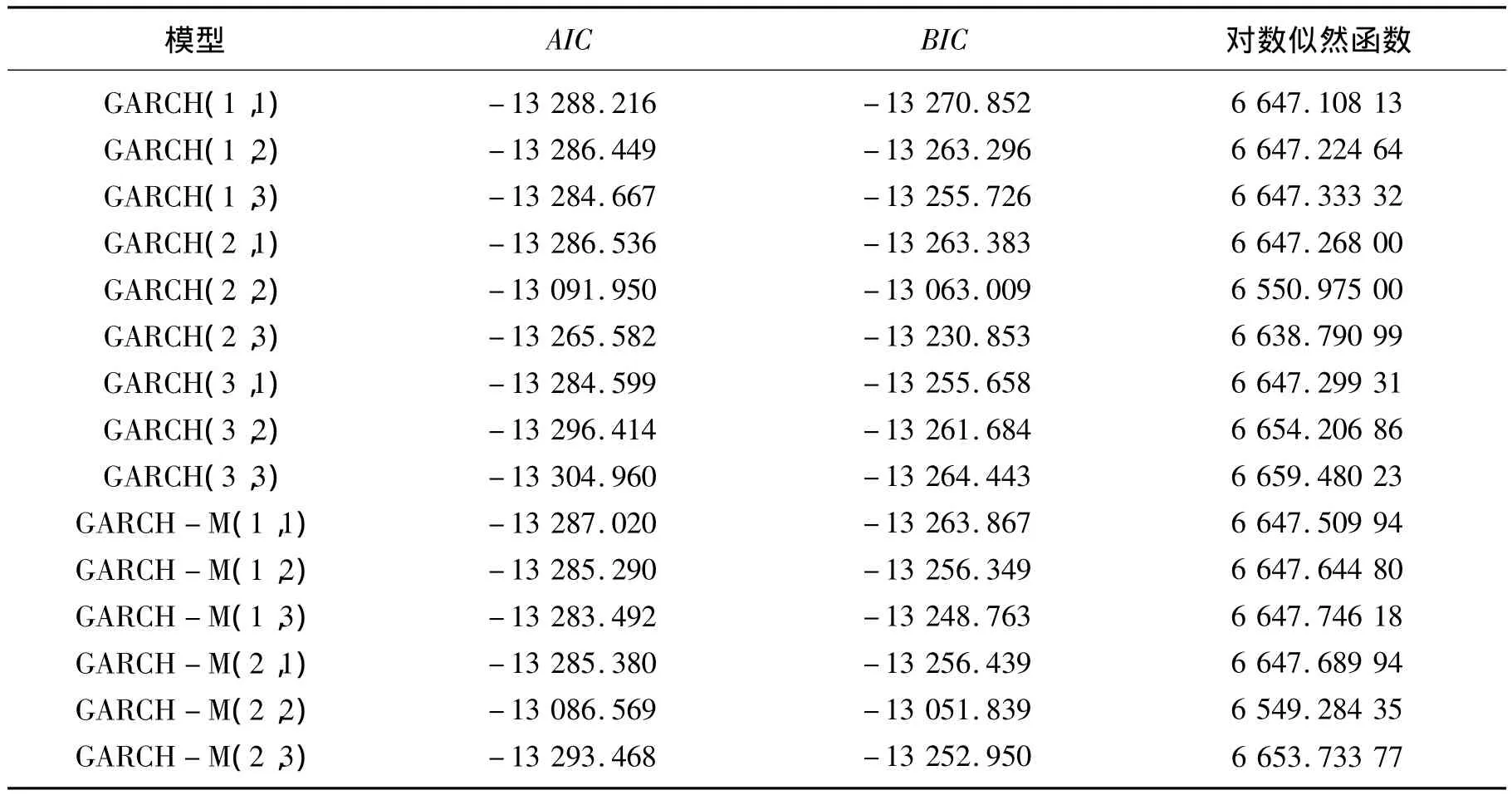
表4 各种模型的AIC、BIC和对数似然函数值

由表4可知，模型GARCH(1，1)的AIC值和BIC值最小，因而最佳的GARCH(p，q)模型应为GARCH(1，1)模型。同样，最佳的 GARCH-M(p，q)模型应为 GARCH-M(1，1)模型。

3．4 建立模型

根据以上分析可知，最佳模型应为GARCH(1，1)和GARCH-M(1，1)。下面我们分别给出两模型的参数估计值，如表5、表6所示。

表5 GARCH(1，1)模型的参数估计

表6 GARCH-M(1，1)模型的参数估计

由表 5 可知:α0=0．000 002 841 3，α1=0．062 9，β1=0．928 1，从而GARCH1，1 模型的具体表达式为:

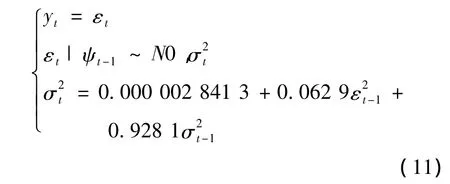
由表 6 可知:α0=0．000 002 842 2，α1=0．062 9，β1=0．928 1，γ =0．017 7，从而GARCH-M(1，1)模型的具体表达式为:

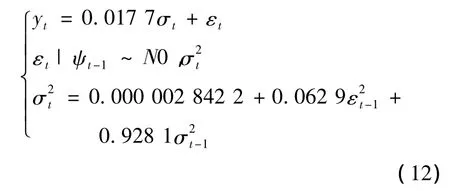
在GARCH-M(p，q)模型中，GARCH-M(1，1)对数据的拟合效果最好，在 GARCH(p，q)模型中，GARCH(1，1)的效果最好。GARCH(1，1)又比 GARCH-M(1，1)的拟合效果好，其原因:一是 GARCH(1，1)的 AIC和 BIC较 GARCH-M(1，1)小。二是GARCH(1，1)的参数估计表中概率p值全小于显著性水平0．05，说明各参数都显著，而 GARCH-M(1，1)的参数估计中DELTA对应的概率p值为0．331 3，大于显著性水平0．05，说明均值方程中σt的系数并不显著。

4 结语

根据本文对上证综指对数日收益率的实证分析，可得出以下结果。

(1)对数日收益序列存在显著的条件异方差和波动“丛集性”。也就是说，上证综指对数日收益的波动随时间的变化而变化，而且经常在某一时刻中连续出现偏高或偏低的情况。

(2)通过比较 AIC和 BIC信息准则，得到GARCH(1，1)和 GARCH-M(1，1)分别是最好的GARCH模型和GARCH-M模型，而且GARCH(1，1)模型比GARCH-M(1，1)模型对数据的拟合效果更好。

(3)GARCH模型和GARCH-M模型除常数项外的系数之和为0．991，接近于1，说明现时刻的波动对未来波动的影响时间较长，有明显的波动持续特征。若模型中系数之和小于1，说明模型具有可预测性，收益率条件方差序列是平稳的。在此，管理层制定实施相关政策时，应该准确地预测市场消化政策的能力，否则外部冲击对股市的影响将是长期的，因此，把握好政策调节市场的力度是非常重要的。

根据拟合波动性模型可知，我国股市风险较大，“羊群”效应显著，且投资者投机色彩浓厚。需要指出的是，我国股市的波动主要是由管理当局的政策干预造成的。因此，管理者对市场调控时应从长远的角度考虑，把握好政策的调整力度。目前我国股票市场各方面还不够规范，尤其是信息的提前泄露问题。当一条可能引起股价波动的信息尚未完全到达市场时，已有相当一部分人从各种途径获知该信息并做出了反应。这样，当信息正式到达市场时，市场已将其基本消化，价格的波动性随时间已缓慢释放完毕，从而不会发生预想程度的波动。

［1］Markowitz H．Portfolio selection［J］．Journal of Finance，1952(7)．

［2］Engle R F．Autoregressive Conditional Heteroscedasticity with Estimates of the Variance ofUnited Kingdom Inflation［J］．Econometrica，1982(4)．

［3］Bollerslev T，Chou R Y，Kroner K F．ARCH Modeling in Finance:A review of the theory and empirical evidence［J］．Journal of Econometrics，1992(1)．

［4］秦国平．基于VaR的我国商业银行市场风险计量［D］．南昌:江西财经大学，2010．

［5］ 夏师．上证指数收益率的统计分析［J］．中国证券期货，2009(11)．

［6］ 童恒庆．理论计量经济学［M］．北京:科学出版社，2005．

［7］ 林博．基于GARCH模型的VaR方法在上证市场中的应用［J］．时代金融，2013(9)．

［8］朱世武．S A S编程技术与金融数据处理［M］．北京:清华大学出版社，2003．

［9］高铁梅，王金明，梁云芳，等．计量经济分析方法与建模:EViews应用及实例［M］．北京:清华大学出版社，2009．