失谐耦合摆运动规律的研究

陈 伟，刘 明，葛帅良，刘 芬，王爱芳

(山东大学，山东 威海 264209)

耦合摆是物理学中的一个重要的学习模型，有助于加深学生对耦合振动的认识和理解，也是大学物理实验中一个重要的实验项目。但是，在实际使用耦合摆时，因为双摆的质量差异、弹簧两端点的高度位置差异和弹簧的自然长度与双摆间的距离差异等因素的存在，使得通常情况下耦合双摆容易存在误差。因此有必要考虑物理量的失调对双摆运动规律的调制。钱斌等人对不同质量的耦合摆运动规律进行了讨论［1-2］，路峻岭等人对起耦合作用的弹簧进行了改进［3］，本文主要讨论倾斜的弹簧对双摆运动规律的影响。

1 倾斜的弹簧对耦合摆角频率的影响

1.1 耦合摆振动系统的运动学分析

图1 倾斜的弹簧作用下的失谐摆

图1为一个简单失谐耦合摆系统，该系统由一劲度系数为k的弹簧弱耦合起来，两个摆的质量均为m，摆线总长均为L，其中，右摆耦合长度由l变为l(1－ε)，ε反映了弹簧的倾斜情况，称为倾斜因子，取向上为正。略去阻尼影响，取摆偏离平衡位置的角度分别为θ1、θ2，并以偏右为其正方向，取悬挂点水平线为零势能线，则有

耦合摆动能:

耦合摆的势能为重力势能V1和弹性势能V2之和，即 V=V1+V2。其中，重力势能 V1=－mgL cosθ1－ mgL cosθ2，由于 θ1、θ2很小，即sinθ1≈θ1，cosθ1≈1;sinθ2≈ θ2，cosθ2≈ 1，故有 V1≈－2mgL。

弹性势能:

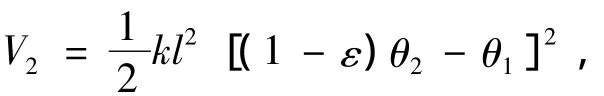
故双摆总势能:

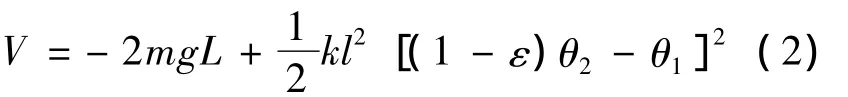
由公式(1)－(2)可得系统的拉格朗日函数:

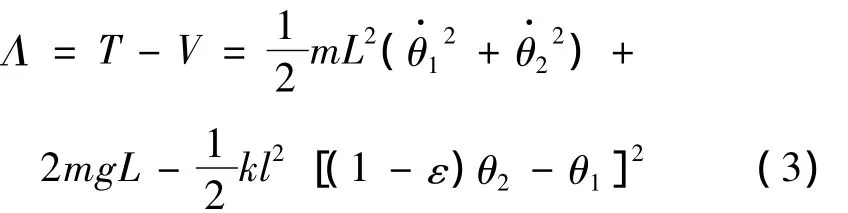
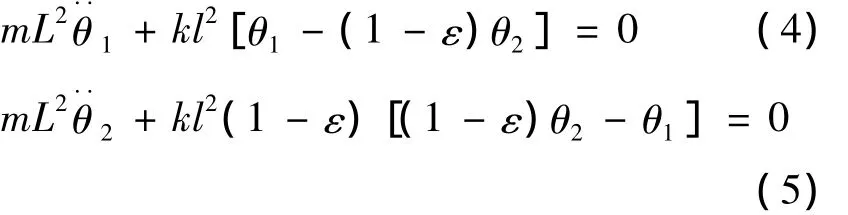
由(4)和(5)式，知道:当ε=0时，由于对称性，则左、右两摆的振动状态仅由初始条件(同相位运动或者反相位运动)决定，此时是谐振状态的耦合摆;当ε≠0时，左、右两摆的振动状态由初始条件和ε大小共同决定，并且随着ε的变化，左、右两摆的振动频率ω1和ω2改变幅值不同，此时耦合摆处于失谐状态。

1.2 失谐耦合摆的数值模拟

下面用Fortran编程模拟双失谐耦合摆的运动规律。在程序中取劲度系数k=1.45 N/m，L=0.6 m，l=0.25 m，m=0.75 kg;倾斜因子 ε 取值范围为 －2.5/25 ～ 2.5/25 cm，步长为0.5/25cm;取时间间隔τ=0.01 s，把30 s离散为3000个时间点。取ε为外生变量，绘出两个摆瞬时角频率之差ω1－ω2与时间t的关系曲线。图2(a)和(b)中每条曲线代表不同的ε值对ω1－ω2的影响。(a)中ε取值范围为正值［0，2.5/50］，(b)中ε取值范围为负值［－2.5/50，0］。随着 |ε|值的增大，ω1－ω2的值逐渐增大，即耦合摆的失谐程度增强;当ε=0时，ω1－ω2=0不随时间变化，说明此时为谐振状态的耦合摆。

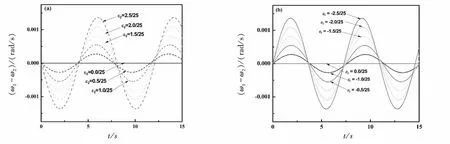
图2 双摆的简正频率差值随时间t的变化关系

1.3 实验结果

为进一步确定失谐耦合摆在不同倾斜弹簧下对耦合摆的作用，实验测量了双摆的振动周期。在实验中，令左、右摆反向摆动，且初始角θ10=－θ20＞0，初始角速度ω10=ω20=0，探究不同倾斜因子对两摆振动周期的影响。左、右摆的平均角速度ω1和ω2随弹簧倾斜因子ε的变化曲线见图3。

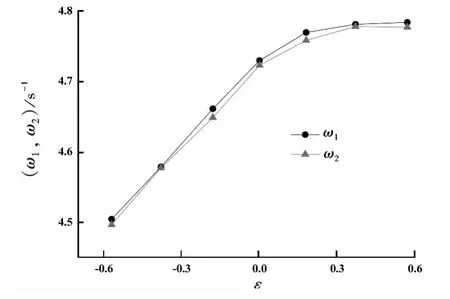
图3 反向振动情况下倾斜因子e对双摆角频率ω1和ω2的影响

随着倾斜因子的增大，右摆上的弹簧自下向上移动，双摆的平均振动角速度逐渐增大。而且平均角速度的增幅随着ε的增大而减小，当ε＜0时，即弹簧倾角向下的时候，对角频率的影响较大。

2 弹簧的等效平衡

上述所讨论的是失谐的一个简化模型，要想使得双摆再次谐振，必须添加另外的装置使系统重新谐振。在本文中，尝试增加另外一根性能完全一致的弹簧2抵消此失谐对耦合振动的影响，鉴于弹簧的倾斜度对角频率的影响是非线性的，故不能简单地确定弹簧2的位置，下面将对双倾斜弹簧作用的双摆进行运动分析。

2.1 耦合摆振动系统的运动学分析

图4所示为一个连接两根弹簧的耦合双摆系统，设该系统由两个相同的劲度系数为k的弹簧弱耦合起来，两个摆的质量均为m，摆长均为L，则右摆耦合长度由 l分别变为 l(1－ε2)和l(1－ε1)，取向上为正。取摆偏离平衡位置的角度分别为θ1、θ2，并以偏右为其正方向，悬挂点水平线为零势能线，由拉格朗日方法同理可得左、右摆的运动方程为:

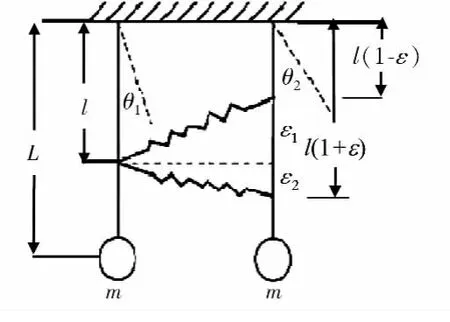
图4 双弹簧作用下的耦合双摆

由(6)和(7)两式，当ε1= ε2=0时，两弹簧的作用可以等效为一根水平弹簧的作用效果，此时为谐振状态的耦合摆;当ε1=ε2≠0时，左、右两摆的振动状态由初始条件和双弹簧的倾斜因子的大小共同决定，此时左、右两摆的角频率不相同;当ε1≠ε2时，随着ε1和ε2的变化，左、右两摆的振动角频率将有更复杂的变化。

2.2 双弹簧耦合摆的数值模拟

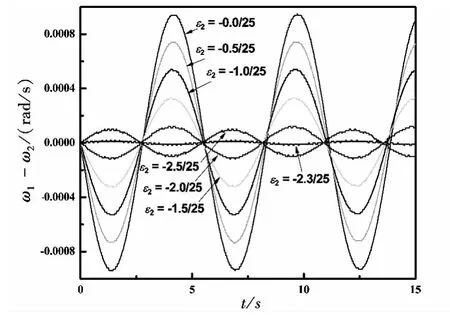
图5 不同ε2值作用下的双摆振动角频率差值ε1=2.5/25 保持不变

用Fortran编程求解双弹簧作用下耦合摆的振动角频率随时间的变化，在程序中劲度系数k、摆长L、耦合长度l、摆的质量m的取值仍然取 1.1中的数值;倾斜因子 ε1取定为 2.5/25，ε2的取值为 － 2.5/25 ～ 0.0/25，计算步长为0.5/25;时间间隔 τ =0.01 s，把30 s离散为3000个时间点。固定ε1，取ε2为外生变量，计算得出角频率差值ω1－ω2随时间的变化关系如图5所示，图中每条曲线代表不同的ε2对ω1－ ω2的影响。ε2的取值范围为［－2.5/50，0］。根据图5中模拟的结果也能看出倾斜因子的改变对双摆振动角频率的影响是非线性的。由图可知，当ε2取 －2.3/25时，ω1－ ω2=0且随时间的变化最小，此时可以视为谐振的耦合摆。并且由谐振时，ε2= －2.3/25 ＜ ε1可知，弹簧1的倾斜角大于弹簧2的倾斜角，所以相同大小的倾斜因子，取负值时对角频率的改变量较取正值时大，与1.3中的实验结论相吻合。

2.3 实验结果

根据上文模拟数值的结果，可以得出，要想使得双倾斜弹簧作用的耦合摆达到标准耦合摆的振动效果，两个弹簧的倾斜因子之间需要满足条件－ε1＜0。在接下来的实验中，令双摆由相同的初始角度(θ10=θ20)摆下，初始角速度ω10=ω20=0，固定左耦合长度l和ε1不变，将ε2的值由零逐渐增大，测量两摆振动规律。图6给出了左右摆的振动角频率之差ω2－ω1随二者的倾斜因子之差ε2－ε1变化的关系，由结果容易发现当两弹簧倾斜因子相同，即ε2－ε1=0时，左右摆并非谐振耦合摆，只有当－ε1＜0时，双摆的振动角频率才可能相等。因此，当弹簧2与弹簧1对称偏上的位置时，ε2补偿因ε1的存在而引起的耦合摆的失调是可以实现的。此时，两根弹簧的作用效果等效于一根水平弹簧的作用效果。［7-8］

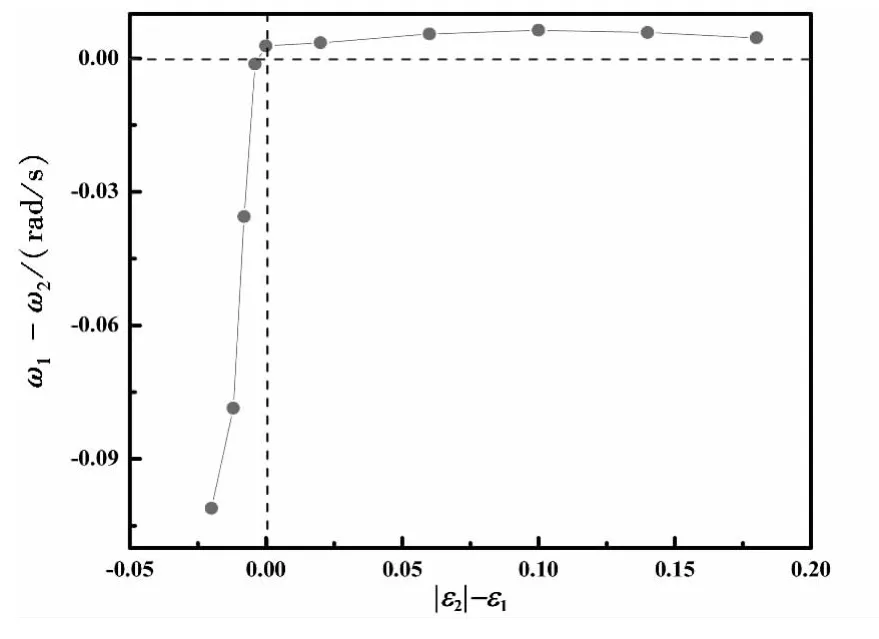
图6 双弹簧连接时倾斜因子之差ε1－ε2对ω2－ω1的影响

3 结 论

本文利用拉格朗日方法、数值模拟和实验测量研究了倾斜弹簧作用下的耦合摆的运动规律，当双摆之间连接一根倾斜弹簧时，左右摆的角频率ω1和ω2随倾斜因子的变化并非以相同幅值改变，并且当弹簧倾角向下时较倾角向上时对振动角频率的影响大。对于双倾斜弹簧作用下的双摆，可以通过采取补偿的方法调节耦合摆的振动，并且双弹簧倾斜因子在满足一定的条件时，能够实现将非谐振双摆调至谐振状态。在实际应用中，可以借助双根弹簧共同调节和稳定耦合振动仪表，为提高测量精度提供新的可调节手段。

［1］钱斌.小球质量对失调耦合摆的影响［J］.常熟理工学院学报:自然科学版，2007，21(8):31-34.

［2］隗功民.弹簧质量对耦合摆小振动角频率的影响［J］.大学物理，1997，16(7):19-27.

［3］路峻岭，汪荣宝.对耦合摆实验中耦合弹簧的改进［J］.大学物理，2005，25(8):36-37.

［4］龚善初.失调耦合摆振动分析［J］.大学物理，2005，24(8):21-24.

［5］舒幼生，胡望雨，陈秉乾.物理学难题集萃［M］.北京:高等教育出版社，1999:299.

［6］陈世民.理论力学简明教程［M］.北京:高等教育出版社，2001:184-189.

［7］朱华泽.用波尔振动仪研究受迫振动特性［J］.大学物理实验，2011，24(3):57-59.

［8］王颖.用Audition软件辅助测量弹簧振子振动周期［J］.大学物理实验，2011，24(3):73-75.