基于合同储备的军地物资联储经济分析

龙绵伟，荀 烨，陈新民

(1.军事交通学院 军事物流系，天津300161;2.军事交通学院 研究生管理大队，天津300161)

依托国家、地方和社会资源，实现军民结合的战备物资储备，是深化军队战备物资储备改革的发展趋势［1］。合同储备是继军队自主式实物储备和“以厂代储”模式之后出现的又一种新型储备模式，是军民融合式物资储备模式的重要组成部分［2］。本文运用经济学有关理论方法，分析了基于合同储备的军地联储模式在经济上的可行性及其应当达到的临界条件。

1 合同储备的概念及分类

合同储备是指由军队与地方单位签订合同，军队在平时按合同约定给予地方代储单位或生产企业一定的经济补贴，地方代储单位或生产企业根据合同在平时履行代储责任或保留一定的生产能力，保证在约定的时限内完成物资的筹措或生产并以市价供应军队或政府［3］。根据战备物资在企业中的存在形态，战备物资合同储备可以分为无产权实物合同储备和生产能力合同储备［2-3］。军队无产权实物储备是军队根据市场通行规则给地方单位支付一定数额的定金，军队没有物资的所有权而只拥有物资的优先使用权，地方代储单位以实物的形式按军队要求完成物资储备，当军队需要时以市价供应军队。生产能力合同储备是为保证紧急状态下物资供应，在军队提供适量补贴的前提下，由生产相似物品的单位根据军队需要保有一定的生产能力储备，如人员、场地、生产线、原料等，确保在军队提出需求后能在短时间内完成转产，并按预定的生产速度生产储备物资，以市价供应军队。

2 基于合同储备的军地联储模型构建

2.1 问题分析

基于合同储备的军地联储有军队与合同企业实物储备，军队实物储备与合同企业生产能力储备，军队与合同企业实物、生产能力储备3 种形式。本文从军队与合同企业实物、生产能力储备这种最复杂的情况出发进行分析研究。在这种储备模式下，物资供应链由合同企业和军队组成。军队和合同企业共同进行部分物资实物储备，同时，军队以生产能力补贴的方式使企业保有一定物资生产能力储备。军队储备、合同企业实物储备和合同企业生产能力储备，除了储备成本不同之外，其对物资需求保障能力也是不同的;因此，区别于单一储备主体的储备模式，在该储备模式下，引入保障能力参数，综合保障能力和储备成本2 方面因素做出物资储备量的决策。

2.2 问题假设

(1)假设军队储备和合同企业实物储备、生产能力储备的成本结构、收益函数及物资需求分布函数是共同知识。

(2)假设军队及合同企业的实物储备全部用于满足物资需求，合同企业根据实物储备不足部分进行生产。也就是说，期末军队及合同企业的实物储备物资库存量为零。

(3)军队只向合同企业支付已使用物资的采购价款。

令D1为物资总储备量，λ1D1为军队储备量，λ2D1为合同企业实物储备量，(1-λ1-λ2)D1为合同企业生产能力储备量。

令P为单位物资价格，由外部市场环境决定;C1为合同企业单位物资生产成本(包括原材料购买成本、生产费用、运输费用等);C2为军队单位物资库存成本;C'2为合同企业单位物资库存成本;g为合同企业物资储备不足时的单位惩罚成本;C3为合同企业实物储备补贴，C3=a+αλ2D1λ2D1。其中:a为实物储备固定补贴;α 为实物储备补贴浮动系数，α 的取值为储备量λ2D1的分段函数。

C4为物资生产能力储备补贴，C4=b+β(1-λ1-λ2)D1(1-λ1-λ2)D1。其中:b为生产能力储备固定补贴;β 为生产能力储备补贴浮动系数，β的取值为物资生产能力储备量(1-λ1-λ2)D1的分段函数。

C'4为合同企业保有生产能力储备的成本，C'4=c+ε(1-λ1-λ2)D1。其中:c为合同企业保有生产能力储备的固定成本;ε 为保有生产能力储备成本浮动系数。C5为军队与合同企业实物储备不能满足需求时，采用其他方式获取单位物资的成本。

ω 为军队储备单位物资的保障能力系数;φω为合同企业实物储备单位物资的保障能力系数，且0 ＜φ ＜1;φω 为合同企业生产能力储备单位物资的保障能力系数，且0 ＜φ ＜φ ＜1;γω 为单位物资最低保障能力临界系数。

D为物资需求，其分布函数为F(F为随机分布函数)，概率密度函数为f，D∈(0，Dh)。满足条件:F是连续可微且严格增加，F(0)=0，F(Dh)=1 ，设是需求的期望［4］。为不失一般性，假设C1＜P＜C5。

2.3 模型构建

当军队储备量为λ1D1，合同企业实物储备量为λ2D1时，合同企业生产能力储备量为(1-λ1-λ2)D1时，合同企业的利润期望为

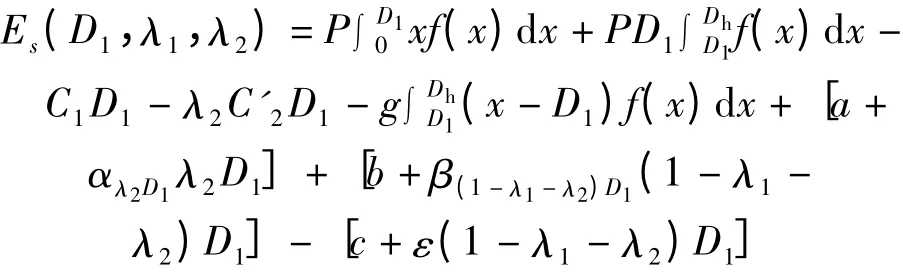
军队利润期望为

整个供应链的利润期望为

该供应链对物资需求的保障能力为W=ωλ1D1+φωλ2D1+ φω(1-λ1-λ2)D1，理想的物资供应链应该使供应链的利润期望达到最大，同时对需求的保障能力也达到最大，即

3 模型的求解

由上文可知，该模型的求解是一个多目标规划问题。为此，可采用约束法将其转化为单目标规划问题［5］。以物资供应链的利润期望为主要目标，对保障能力设定一个期望值，满足保障能力不低于期望值的条件下，使得物资供应链利润期望达到最大，即

引入拉格朗日乘子η 和附加变量θ2，用拉格朗日乘数法构造拉格朗日函数［5］，由式(1)—(3)可得

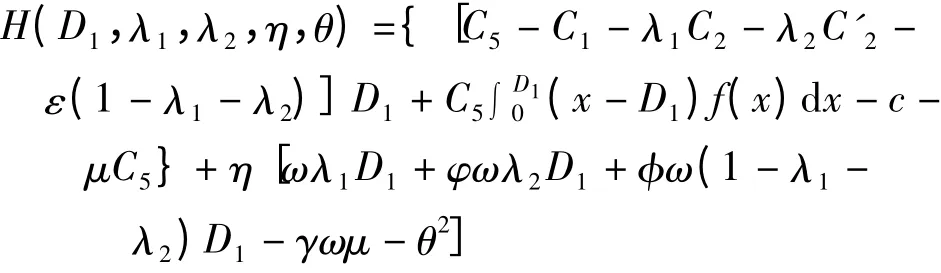
根据拉格朗日函数，极值点存在的必要条件:

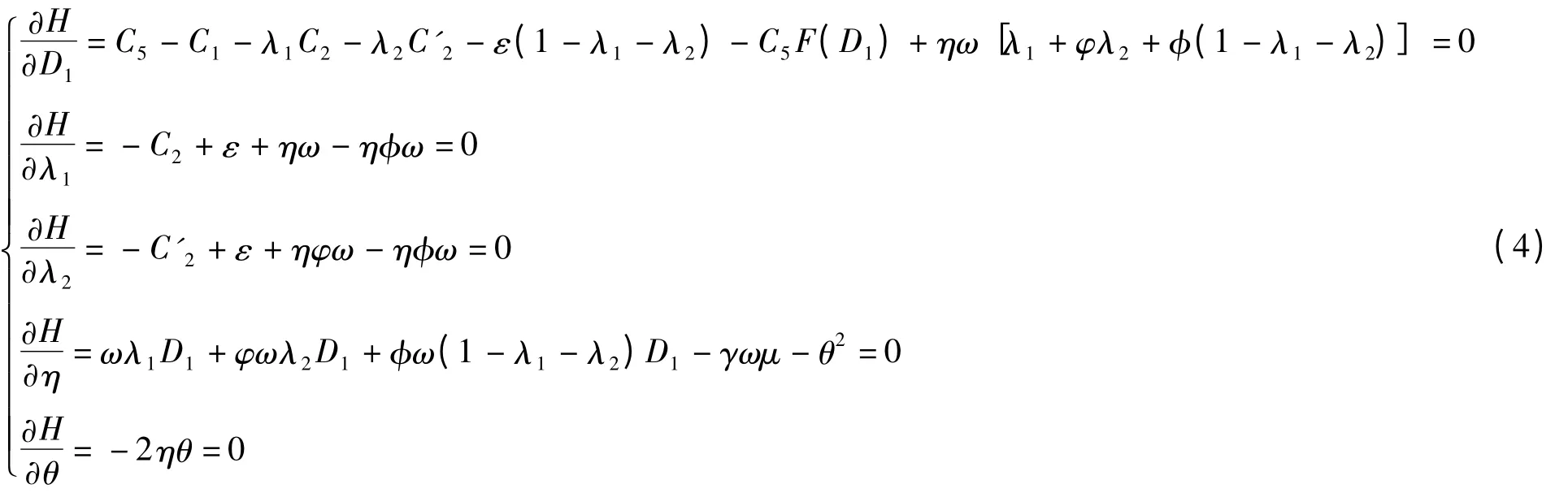
只要给定φ，φ 的取值和分布函数F表达式，便可解出D1、λ1、λ2和η 的取值。又由方程组(4)中第4 式可知，当满足下列的条件时，该供应链的利润期望值达到最大。

4 经济补贴条件分析

4.1 从企业的角度分析

(1)对于合同企业，其利润期望函数应该大于零，即Es=(D1，λ1，λ2)＞0，可得

(2)对合同企业储备总量(1-λ1)D1而言，采用合同企业实物、生产能力储备物资储备总成本应低于全部由合同企业进行实物储备的总成本，即

由此可得

4.2 从军队的角度分析

(1)对于军方而言，对储备总量D1，采用军队与合同企业实物、生产能力储备物资储备总成本应低于全部由军队进行实物储备的总成本，即

由此可得

(2)军队对于合同企业实物储备和合同企业生产能力储备的补贴要小于只采用合同企业实物储备的补贴，即

由此可得

5 实例计算

假设某型号救灾帐篷采取军队与合同企业实物、生产能力储备的形式进行军地联储。该型号每顶帐篷市场采购价格P为2 500 元，单位生产成本C1为1 600 元，军队单位库存成本C2为200元/a，合同企业单位库存成本C'2为120 元/a，合同企业保有生产能力储备的固定成本c为10 000元，军队与合同企业实物储备不能满足需求时，采用其他方式获取单位物资的成本C5为3 000 元。根据合同协议，合同企业物资储备不足时单位惩罚成本g为1 000 元，军队每年向合同企业支付实物储备固定补贴a为1.5 万元，生产能力储备固定补贴b为8 000 元，军队储备单位物资的保障能力ω 为1，合同企业实物储备单位物资的保障能力系数φω 为0.5，合同企业生产能力储备单位物资的保障能力系数φω 为0.2，最低保障能力系数γω 为0.7。

为了使计算简便，假设该型号帐篷的需求服从均匀分布X～U(40 000，120 000)，则由式(4)可得，该型号帐篷总储备量D1为76 266 顶，军队实物储备比例λ1为0.587 3，储备数量约为44 791 顶，合同企业实物储备比例λ2为0.214 9，储备数量约为16 390 顶，合同企业生产能力储备比例为0.197 8，储备数量约为15 085 顶，即合同企业保有15 085 顶左右该型号帐篷的生产能力。此时，整个供应链利润达到最大化，为-3.501 5亿元，对需求的保障能力为56 002。

6 结 语

本文以军地双方围绕物资储备所发生的各种费用为主要依据，以供应链整体利润最大化为目标，以保障能力为约束，构建了军地物资联储经济分析模型，通过该模型可以求解需求随机的情况下的物资总储备量以及军地双方的分摊比例，并可以通过补贴系数的调整实现供应链的协调，达到军地共赢的目的。但在实际操作中，还需考虑军地联储过程中的各种风险和由此产生的军事、经济成本代价，因而本模型也有一定的局限性，这也将是下一步需要研究的问题。

［1］ 金秀满，曾勇，朱晓华. 战备物资企业代储的经济性分析［J］.军事经济研究，2010(3):73.

［2］ 赵彦赟.军民融合式战备物资储备发展策略研究［D］. 北京:后勤学院，2011:26-28.

［3］ 徐东.军队通用物资储备社会化研究［R］. 北京:后勤指挥学院，2009.

［4］ 盛骤，谢式千，潘承毅. 概率论与数理统计［M］. 北京:高等教育出版社，2001:46-48.

［5］ 侯风波，张益池，张国勇，等.高等数学［M］.北京:高等教育出版社，2005.