海上运输补给吊装载荷防摆控制系统研究

杨晓蓉，魏士淇，周永波

(1.军事交通学院 基础部，天津300161;2.军事交通学院 研究生管理大队，天津300161)

将上式展开成分量形式

货物吊装是海上军事行动、工程施工、船舶运输和资源开发中的重要作业形式。风浪是海上最常见的自然现象之一，吊装作业对风浪环境非常敏感，通常，在海浪有义波高超过1 m 时，海上吊装作业即不得不终止［1］。据统计，在世界大部分海区，海况能够进行吊装的时间一般不超过正常工作时间50%，而在我国东海只有34%，在等待可工作海况的过程中浪费了大量的时间和金钱［2］。因此，研究一套控制系统，将货物的摆动减小到可起吊的程度，具有巨大的军事和经济价值。

1 吊物运动分析

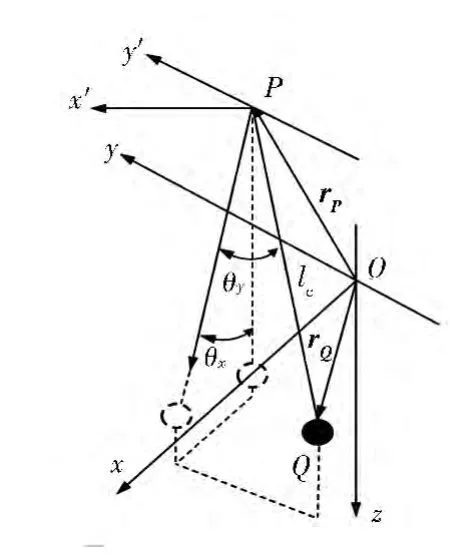
图1 吊物在球惯性系下坐标

本文忽略吊物运动对船体的影响，假定吊杆上的吊物点P处由于船体运动而产生的运动为已知。吊物在球惯性系下坐标如图1 所示。图中rP和rQ分别为吊点和吊物的空间位矢，吊绳长为lc。若已知P点在船舶随体坐标系下的坐标则其在惯性系下的位移、速度和加速度分量分别为［3］

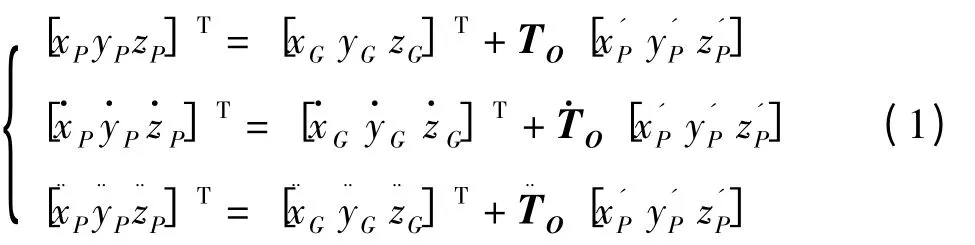
式中TO为坐标变换矩阵。

吊物空间位移可以表示为

通过分析，得出关于面内角和面外角的二阶微分方程组，方程中还考虑了系统阻尼，阻尼以一定比例的临界阻尼施加于吊物，吊物的运动方程表述为

其中n为阻尼系数，一般选取阻尼比ξ 为0.5%～1%以确定阻尼系数n，对于吊物系统，阻尼系数n的表达式为

2 吊物控制系统设计

同时激励吊杆起落角和旋转角，可以使吊杆顶端在吊杆摆动范围内自由移向任何预定的水平位置(如图2 所示)。将延迟定位反馈控制器应用到这些运动上，可以减小吊物的面内和面外摆动。吊杆起重机上本来就存在起落和回转方向的自由度，因此不需要对其结构做重大修改，只需增加部分传感器来测量吊物和吊杆运动［4］。

图2 起重船坐标

为应用延迟控制算法，采用一套位移跟踪控制器来驱动吊杆起落角和旋转角。操作人员输入命令，由延迟定位反馈控制器发出到达位移跟踪控制器。假定起重机的激励器有足够动力，在设计过程中忽略吊杆运动速度的限制。

图2 中，点O是船体运动参考点，过船体重心。坐标系xyz为惯性系。分析中只考虑船体横摇纵摇和垂荡运动，定义坐标系x'y'z'为固定于船体重心并且随船纵摇的随体系，坐标系x″y″z″为坐标系x'y'z'绕y'轴横摇的随体系。

根据图2 所示，吊点P在惯性系下的坐标表达为

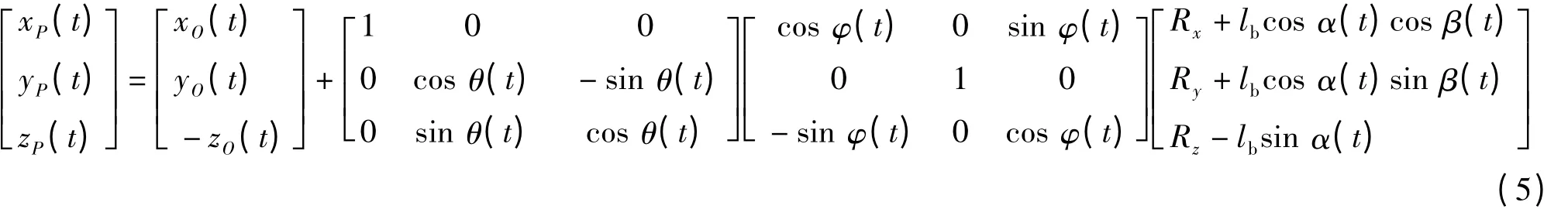
将上式展开成分量形式

式中:lb为吊杆长度;Rx、Ry和Rz为坐标系x″y″z″下起重机基座相对点O的位移。

控制过程中，首先控制器将操作人员给定的起落角αi(t)和旋转角βi(t)转化为吊杆顶端惯性参考点坐标(xi(t)，yi(t)):

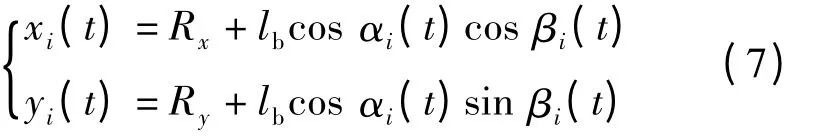
在(xi(t)，yi(t))上施加一定比例的吊物延时运动，构成惯性参考系内吊杆顶端位置:

式中:xref(t)和yref(t)为吊杆顶点位置;kx和ky为θx和θy控制器增益;τx和τy为θx和θy时间延迟。

控制器将(xref(t)，yref(t))替代方程组(3)中悬吊点P的坐标(xP(t)，yP(t))来求解起落角α(t)和旋转角β(t)，控制器的最后一部分包括2 个跟踪PD 控制器，它们是用来快速驱动吊杆的起落和旋转方向的激励器，以跟踪参考角α(t)和角β(t)。

3 数值模拟

采用Fortran 语言编写数值模拟程序，基本流程如图3 所示。

图3 数值模拟流程

3.1 算例模型

算例计算采用某补给船，其参数见表1。计算中选择起重机位置2，吊物重心设置在吊杆顶端下方27.1 m 处，吊摆固有频率为0.096 Hz，阻尼系数为0.002。计算中船体运动取正弦激励，横摇和纵摇频率等于吊摆固有频率，垂荡运动频率为吊摆固有频率2 倍。控制计算中吊物面内和面外时间延迟均设置为2.5 s，约为1/4 吊摆固有周期，增益取0.1。船体横摇幅值为2°，纵摇幅值为1°，垂荡幅值为0.305。

表1 T-ACS 补给船主要尺度和起重机参数 m

3.2 计算结果

进行2 组数值模拟。第1 组数值模拟中，起重机定位在能够使吊杆延伸到垂直于吊杆轴的船体弦侧正上方。吊杆的起落角设定为45°，横摇方向和纵摇方向上给以正弦激励，激励频率等于吊物的固有频率。垂荡方向上施以正弦激励，激励频率等于吊物固有频率的2 倍。吊物在受控与不受控条件下的面内和面外的摆动角如图4、5 所示。在未受控模拟下，吊绳的摆动角随时间快速增大，面内角和面外角最大值均超过65°;在受控情况下，吊物的运动面内角不超过2. 5°，面外角约为1°。

控制器驱动吊杆起落角和旋转角以及速度如图6、7 所示。最大起落速度不超过2 (°)/s，最大旋转速度不超过1 (°)/s，在大部分起重机起落和旋转能力范围之内。

第2 组数值模拟中，起重机定位在能够使吊杆延伸到垂直于吊杆轴的船体弦侧正上方。吊杆的起落角设定为45°，操作员给吊杆一个90°的正弦运动，周期为40 s，之后返回原位。横摇方向和纵摇方向上给以正弦激励，激励频率等于吊物的固有频率。垂荡方向上施以正弦激励，激励频率等于吊物固有频率的2 倍。吊物在受控与不受控条件下的面内和面外的摆动角如图8、9 所示。在未受控模拟下，面内角和面外角最大值分别约为65°和70°;在受控情况下，吊物的运动面内角和面外角极值均为12°左右。

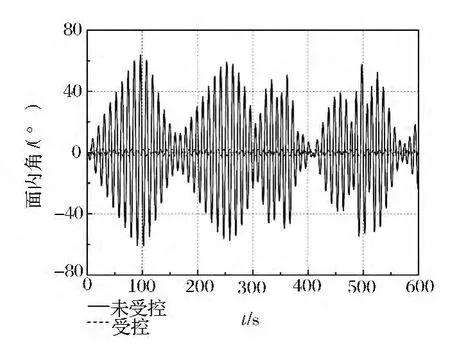
图4 算例1 吊物面内响应

图5 算例1 吊物面外响应

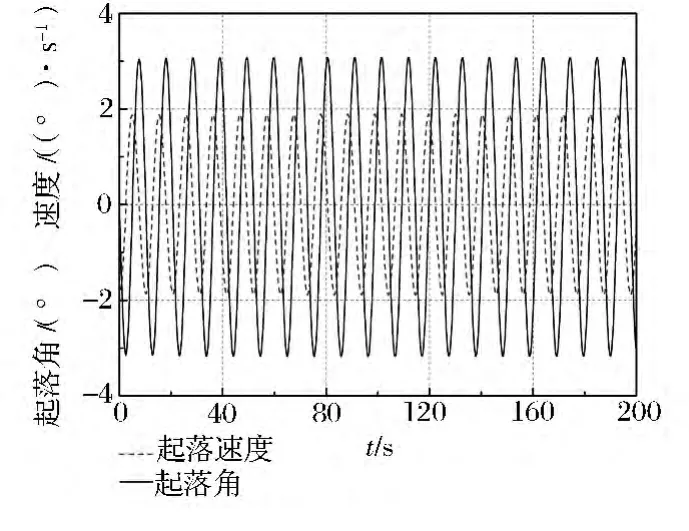
图6 算例1 吊杆起落角与速度时间曲线

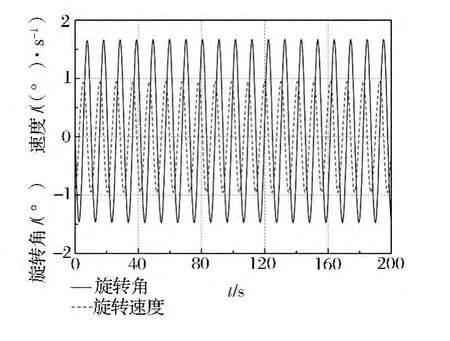
图7 算例1 吊杆旋转角与速度时间曲线

图8 算例2 吊物面内响应

图9 算例2 吊物面外响应

4 结 论

(1)本文建立了吊物运动的球摆型控制方程，吊点水平方向的激励可视为外部激励，垂直方向激励为参数激励，由此确定了吊物最大响应对应的激励参数。

(2)为了研究对吊物摆动的控制，讨论摆动方程组的最大响应的情况，沿x方向和y方向给以接近球摆固有频率的正弦激励，沿z方向给以2 倍于球摆固有频率的正弦激励，来研究控制器的设计。

(3)利用吊物系统的运动方程，按延时定位反馈要求的条件，设计了一种控制系统。设计的关键是参数的选取，包括阻尼系数和控制器增益系数的选取，它们在很大程度上影响了整个控制的效果和适用范围。

(4)通过对比受控情况和不受控情况下的吊物面内角和面外角响应的数值模拟结果可以看出，延迟定位反馈系统可以非常有效地控制海上吊装载荷的摆动。

［1］ 邵曼华，寇雄，赵鹏程.几种船用起重机波浪补偿装置［J］.机械工程师，2004(2):14-16.

［2］ 余建星，顾鹏. 海上干货补给技术［J］. 海洋技术，2005，24(3):105-110.

［3］ 徐小军，陈循，尚建忠. 一种新型主动式波浪补偿系统的原理及数学建模［J］.国防科技大学学报，2007，29(3):118-122.

［4］ Witz J. Parametric excitation of crane loads in moderate sea states［J］. Oeean Engineering，2005(22):411-420.