基于骨架驱动的网格模型变形方法

陆友太，周来水，李运平，王志国

(1.南京航空航天大学江苏省精密与微细制造技术重点实验室，江苏 南京210016;2.中国电子科技集团公司第二十八研究所，江苏南京210007)

三维模型的变形在几何建模和计算机动画中占有重要地位，并得到了广泛应用.总体来说，变形方法主要有几何变形和基于物理的变形这两种，其中使用比较多的是几何变形方法.目前应用比较广泛的几何变形方法是由T.W.Sederberg提出的自由变形(free-form deformation，FFD)方法［1］，该方法被用于几何造型、计算机动画等领域.FFD方法是一种强有力的造型技术，具体操作很直观，但需要进行嵌入坐标换算，而且该方法不易进行变形控制，变形难以精确地达到预期结果.骨架驱动的网格变形方法作为一种重要的自由变形手段，最早由N.Magnenat-Thalmann等［2］提出，其主要思想是将三维网格的变形与人体的运动相类比，将网格表面的点(皮肤)关联到骨架结构，网格变形由骨架的运动来带动.该方法操作简单直观，适合运动变形的应用，且一次建立的骨架模型能被反复使用，因此被广泛应用于人体动画、游戏等领域［3］.骨架驱动变形技术的本质是通过编辑几何模型的骨架来带动几何模型产生形变.该变形方法大致可分为3类:基于仿生学的方法、基于物理的方法和基于几何的方法.总体而言，骨架驱动的网格变形方法已经取得了许多极有理论和应用价值的成果［4-11］，各种方法都有其各自的特点，但寻求更为直观、高效的骨架驱动的网格变形方法，仍是值得研究的重要方向.

文中拟将仿射变换思想和广义元球变形方法［12］运用于骨架驱动变形技术，提出一种基于骨架驱动的网格模型变形新方法.给出带势函数的变形模型，通过兴趣区域网格顶点与骨架模型之间的映射关系，实现网格模型的旋转、平移、缩放变形.这3种变形可以各自独立进行，也可以相互复合以得到用户所需要的变形效果.并且针对对平移变形中出现的失真问题，运用旋转修正方式进行修正.

1 算法概述

首先在网格模型上交互选取变形区域，称为兴趣区域，并创建兴趣区域的骨架模型;进而建立兴趣区域的网格模型顶点与骨架自然坐标之间的映射;然后，根据需要选择相应的带势函数的变形模型(旋转、平移或缩放)，并给出变形目标(旋转轴和旋转角度、平移的目标点或偏移量、缩放比例等);最后根据兴趣区域网格顶点与骨架的对应关系，计算出网格顶点变形后的新位置，得到变形结果.图1以平移变形为例显示了本文方法的基本变形过程.

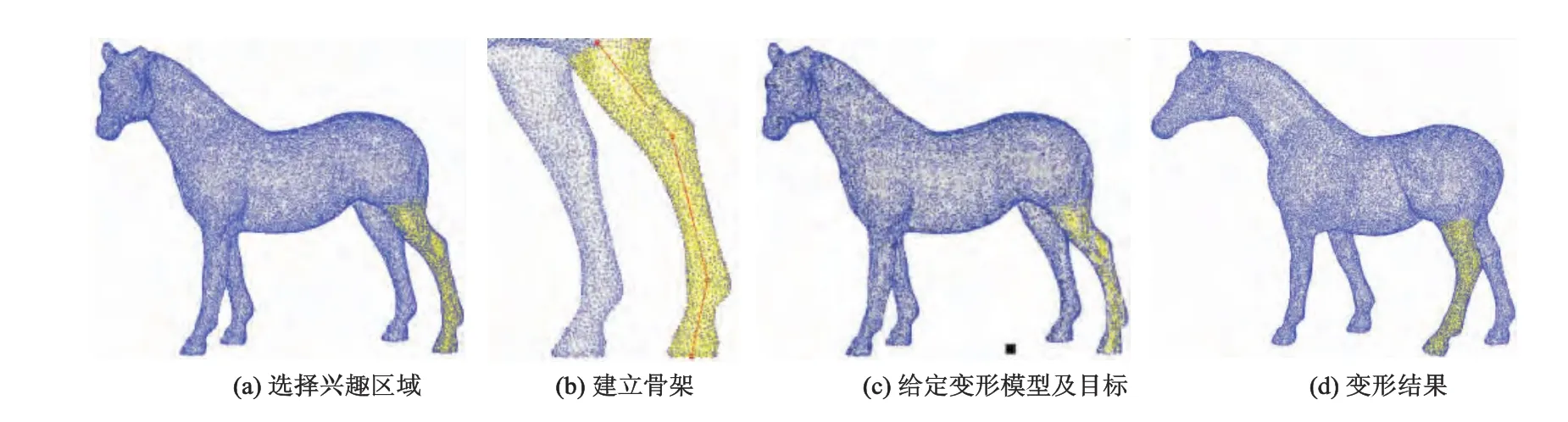
图1 本文方法的变形过程

2 基于骨架驱动的网格变形

2.1 选取兴趣区域

文中给出了2种确定兴趣区域的方法.一种方法是在网格上选取2个顶点，对第1个顶点的邻接顶点进行广度优先搜索，直到遇到第2个顶点，则包含这些遍历过的顶点的网格区域就是兴趣区域.此外，针对比较简单的网格模型，文中提供了一种简单、直观的选取方式，即允许用户通过鼠标直接在屏幕上画一个矩形(或任意封闭曲线、多边形均可)进行选取，矩形框住的区域就是兴趣区域.

2.2 创建兴趣区域骨架模型

针对选定的兴趣区域，文中采用S.Capell等［4］提出的光线求交法来获取其对应的骨架.通过鼠标点击屏幕处作为垂直于屏幕的光线的入射点，以光线与网格模型交点S1，S2所构成线段的中点S作为骨架的关节点，若光线与网格模型只有一个交点，那么就以该点作为关节点，这样鼠标每点击一次都会产生一个关节点.

根据兴趣区域网格模型的形状(如图1a所示，马的左后腿为选定的兴趣区域)，先通过调整网格模型的姿态，使兴趣区域网格模型的中轴方向大致与屏幕平面平行(如图1b所示);然后根据兴趣区域网格模型的形状，沿其大致的中轴方向依次创建骨架关节点(如图1b所示，自下而上依次创建了4个骨架关节点)，依次连接这些关节点，即可获得兴趣区域网格模型所对应的骨架模型.将开始和最后产生的关节点看作骨架的两个端点，各关节点之间的连接线称为骨架线.图2所示为采用光线求交法得到Horse的骨架模型.

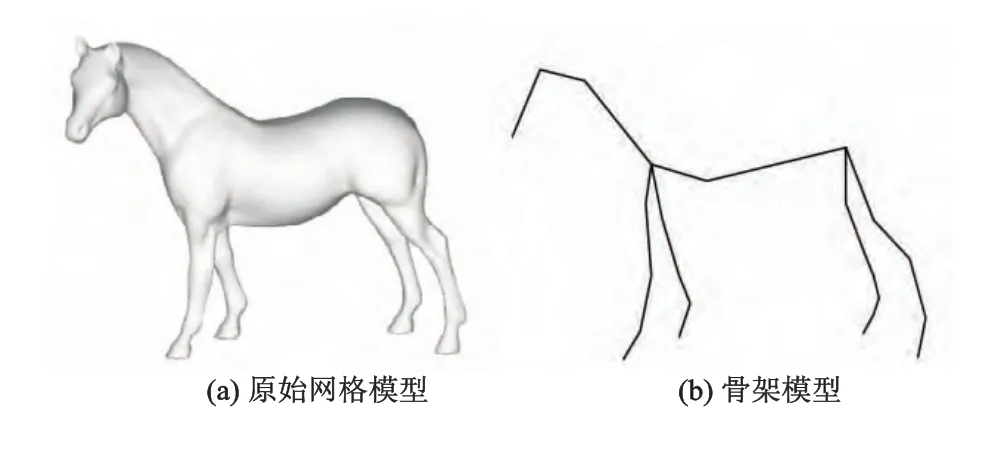
图2 光线求交法生成骨架模型

2.3 建立网格模型顶点与骨架的映射

兴趣区域骨架模型建立后，需建立兴趣区域网格模型顶点与骨架自然坐标之间的映射，且该映射关系在变形过程中保持不变.具体计算过程如下:

1)将兴趣区域的网格顶点垂直映射到骨架线上，如图3所示，骨架线上的点Si即为网格顶点pi相对应的映射点.骨架线两端的两条线段可以看作方向分别指向骨架端点的两条射线.映射后，沿着骨架线的方向分别与两个端点距离最大的两个映射点记作起始映射点和终映射点，沿骨架线计算所有映射点与起始映射点的距离.

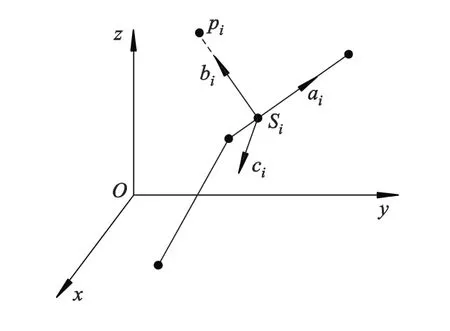
图3 网格顶点与骨架模型的映射

2)建立兴趣区域中网格顶点所关联的映射点的局部坐标系.如图3所示，映射点Si处的局部坐标系记为(ai，bi，ci)，起始映射点的坐标轴 ai为由该点指向下一个映射点的单位向量，终映射点的坐标轴ai为上一个映射点指向该点的单位向量，中间映射点的坐标轴ai为前一个映射点指向该点的单位向量和该点指向下一个映射点的单位向量相加并归一化所得到的单位向量;坐标轴bi为该点指向其对应的网格点的单位向量;ci是与ai和bi垂直的单位向量.对(ai，bi，ci)进行 Schmit正交化后形成一个右手直角坐标系.对兴趣区域上的每个网格顶点都分别用其映射点的局部坐标系进行标示.

2.4 定义变形模型

文中将变形模型定义为带势函数的仿射变换，即以起始映射点为约束源，沿骨架线从起始映射点到终映射点的距离R为约束半径，以仿射变换矩阵为变形矩阵(旋转、平移、缩放)，然后根据骨架上各映射点到约束源的距离来确定各点处的变形权值进行变形.

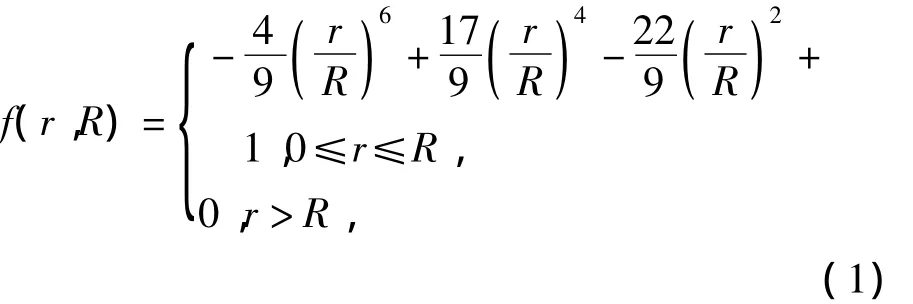
式中:r为骨架上的映射点与约束源¯S沿骨架线的距离;R为约束的有效半径;f(r，R)为相对于¯S的势函数.对于任意映射点Si，利用式(1)均可以计算出其场值fi(r，R)，作为该点处变形的权值.

2.4.1 旋转变形

要表示物体的旋转，可以采用欧拉变换，但采用欧拉变换可能会带来万向节死锁的问题，因此文中采用了四元数法.假设要让空间点p=(x，y，z)T绕单位轴 u旋转 θ角度，则有单位四元数 q=，旋转矩阵为

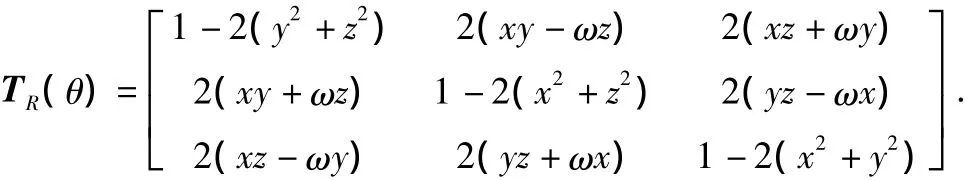
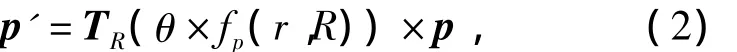
式中:p'为p经旋转变形后的新顶点;fp(r，R)为约束源¯S在点p对应的映射点Sp处的变形权值.

若要让兴趣区域的网格模型对任意旋转轴做旋转变形，文中的方法是先在终映射点处建立一个局部坐标系，然后将兴趣区域网格模型变换到该局部坐标系中进行旋转变换，最后再将局部坐标系变换回全局坐标系，得到旋转变形结果.

2.4.2 平移变形

假设p是兴趣区域网格模型上的点，其对应的映射点为 Sp，d=(dx，dy，dz)T是变形目标 ¯S'相对于约束源¯S的最大偏移量，fp(r，R)是约束源¯S在点Sp处的变形权值.则点p变形后的新顶点p'的坐标为

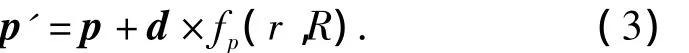
事实上，此平移变形只是相当于对点Sp处的局部坐标系进行了平移，这就使得变形前垂直于骨架线的横截面经平移变换后不再保持垂直关系，如图4a，4c所示，因此需要对变形结果进行修正.文中采用旋转修正的方法对变形结果进行修正，具体思路如下:对应于变形前Sp处的局部坐标系的坐标轴ap，变形后S'p处相应的坐标轴a'p仍用2.3节中的方式进行定义，记ap与a'p间的夹角为βp，如图4a所示.若点p在局部坐标系下的坐标为Pl=(xl，yl，zl)T，则在平移变形后需对其在原局部坐标系下绕单位轴旋转 β 角度.图 4c，4d 给p出了修正前后的变形效果对比，可以看出，经修正后的变形更符合真实的变形效果.

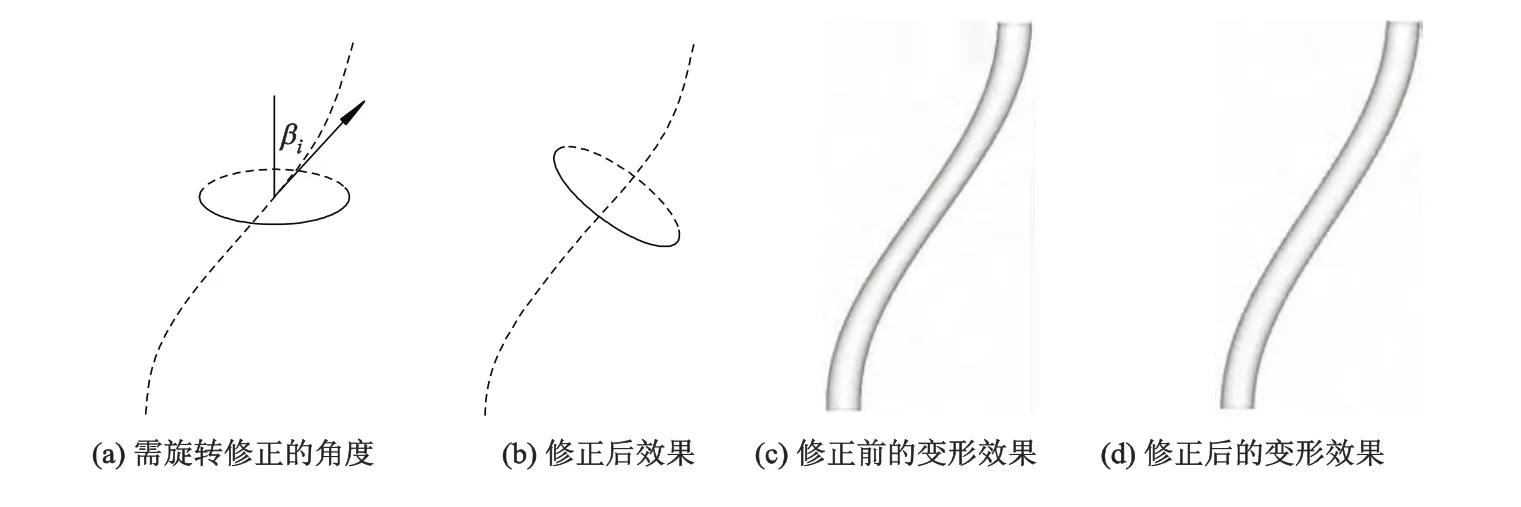
图4 平移变形修正前后的效果对比

2.4.3 缩放变形

缩放变形是比较简单的变形方式，可以在全局坐标系下进行，也可以先在局部坐标系下进行缩放变形，然后再变换回全局坐标系.前者更适合大变形的情形，而文中则采用后面一种方式进行缩放变形.

假设在约束源处的最大缩放比例为s=(sx，sy，sz)T，则有缩放变换矩阵为

对任意点p=(x，y，z)T的缩放变形公式为

式中:p'为p经缩放变形后的新顶点;fp(r，R)为约束源¯S在点p对应的映射点Sp处的变形权值.

若要对兴趣区域的网格模型做缩放变形，则类似旋转变形先在终映射点处建立一个局部坐标系，将兴趣区域网格模型变换到该局部坐标系中进行缩放变换，最后再将局部坐标系变换回全局坐标系，得到缩放变形结果.

前面分别讨论了针对旋转、平移和缩放变形的计算.这3种变形可以各自独立进行，也可以相互复合以得到用户所需要的变形效果.

3 试验结果

在VC++6.0开发环境下，在CPU为Pentium Dual_Core 2.2 GHz，RAM为2 GB的PC机上实现了文中算法.通过交互选取兴趣区域，实现网格模型整体和局部的变形.试验表明，当模型的三角片数目在10万个以下时，系统基本上能达到实时的效果.

图5所示是对Homer模型腿部进行的平移变形结果，其中图5a为初始网格模型，图5b显示了向后抬起右腿的效果，图5c所示为迈步行走的效果.

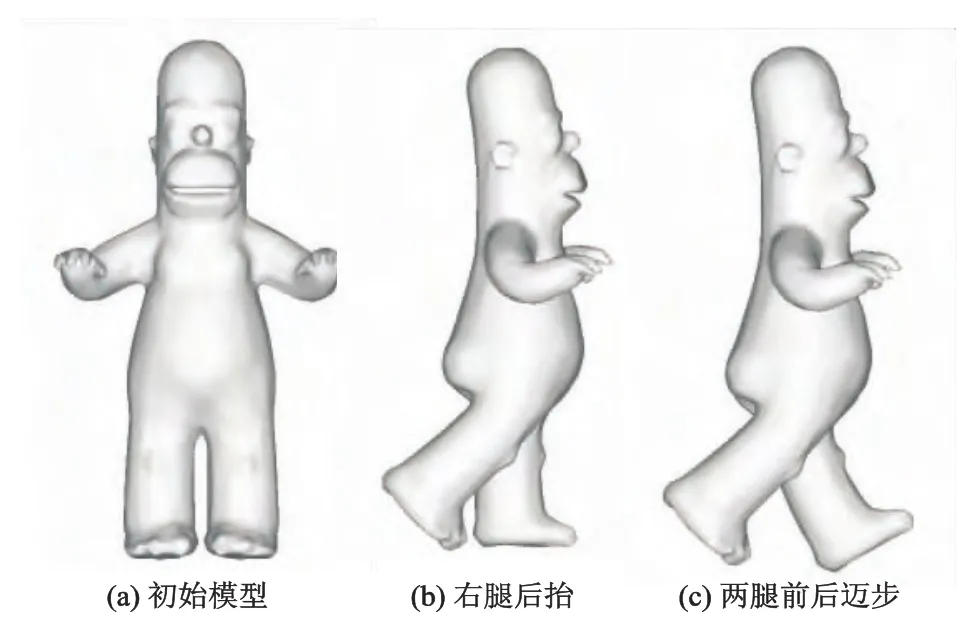
图5 Homer模型变形结果

图6显示了对兔子模型左耳的变形结果，选取兔子左耳作为兴趣区域，并建立相应骨架模型，分别进行了平移(图6b)和旋转变形(图6c，6d)，得到了左耳拉伸、弯曲和扭曲的结果，其中图6d的旋转轴定义为沿骨架线方向不断变化的单位向量.

图7显示了局部缩放的变形效果，对螺丝刀的刀头部分进行了缩小、手柄部分进行了放大.

图8所示是将一个手模型的大拇指和食指进行弯曲变形的结果，在变形操作过程中，为了使变形效果更加逼真，实际上对手指的各指节采用了不同的旋转角度，图8b是对初始模型做多次旋转变形而得到的结果.

图6 兔子模型局部变形结果

图7 对螺丝刀模型的缩放变形结果

图8 对手模型的变形结果

4 结论

文中提出了一种基于骨架驱动的网格模型变形新方法，可方便地实现网格模型的旋转、平移、缩放变形.试验结果表明，利用本文方法进行变形能够很好地避免经典变形方法在非变形区产生的扭曲现象，并且能够较好地保持变形区域网格模型的局部特征.

在文中方法中，骨架是由各关节点依次用直线段连接产生的，也可以根据不同形状的兴趣区域用不同的曲线拟合产生，从而使变形结果更加精确;此外，本变形方法是以网格模型的骨架来带动网格模型变形，在后续的研究工作中，将尝试把变形模型直接作用到网格模型上，而无需建立网格模型的骨架，进一步研究网格模型的直接约束变形.

References)

［1］Sederberg T W，Parry S R.Free-form deformation of solid geometric models［J］.Computer Graphics，1986，20(4):151-160.

［2］Magnenat-Thalmann N，Laperrière R，Thalmann D.Joint-dependent local deformations for hand animation and object grasping［C］∥Proceedings of Graphics Interface'88.Canada:Edmonton，1988:26-33.

［3］胡事民，杨永亮，来煜坤.数字几何处理研究进展［J］.计算机学报，2009，32(8):1451-1469.Hu Shimin，Yang Yongliang，Lai Yukun.Research progress of digital geometry processing［J］.Chinese Journal of Computers，2009，32(8):1451-1469.(in Chinese)

［4］Capell S，Green S，Curless B，et al.Interactive skeleton-driven dynamic deformations［J］.ACM Transactions on Graphics，2002，21(3):586-593.

［5］Yan Hanbing，Hu Shimin，Martin Ralph R，et al.Shape deformation using a skeleton to drive simplex transformations［J］.IEEE Transactions on Visualization and Computer Graphics，2008，14(3):693-706.

［6］许秋儿，谭光华，张三元，等.保持几何特征的均值骨架子空间网格变形［J］.计算机辅助设计与图形学学报，2009，21(3):289-294.Xu Qiuer，Tan Guanghua，Zhang Sanyuan，et al.Lo-cality preserving mesh deformation based on mean-value skeleton subspace［J］.Journal of Computer-Aided Design＆Computer Graphics，2009，21(3):289-294.(in Chinese)

［7］Wang Zhiguo，Wang Xiaoping，Bao Yidong，et al.Shape modification by beam model in FEM［J］.Chinese Journal of Aeronautics，2010，23(2):246-251.

［8］许秋儿，欧阳毅，张三元，等.基于均值骨架的网格变形复制［J］.浙江大学学报:工学版，2010，44(4):710-714.Xu Qiuer，Ouyang Yi，Zhang Sanyuan，et al.Mesh deformation transfer based on mean-value skeleton［J］.Journal of Zhejiang University:Engineering Science，2010，44(4):710-714.(in Chinese)

［9］董洪伟.网格变形综述［J］.中国图象图形学报，2011，16(12):2095-2104.Dong Hongwei.Survey of mesh deformation ［J］.Journal of Image and Graphics，2011，16(12):2095-2104.(in Chinese)

［10］李运平，周来水，王 琳，等.刚架模型驱动网格曲面保特征变形［J］.南京航空航天大学学报，2012，44(4):526-531.Li Yunping，Zhou Laishui，Wang Lin，et al.Preserving form feature in mesh surface deformation via rigid frame［J］.Journal of Nanjing University of Aeronautics＆Astronautics，2012，44(4):526-531.(in Chinese)

［11］韩 丽，齐晓明.骨架驱动的三维模型变形方法［J］.计算机工程与设计，2012，33(3):1051-1056.Han Li，Qi Xiaoming.Multi-skeleton-node driven local deformation method for 3D mesh model［J］.Computer Engineering and Design，2012，33(3):1051-1056.(in Chinese)

［12］Jin Xiaogang，Li Youfu，Peng Qunsheng.General constrained deformations based on generalized meatballs［J］.Computer＆Graphics，2000，24(2):219-231.