二维后向台阶层流传热特性的数值模拟
仲敏波,谢纬安,袁银男,,喜冠南,
(1.江苏大学能源与动力工程学院,江苏镇江212013;2.南通大学机械工程学院,江苏南通226019)
在能源、动力、机械过程的许多管内换热设备中,通过改变流道截面,使流体发生分离,能达到强化换热的目的[1].后向台阶虽然几何结构简单,但因为分离点固定,而且包含着分离流动的一系列特征,常被作为研究分离流动的基准模型之一.
迄今,针对后向台阶流动已经有了大量的试验[2-5]和数值研究[6-10].B.F.Armaly 等[2]首次对同一模型同时进行了试验和数值研究,通过对比发现层流状态下的二维数值模拟结果和试验结果吻合,而随着雷诺数(Re)增大,由于台阶侧壁的影响,数值模拟结果偏离试验结果.之后,众多的科研工作者对这一复杂的流动结构进行了研究.然而,现有的关于后向台阶的研究大部分只针对流动特性和相关的流场,只有少部分是针对后向台阶的传热特性.H.Chaudhary等[11]通过二维数值模拟研究了层流(Re=1~200)时,Re和Pr的变化对流动和传热特性的影响;孙正中等[12]研究了湍流时台阶下壁面温度变化对通道内部温度分布的影响.笔者通过数值模拟方式研究层流状态下,雷诺数和台阶几何参数(台阶高度、平板间高度)的变化对台阶底面传热特性的影响,并结合流场中流动结构的变化对传热特性的分布规律进行分析.这对指导层流状态下管内换热设备的结构优化,提高换热设备的换热效率具有重要意义.
1 模型的建立和验证
1.1 控制方程
数值模拟研究流体流过二维后向台阶后的流动传热情况.以连续、不可压缩流体(空气)为研究对象,所采用的控制方程包括质量守恒、动量守恒和能量守恒方程:
质量守恒方程为
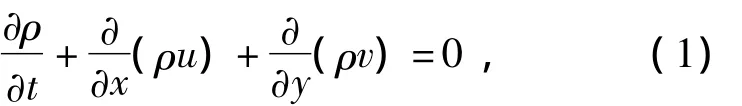
式中:u,v分别为x,y方向速度分量;ρ为流体密度.
动量守恒方程为
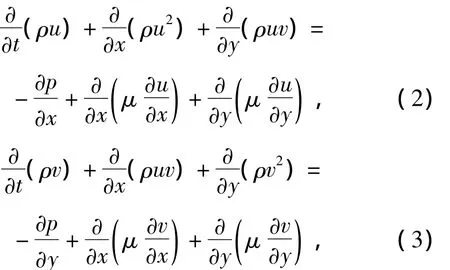
式中:p为压力;μ为黏性系数.
能量守恒方程为

式中:cp为定压比热;h为比焓;λ为热导率.
1.2 计算区域和边界条件
二维后向台阶流动的计算区域如图1所示.
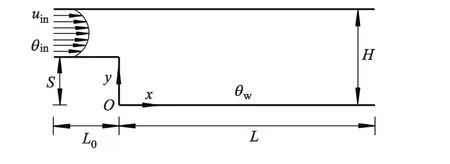
图1 后向台阶计算区域
采用直角坐标系建立数值模型,坐标原点O位于台阶垂直壁面和下游底面的交点处,x方向为沿着流体流动方向,y方向为垂直于流体流动方向.S为台阶高度,H为平板间高度,L0为台阶上游进口长度,L为台阶下游出口长度,ER=H/(H-S)为台阶扩张比.数值计算设定的初始条件:进口边界处的温度均匀分布θin=10℃,进口速度uin充分发展,满足抛物线分布;出口边界处的速度场和温度场符合边界层近似理论.壁面边界:台阶所有壁面速度无滑移,台阶下游底面被等温加热θw=40℃,其余壁面绝热.
1.3 网格划分和模型验证
采用非均匀网格划分计算区域,由于流动参数在台阶分离点处和台阶上、下平板壁面处的变化梯度较大,为了保证计算结果的准确性,需要对上述区域附近的网格加密.对计算区域划分网格时,保证台阶分离点处的网格间距为最小,保证流向和法向的首个、末个网格间距分别为相邻网格间距的0.5倍.
数值模拟采用课题组自行编制的FORTRAN计算程序.求解控制方程时,首先采用基于交错网格的有限容积法离散控制方程,离散过程中动量方程的对流项和扩散项分别采用三阶迎风差分(QUICK算法)和二阶中心差分格式,时间项采用隐式求解法.对离散后的方程求解时,每一个时间步采用ADI算法,压力场的修正采用SIMPLE法则.
为了验证数值计算方法的可靠性,对相同工况下计算得到的流体再附着点位置xr与前人相关的试验和数值模拟结果进行了对比,结果如图2所示,按以上数值模型计算的结果与文献[6]中ER=2.00的数值模拟数据表现一致,与文献[2]中ER=1.94的试验数据之间存在一个差异(随着Re的增大,数值模拟结果低于试验结果).通过验证表明文中所用数值计算方法是正确可靠的.

图2 再附着点位置比较
2 计算结果与讨论
2.1 台阶底面努塞尔数和表面摩擦因数的分布
文献[2]以ER=1.94的台阶作为研究对象,以台阶进口高度(Hin=H-S)的2倍(2Hin)作为特征高度,得到Re2Hin<1 200时,流场处于层流状态.将这一范围换算到以台阶高度(S)作为特征高度,对应的层流Re数范围为ReS<565.所以,文中的研究范围定为Re=100~400.
台阶扩张比ER=2.00,台阶上游进口长度L0=S,下游出口长度L=100S.台阶高度S作为特征量,相应的Re和Nu分别定义为

式中¯uin为流体进口平均速度.
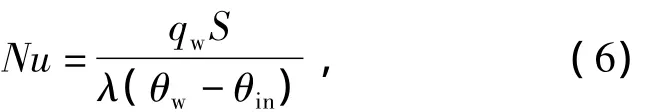
式中qw为热流密度.
流场稳定后台阶下游底面努塞尔数Nu的分布情况如图3所示.从图中可以观察到以下特征:①Re一定时,沿着流体流动方向,Nu先迅速增大,到达峰值后又迅速减小,沿程只有1个峰值,在主回流区,Nu随着距台阶距离的增加而快速增加,到达再附着点时,Nu达到峰值,换热效率达到最大,在再附着点下游,Nu随着距台阶距离的增加先快速减小,然后慢慢减小;②随着Re的增大,Nu的变化范围也越大,峰值越大且峰值位置随着Re的增加向下游移动,Re从100增加到400,峰值位置由x/S=5处变化到x/S=12处;③Re≥300时,Nu变化曲线在下降段有个明显的曲折点,且曲折点的位置稳定在x/S=22处,在曲折点下游Nu受Re的影响不大.
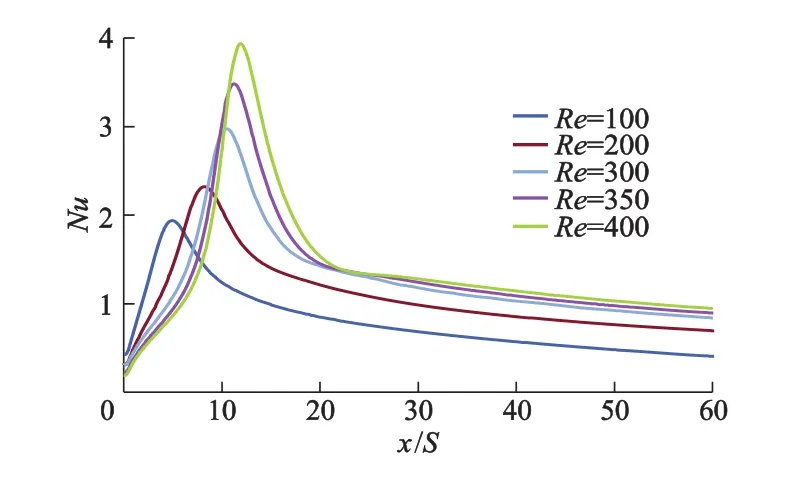
图3 ER=2.00台阶底面努塞尔数的分布
对应工况下,流场稳定后台阶底面摩擦因数Cf的变化规律如图4所示.
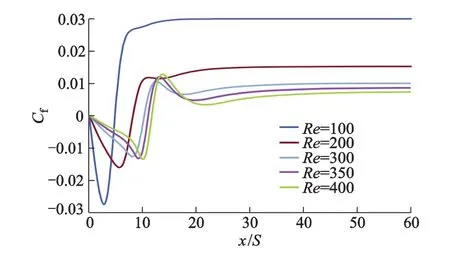
图4 ER=2.00台阶底面表面摩擦因数的分布
从图4可以观察到以下特征:①Re分别为100,200时,Cf沿着流动方向,先由0迅速减小,到达最小值后又迅速增大到0,然后继续向正值方向增大到最大值,之后Cf的变化比较平缓;②Re≥300时,Cf到达最大值后又出现下降.Re越大,Cf下降也越多;③ 随着Re的增大,Cf的变化范围减小,再附着点的位置(Cf=0)向下游移动.
2.2 流场与温度场
Re变化时ER=2.00的后向台阶流动达到稳定后内部流场的变化情况图5所示,Re为100和200时,流场只在靠近台阶处存在一个主回流区域.当Re≥300时,位于主回流区域下游靠近台阶上平板壁面又出现了1个二次回流区域.二次回流区域的出现,挤压了流体的中间流道,使流体的速度增加,而压力减小,对应位置的Cf出现下降,如图4所示.流线和速度矢量图如图5所示,标“▲”处表示再附着点位置,Re越大,主回流区长度越长.
随着Re增大温度分布云图的变化情况如图6所示,图中的曲线表示等温线.流体在台阶角点发生分离,经过一段距离后,流体和壁面重新接触,在再附着点处(图中标“▲”的位置),由于流体冲击壁面,壁面温度边界层破坏,温度变化梯度最大,图3中底面Nu在对应位置达到最大.
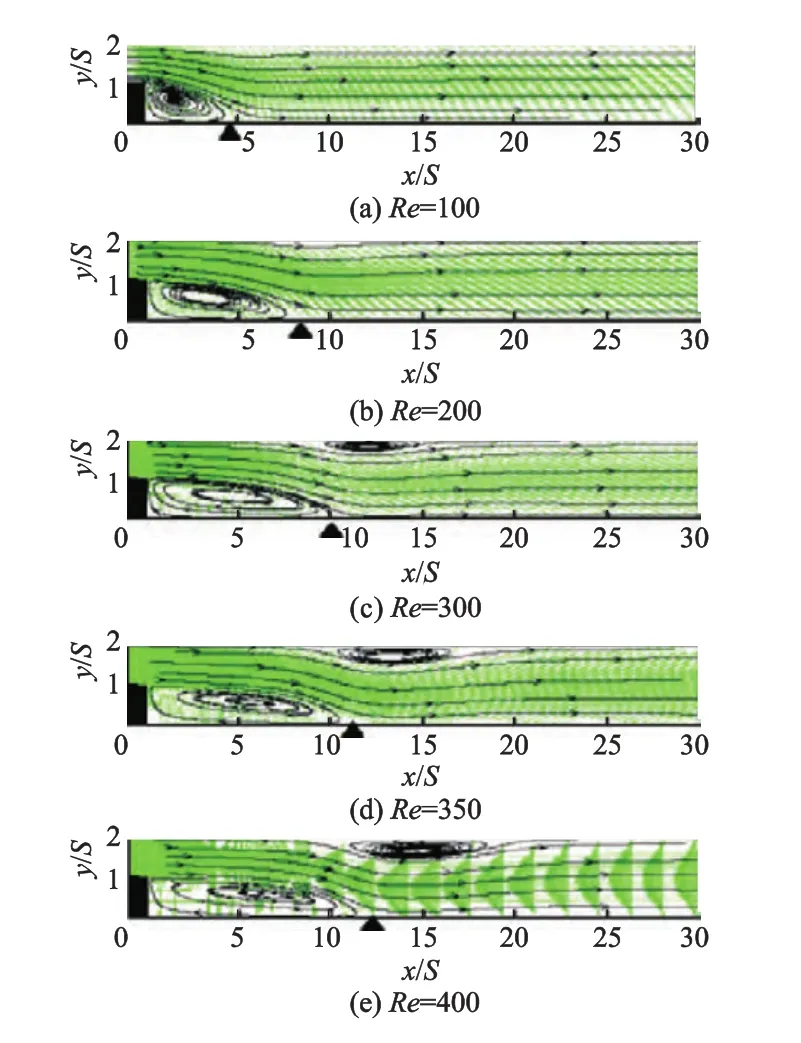
图5 流线和速度矢量图 (ER=2.00)
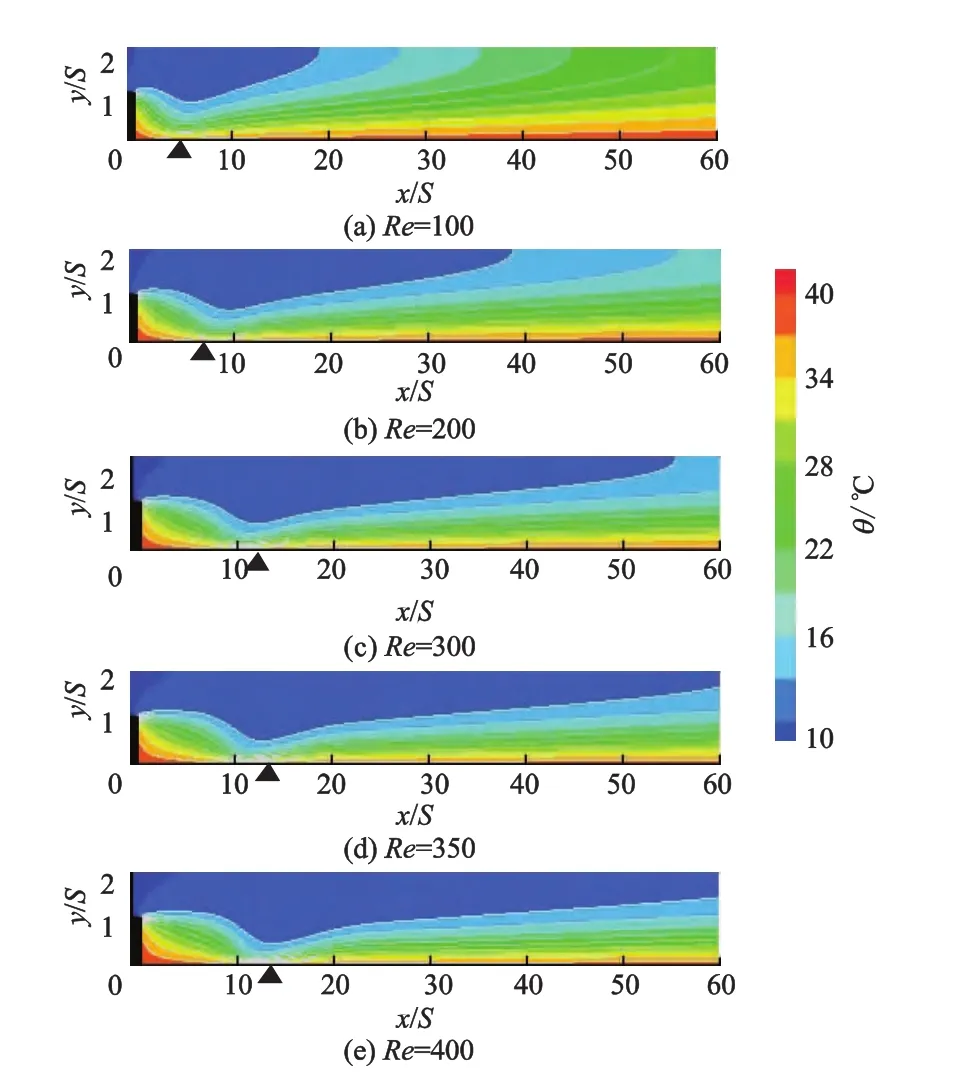
图6 温度分布云图(ER=2.00)
当Re≥300,台阶上壁面出现二次回流区后,底面Nu变化曲线在下降段的曲折点固定.图7,8比较了Re分别为300,350,400时后向台阶流道剖面上的量纲一速度、温度沿法向的分布.选择6个流道剖面,其中,剖面x/S=0,5,10,16位于曲折点上游,剖面x/S=22位于曲折点处,剖面x/S=28位于曲折点下游.从图7,8可以看出:由于进口速度不同,曲折点上游各剖面上的速度和温度沿法向的变化并不一致;在剖面x/S=22处,速度和温度在靠近底面处的变化梯度表现一致;在剖面x/S=28处,速度和温度沿法向的变化大致相同.
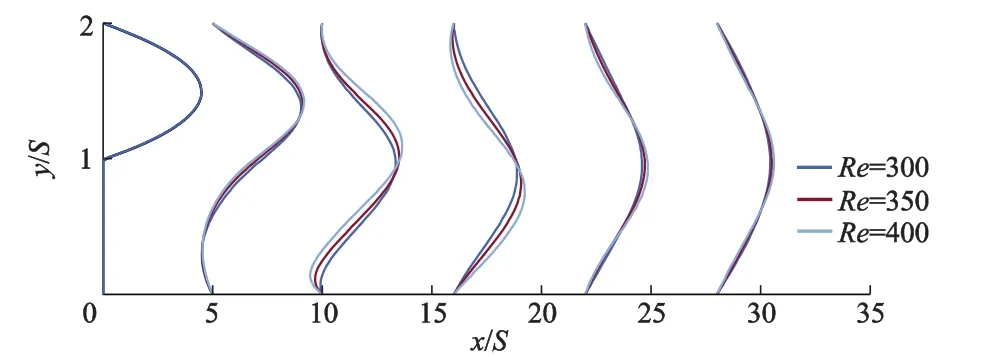
图7 法向速度分布 (ER=2.00)

图8 法向温度分布 (ER=2.00)
2.3 平板间高度变化对台阶底面Nu分布影响
保持台阶高度S不变,改变平板间高度H,图9,10分别表示ER=1.50,3.00 时台阶底面Nu随Re的变化.
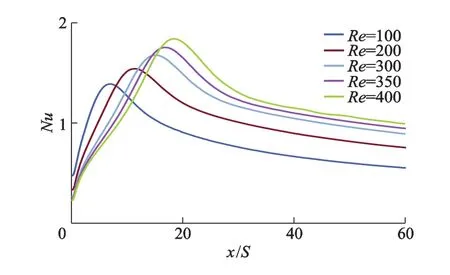
图9 ER=1.50台阶底面努塞尔数的分布
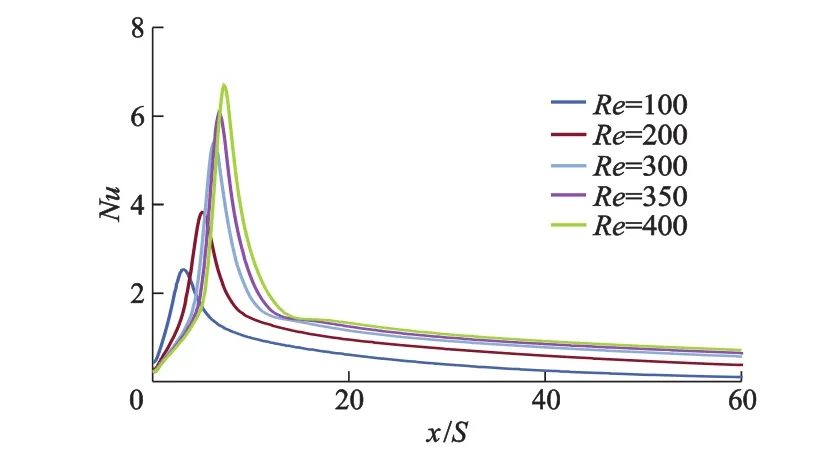
图10 ER=3.00台阶底面努塞尔数的分布
从图9,10可以看到,ER一定时,Nu的变化规律和图3相似,但随着ER的增大,Re的变化对Nu峰值的影响也增大.ER=1.50,2.00,3.00 时,Re从100 增大到400,Nu的峰值分别增加了约 1.3,2.0,2.6倍.图9中ER=1.50时,由于Re≤400时台阶下游上壁面还未出现二次回流区,Nu变化曲线在下降段未出现固定的曲折点;图10中ER=3.00时,由于Re≥300时台阶下游上壁面出现了二次回流区,Nu变化曲线出现了1个固定的曲折点.Re≥300后,ER由 2.00增大到 3.00,该曲折点的位置由x/S=22处向上游移动至x/S=15处,但曲折点处Nu仅由1.38增加到1.41.所以台阶上壁面出现二次回流区域后,增大ER能提高曲折点上游的Nu,但对曲折点下游的Nu影响较小.
台阶进口速度保持0.190 8 m·s-1不变,Re=200,S=15.0 mm,H=22.5,25.0,30.0,45.0,60.0 mm时,台阶底面Nu的分布如图11所示.
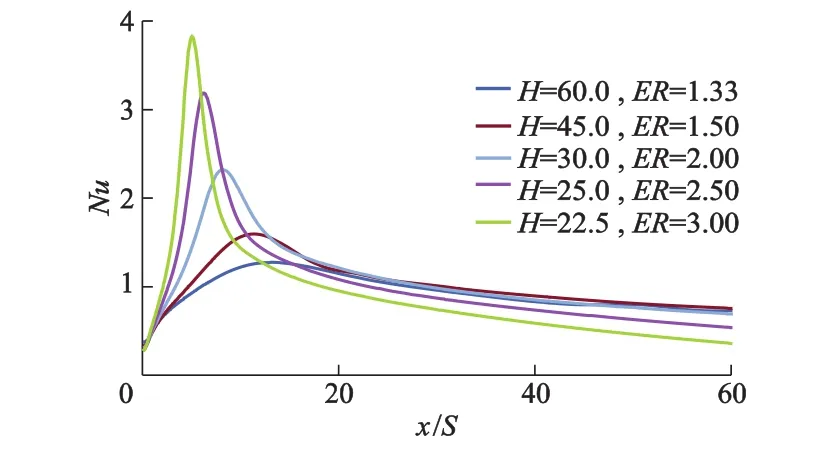
图11 相同S,不同H下底面努塞尔数的分布
从图11可以看出:H由60.0减小到22.5,ER由1.33增加到3.00,Nu的变化范围随H减小而增大,Nu峰值的位置随H减小向上游移动.
2.4 台阶高度变化对台阶底面Nu分布影响
保持平板间高度H不变,改变台阶高度S.以H作为特征量,Re和Nu分别记为ReH和NuH,定义为
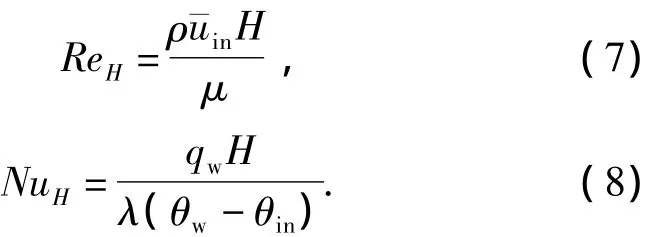
台阶进口速度保持0.190 8 m·s-1不变,ReH=400,H=30.0 mm,S=7.5,10.0,15.0,18.0,20.0 mm时,台阶底面NuH的分布如图12所示,S由7.5增加到20.0,ER由 1.33 增加到 3.00.NuH的变化情况分2部分:S由7.5增加到15.0,ER由1.33增加到2.00,NuH的峰值基本不变,但峰值位置随着S增加向下游移动;S由15.0增加到20.0,ER由2.00增加到3.00,NuH的峰值快速增加,但峰值的位置随着S增加变化不大,位于x/H=4附近.
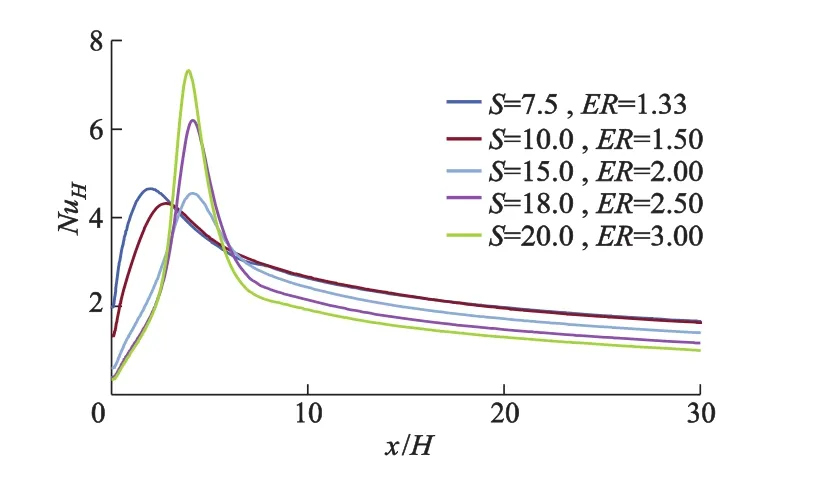
图12 相同H,不同S下底面努塞尔数的分布
3 结论
1)数值模型计算得到的流体再附着点位置与现有的试验和计算结果吻合,说明计算模型可靠,计算结果正确有效.
2)随着Re的增大,台阶上平板壁面出现二次回流区后,Nu变化曲线在下降段有一明显的曲折点.Re继续增大,曲折点的位置稳定,在曲折点下游Nu受Re的影响不大.台阶上壁面出现二次回流区域后,增大ER能提高曲折点上游的Nu,但对曲折点下游的Nu影响较小.
3)保持S不变,减小H,ER由1.33增加到3.00,Nu的变化范围增大,Nu峰值的位置向上游移动.
4)保持H不变,增大S.ER由1.33增加到2.00,NuH峰值基本不变,但峰值的位置随着ER增加向下游移动;ER由2.00增加到3.00,NuH峰值快速增加,但峰值的位置随着ER增加基本不变.
References)
[1]苏 磊,张 红,丁雷江,等.单回路脉动热管传热性能的试验[J].江苏大学学报:自然科学版,2012,33(1):49-54.Su Lei,Zhang Hong,Ding Leijiang,et al.Experiment on heat transfer characteristics of single loop pulsating heat pipe[J].Journal of Jiangsu University:Natural Science Edition,2012,33(1):49-54.(in Chinese)
[2]Armaly B F,Durst F,Pereira J C F,et al.Experimental and theoretical investigation of backward-facing step flow[J].J Fluid Mech,1983,127:473-496.
[3]齐鄂荣,黄明海,李 炜,等.二维后向台阶流流动特性的实验研究[J].实验力学,2006,21(2):225-232.Qi Erong,Huang Minghai,Li Wei,et al.A experimental study on the 2D time-average flow over a backward facing step via PIV [J].Journal of Experimental Mechanics,2006,21(2):225-232.(in Chinese)
[4]Tihon J,Pěnkavová V,Šimík H M,et al.The transitional backward-facing step flow in a water channel with variable expansion geometry[J].Experimental Thermal and Fluid Science,2012,40:112-125.
[5]Chen Z,Yi S H,Tian L F,et al.Flow visualization of supersonic laminar flow over a backward-facing step via NPLS[J].Shock Waves,2013,23:299-306.
[6]Iwai H,Nakabe K,Suzuki K.Flow and heat transfer characteristics of backward-facing step laminar flow in a rectangular duct[J].International Journal of Heat and Mass Transfer,2000,43(3):457-471.
[7]Barri M,El Khoury G K,Andersson H I,et al.DNS of backward-facing step flow with fully turbulent inflow[J].International Journal for Numerical Methods in Fluids,2010,64(7):777-792.
[8]Malamataris N A,Löhner R.The computation of the eddy along the upper wall in the three-dimensional flow over a backward-facing step[J].International Journal for Numerical Methods in Fluids,2012,68(9):1102-1125.
[9]Malamataris N A.A numerical investigation of wall effects in three-dimensional,laminar flow over a backward facing step with a constant aspect and expansion ratio[J].International Journal for Numerical Methods in Fluids,2013,71(9):1073-1102.
[10]肖 潇,吴时强,樊新建,等.后台阶流的水动力特征[J].江苏大学学报:自然科学版,2014,35(2):149-153.Xiao Xiao,Wu Shiqiang,Fan Xinjian,et al.Hydraulic characteristics of backward-facing step flow[J].Journal of Jiangsu University:Natural Science Edition,2014,35(2):149-153.(in Chinese).
[11]Chaudhary H,Dhiman A.Two-dimensional laminar fluid flow and heat transfer over a backward-facing step:effects of reynolds and prandtl numbers[J].Heat Transfer Research,2011,42(4):379-402.
[12]孙正中,苏莫明,周 铮.平面不可压后台阶湍流流动的数值模拟:壁面温度的影响[J].航空计算技术,2009,39(4):71-74.Sun Zhengzhong,Su Moming,Zhou Zheng.Numerical simulation of 2-D incompressible turbulent flow over a backward-facing step:effects of wall temperature[J].Aeronautical Computing Technique,2009,39(4):71-74.(in Chinese)

