基于《课程标准》的中学数学试卷契合度评价
梁建梭,陈奕娟,张诚一
(海南师范大学数学与统计学院,海南海口571158)
试卷是考查学生学习状况的重要手段,更是促进教育教学循序渐进、不断提高教学质量的有效途径之一.科学实效的试卷分析评价能成为提升教师教学水准和指导学生的积极求知催化剂,因此,基于课程标准对试卷评价显得尤其必要[1],特别是基于课程标准知识点的试卷契合度的评价.
之前有很多人对于试卷评价做了很多工作和研究,也取得一定的成果,例如河北大学耿彦如写的《模糊综合评判用于高考数学试卷评价的研究》[2],通过确定评价对象,建立指标专家小组、目标层次系统和初始指标系统,再逐步简化建立新的评价指标体系.再如浙江大学韩建民的《试卷质量模糊综合评价模型的研究和建立》[3],建立了试卷难度、区分度、信度,覆盖率、试题合格率,以及峰度、偏度三级模糊综合评判模型.但基于课程标准的试卷评价相对较少,对基于课程标准知识点的试卷契合度的评价那就更少.
基于课程标准知识点的试卷契合度是指:以课程标准中要求掌握的知识点、对知识点的掌握程度、重要度、难度[4]和能力的要求为基准,评价试卷中出题情况与课程标准中所规定的要求相匹配、贴近、一致程度的测量结果描述.这是一个模糊的概念,故利用模糊数学方法来进行评价分析会更符合客观实际.因此,本文首先基于课程标准建立知识分布体系,选取“掌握程度、重要度、难度和能力要求”作为四大指标,给出了各评价因素指标的数据标准和采集方法,并应用模糊集之间的贴近度,给出了试卷的契合度评价方法.通过对评价结果的分析,寻找其原因,针对上述的现象,提出相应的政策、措施和建议.
1 模糊贴近度的相关知识
度量两个模糊集合的关系密切程度可以用两者之间的距离来描述,即距离越大,关系越稀疏;而距离越小,则关系越密切.然而当论域的元素较多时,用距离来描述,其工作量往往较大,为此,我国学者汪培庄等人提出了另一种表示两个模糊集接近程度的“贴近度”概念,具体求两个模糊集的贴近度步骤如下:
1)建立原始数据矩阵
设待分类的n个样本为{x1,x2,…,xn},每个样本都有m个特征,记为
xi={xi1,xi2,…,xim},i=1,2,…,n
于是得到原始数据矩阵:即
X=(xij)n×m,i=1,2,…,n;j=1,2,…,m.
从而可用一个描述特征的矩阵来描述整个样本集,X中的每一列代表所有样本的一种特征值,每一行代表一个样本的所有特征值.
2)数据规格化处理
为了保证研究的科学性,本文使用数据均来自2012年普通高等学校招生全国统一考试理科数学试卷(必修+选修II).由于特性指标的量纲和数量级不相同,故在运算过程中可能突出某数量级特别大的特性指标对分类的作用,而降低甚至排除了某些数量级很小的特征指标的作用,致使对各特征指标的分类缺乏一个统一的尺度.为了消除这一影响,首先对数据进行数据规格化的处理.相应的变换公式为:
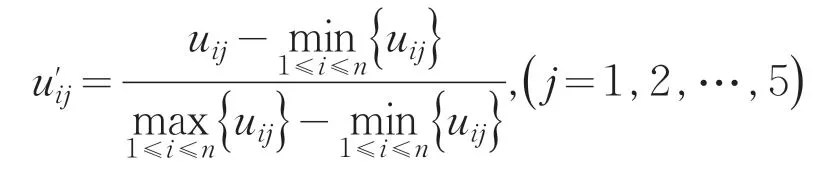
显然通过对原始数据的处理,得到初始矩阵.
3)计算模糊集合的内积与外积[5]
设U为论域,,则称(A(u)∨B(u))为A与B的内积;称A∙B=∧u∈u(A(u)∧B(u))为A与B的外积.
4)模糊集合之间的格贴近度[5]
2 基于《课程标准》的数学试卷契合度评价
2.1 建立课程标准知识体系
课程标准知识体系是指根据课程标准建立的知识体系.见表1.
根据知识体系,将指标集U分为四个层次:
第一级指标集:U={S,I,D,A},其中S:课程标准中要求对知识点的掌握程度;I:课程标准中界定知识点的重要度;D:课程标准对知识点所确定的难度;A:课程标准对知识点要求所要体现的能力.第二级因素集如下:
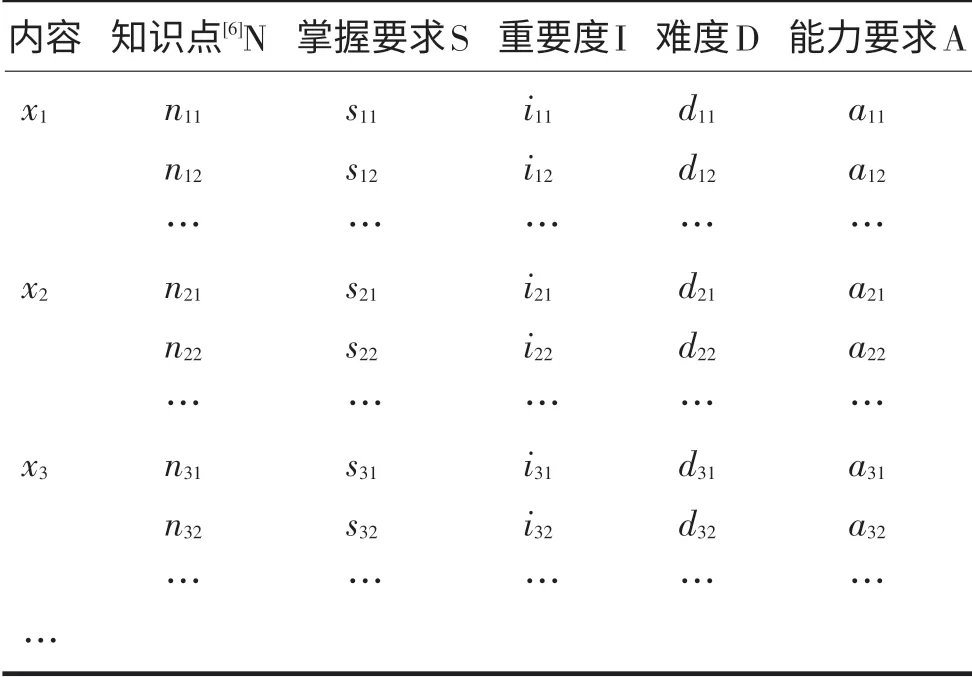
表1 课程标准知识体系Tab.1 Knowledge system of curriculum standards
1)对知识点掌握要求指标S={sij},其中sij表示知识点nij对应的掌握要求,可以根据课程标准中使用的一些行为动词,进行分类赋权值.以下是课程标准[4]中使用了一些行为动词,以界定相关内容知识点的掌握要求(见表2).

表2 课程标准要求对知识点掌握程度的分层表Tab.2 Hierarchical table about knowledge mastery of curriculum standards
2)重要度I={iij},其中iij表示知识点nij对应的重要度,用其所占课时表示;
3)难度D={dij},其中dij表示知识点nij对应的难度,同时引入史宁中教授等[8]的静态定量难度模型来计算(其中0≤α≤1),其中该模型中d表示课程难度,S表示课程深度,也用掌握知识要求深度表示,G表示课程广度,在这里指考试要求的知识点个数,T表示该课程所需要的时间,在这里也用重要度来表示,表示为可比广度,表示为可比深度,用α表示加权系数,它反映了课程对于可比广度与可比深度的侧重程度,课程难度在此实际上就是可比深度与可比广度的加权平均值.取α=0.5,因为在这里认为这两者(可比深度与可比广度)的侧重程度是相同的.
4)能力要求指标:A=(aij),其中aij表示知识点nij对应的能力要求,具体见表3.

表3 课程标准要求体现知识点的能力分层表Tab.3 Hierarchical table about reflecting the knowledge ability of curriculum standards
2.2 建立试卷知识分布体系
1)试卷体现对知识的掌握等级以及等级对应的权值,见表4;

表4 试卷要求掌握程度分等级表Tab.4 Grading table of test requiring mastery of test paper
2)试卷中知识点的重要度用其所占的分数值来衡量;
3)试卷中知识点的难度分容易、中等、较难和难三个等级,其中容易赋值1,中等赋值2,较难赋值3,难赋值4;难度越深,分数越高.
4)试卷体系中的能力要求分等级和赋值见表5.
对试卷中知识点掌握程度、难度和能力要求的确定,我们利用一线教师、考试研究人员和专家综合分析后[9]的赋值来确定.
因此,由以上的具体指标,可以建立如下试卷的知识分布体系(见表6).
3 实例应用
首先根据课程标准对知识点的分布,建立课程标准知识体系表,其次以2012年普通高等学校招生全国统一考试理科数学试卷(必修+选修II)为例,建立试卷知识分布表.最后,进行归一化处理,分别得

表5 试卷能力要求等级表Tab.5 Grading table of capacity requirements of test paper
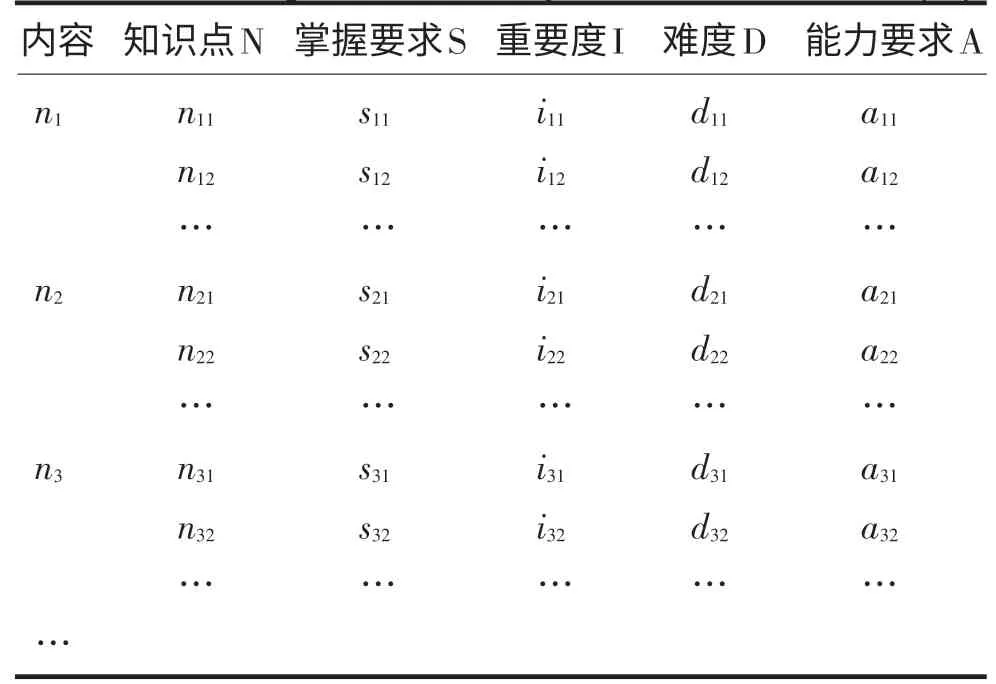
表6 试卷知识分布体系表Tab.6 Knowledge distribution system table of the test paper
到课程体系矩阵K和试卷体系矩阵F:


根据本文的需要,将选取Hamming 贴近度,即Ham⁃ming 贴近度其中.利用这种方法结果算得两体系四个指标的贴近度分别为0.7876,0.8256,0.6217,0.5532.
4 对评价结果的分析
通过分析评价结果以及相关的数据,可以进行如下分析:以函数中的对数函数知识点做例子来检验贴近度结果,课程和试卷体系中的对知识点掌握程度要求、重要度、难度和能力要求这四个指标的最初数据分别为(8/3,32/6,0.343,2)和(3,5,2,3).其中掌握程度权值分别为8/3 和3,这两个数据还是比较契合的,具体分析如下:课程体系中对数函数要求能理解①对数的概念、②掌握对数的运算性质、③掌握对数函数的概念、性质和图像,课程体系中按理解赋值2,掌握赋值3,再对对数函数这三分点加权1/3,最终对数函数掌握程度要求应该为(2+3+3)/3=8/3,掌握程度介于理解层次到掌握层次之间,而且更接近掌握层次;试卷体系中有关对数函数的题目是选择题第(9)小题,经过综合分析,我们定其要求掌握程度为掌握层次,即权值是3.重要度32/6 和5 也是相匹配的,具体分析如下:32/6表示课程体系中对数函数这个知识点所占的课时数,它占课程所有内容总课时数241的比例是2.2%,而5是表示试卷体系中对数函数知识点所占的分数,它占试卷总分数150分的比例是3.3%,两个数据还是相对接近的.知识点的难度,界定于0 到1 之间,因此0.343(34.3%)表示课程体系中对数函数这个知识点是比较容易,而2则表示试卷体系中对数函数题目(选择题9小题)的综合分析,确认其难度是中等的.能力要求数据中的2表示,在根据课程标准中对数函数的能力要求为能识别的情况下可以进一步会使用,因为权值为2;而3 表示试卷体系中对数函数考查的能力是会求会运算的层次,因此权值为3,对数函数这个知识点在能力要求上相差了一个等级.
总体上讲,四组数据还是相对贴近的,可以认为契合度比较好,其中重要度最贴近,依次到掌握程度、难度和能力要求.然而还是有一些不足,重要度分析中数据用到了所占比例来分析,而真正在计算契合度的时候并没有把比例算进去;能力要求的确定都需要人为很深入地综合分析才准确,人为的思考总会有些主观性,因此这也是不足.
计算结果表明,2012 年普通高等学校招生全国统一考试理科数学(必修+选修II)试卷的契合度是较好的.为增加契合度,本文建议:
1)单纯增加未考核到的内容,加大题目数量.同时为保证学生做题的质量,应增加相应的时间或者分段内容模式让学生进行考核,避免题目过多,学生产生厌烦的情绪.
2)删除重复知识点的题目,从而在保持题量的情况下,可以增加未包含又需要考核的知识点内容.
3)选择的题目增强综合性,知识点交叉,一题有多点,并且题目相对知识点的难度、重要度等要求需要参考课程标准中的要求来确定.
其中1)和2)点主要是提高了试卷的覆盖度[10],从而提高试卷的契合度,3)点则既能够提高试卷的覆盖度,又能使试卷对知识点掌握要求、重要度、难度和能力要求等方面更接近课程标准,从而多方面多角度改善试卷的契合度.
5 结束语
本文从课程标准的要求出发,对高考试卷的掌握程度、重要度、难度和能力要求进行分析,相应地建立了课程知识体系和试卷知识体系,进而利用模糊集之间的贴近度来计算两个体系的契合度,最后根据契合度来分析和评价试卷与课程标准的契合程度.尽管这个模型中的基本指标的构成将因不同的评价要求而改变和调整,但是模型的基本框架或形式是不变的,具有较强的普适性,也为试卷评价工作提供了一个工具参考,使得高考试卷评价更具有操作性、客观性,能在相当程度上对高考试卷能力评价起到促进作用,从而促进中学数学教育教学的发展.
[1]邓万友.综合试卷评价体系的构建与实现[J].内蒙古师范大学学报:教育科学版,2006,19(1):41-44.
[2]耿彦如.模糊综合评判用于高考数学试卷评价的研究[D].保定:河北大学,2005.
[3]韩建民,王丽侠,张玲波,等.试卷质量模糊综合评价模型的研究与建立[C].2005 年中国模糊逻辑与计算智能联合学术会论文集,2005:489-494.
[4]孙维桐.浅谈试卷分析在教学与教学管理中的作用[J].卫生职业教育,2002,20(2):87-88.
[5]谢季坚.模糊数学方法及其应用[M].武汉:华中科技大学出版社,2000.
[6]叶尧城.高中数学课程标准教师读本[M].武汉:华中师范大学出版社,2003.
[7]金晓红.基于课程标准的浙江省高考数学试卷一致性分析[D].长春:东北师范大学,2012.
[8]王辉.不同版本初中数学教科书与课程标准的一致性分析[D].长春:东北师范大学,2007.
[9]李为.一种实用于教师自评的试卷分析格式设计[J].南京晓庄学院学报,2006(1):83-87;75.
[10]朱永香,肖赞英,肖丹秦,等.试卷分析指标的选择及其应用[J].医学教育探索,2008,7(3):265-266.
——依托《课程标准》的二轮复习策略

