基于动态规划的DNA二级结构预测算法

黄鑫泉，张 凯，陈建勋

（武汉科技大学 计算机科学与技术学院，湖北 武汉430065）

0 引 言

DNA 二级结构是DNA 分子自组装［1］、DNA 计算等［1，2］纳米技术的基础，因此DNA 二级结构预测已经成为计算生物学的主要研究领域之一。DNA 二级结构预测包括基于物理化学的方法和基于生物信息学的方法两类。物理化学的方法通过X 射线结晶衍射［3］和核磁共振［4］确定DNA分子的结构，虽然预测精度高，但是对软硬件要求较高，而且DNA 分子降解较快，难以结晶，造成预测困难，所以这类方法适合于碱基数量较小的DNA 二级结构预测问题。生物信息学的方法是通过对DNA 分子二级结构的特点进行分析，通过计算机算法来预测DNA 二级结构。此类算法中，应用比较广泛的是基于矩阵的动态规划算法，该算法可以得到一个DNA 序列在给定热力学模型下具有最小自由能的二级结构，时间复杂度为O n（ ）4［5］，如果不考虑多分支环，时间复杂度可以降为O n（ ）3［6］。由于自由能函数本身的缺陷以及DNA 折叠动力学因素的影响，使得当前DNA 二级结构往往并不是处于自由能最小的状态，这就使得DNA 二级结构预测存在一个矛盾的问题：一方面我们仍然以自由能最小作为优化目标并用各种优化方法力图得到DNA 的最小自由能状态；另一方面我们耗费了大量时间和空间往往不是真实的DNA 二级结构。

本文提出的DNA 分子二级结构预测算法，是在保留当前整条DNA 分子单链中最稳定结构的前提下找出自由能在阈值范围内的稳定结构。它既考虑到DNA 分子整体结构的稳定性，即碱基对匹配数越多越稳定，又兼顾了热力学稳定性原理，即自由能越小越稳定。将实验结果与RNA structure软件结果进行对比，对比结果表明提出的新方法具有较高的准确率和覆盖范围。

1 DNA二级结构

定义1 一个长度为n 的DNA 分子序列R ＝5′－x1x2…xn－3′，其中xi∈ ｛A ，T，C，G ｝，i ＝0，1，…n。DNA 二级结构S 是碱基对 （xi，xj）的集合，其中1≤i＜j≤n，（ xi，xj）满 足：

（1）j－i＞t，其中t是小的常量值，一般取t＝3；

（2）如果 （xi，xj）和 （xi，xk）是S 的2个 碱 基对，那么j＝k；

（3）如果 （xi，xj）和 （xk，xl）是S 的2个 碱 基对，且i≠k，那么i＜j＜k＜l或i＜k＜l＜j，即不考虑虚结；

定义2 DNA 分子序列R ＝5′－x1x2…xn－3′，其中Ri，j＝5′－xixi＋1…xj－3′表示DNA 的子序列，其中1≤i＜j≤n，即R ＝R1，n。Si，j表示子序列中已匹配的碱基对，即对于任意的i≤k＜l≤j，若ρ（ xi，xj）＝1，那么（xk，xl）∈Si，j。Mi，j＝ Si，j表 示Si，j集 合 元 素 的 个 数，即子序列Si，j匹配的碱基对数。满足情况的最大碱基对匹配情况不止一只，即对于同一，子序列Ri，j有多重匹配情形，用表示所有情况的集合，即＝∪ ｛Si，j｝。

2 最大碱基对匹配算法

2.1 最大碱基匹配对数

根据DNA 二级结构特点，DNA 分子序列自身上不能太剧烈地折叠。对于一个长度为n的DNA 分子序列R ＝5′－x1x2…xn－3′，如果j－i≤t，1≤i＜j≤n（t是较小的正常熟，一般t取3），那么和就不是Si，j的碱基对，即Mi，j＝0，Si，j＝。

要计算DNA 的子序列Ri，j＝5′－xixi＋1…xj－3′，如果时，分析xj的视角考虑下面不同的情形：

（1）在最优解中，xj不与任何碱基匹配，如图1所示，在此情况下Mi，j＝Mi，j－1，Si，j＝Si，j－1。

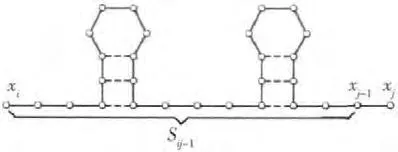
图1 情形1

（2）在最优解中，xj与xi匹配，如图2所示，在此情况下Mi，j＝1＋Mi，j－1，Si，j＝Si，j－1∪ ｛（xi，xj）｝。

图2 情形2

图3 情形3

分析比较上述3种情形，得到Mi，j的递推表达式为：

如果j－i≤t，那么Mi，j＝0。

如果j－i＞t，那么

2.2 最大碱基匹配碱基对

Mi，j的计算，可以利用动态规划算法直接迭代求解，Si，j却并不能直接计算，因为在分析Si，j的过程中，没有考虑Si，j－1、Si，k－1和的最优结构也不止一种，因此在求解出Mi，j后，分析Mi，j可能的迭代过程，从而得到满足最大碱基对匹 配的所有情况Si，j。

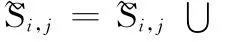
图4 DNA 二级结构

动态规划过程中，需要在求解过程中填写最有决策表结构，最有决策表是一个二维表。在计算Mi，j时，由于Mi，j是一个数值，所以存储Mi，j空间复杂度 为O （n2）。然而是一个集合，集合大小为满足Mi，j情况下的匹配情况数，在求解Mi，j的过程中，需要考虑3种不同类型，而且第3种类型中i＜k＜j－t，即集合的元素个数最多为 （j－i－t－1） ＋1＋1＝j－i－t＋1。对于，集合元素为匹配情况，也是一个集合 （集合中，每个元素为碱基对二元组），这个集合元素最多时，即每个碱基都有匹配的碱基，集合大小为。如果也用最有决策表直接填写的话， 空间复杂度为。当 DNA分子序列较长时，浪费了大量存储空间，本文使用一个O （m ）的空间记录，记为Ti，j。具 体记录方式 描述如下：初始化Ti，j＝。

（1）如果j－i＞t，如果情形1可以求解出最大碱基对数，那么Ti，j＝Ti，j∪ ｛－ 1｝ 。

（2）如果j－i＞t，如果情形2可以求解出最大碱基对数，那么Ti，j＝Ti，j∪ ｛－ 2｝ 。

（3）如果j－i＞t，如果情形3可以求解出最大碱基对数，那么Ti，j＝Ti，j∪｛k｝ 。

显然 地，Si，j与Ti，j是等价的，可以相互推导，由Ti，j迭代得到的算法描述如下：

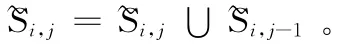
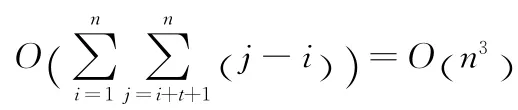
3 Nearest－Neighbor热力学模型

碱基对存在互补或不互补的4种组合：

这种基本结构可以组成各种DNA 的结构，DNA 的自由能也是这些基本结构的自由能累加得到，自由能的计算公式为

其中

本文通过最大碱基对匹配算法，动态规划求解满足最大碱基对匹配数的所有可能的二级结构，然后依据Nearest－Neighbor热力学模型计算DNA 分子所有可能二级结构的自由能，记为ΔG1、ΔG2…ΔGk（k表示满足最大碱基对匹配数的情况数），阈值为α（0.5＜α≤1），对于这k种情况，若ΔGi≥α·ΔGmax，其中1 ≤i ≤k，ΔGmax＝max｛ ΔG1、ΔG2…ΔGk｝，那么自由能为ΔGi所对应的DNA二级结构为该DNA 分子序列可能的二级结构。

接下来，分析算法的复杂性，为了计算DNA 二级结构的自由能，需要先将DNA 二级结构分解成不同的DNA 结构，时间复杂度为O （n2），然后计算各个结构之后，计算总的自由能，时间复杂度为 O （n） ，总共满足最大碱基对匹配数的情况数记为 m，那么总的时间复杂度为O （m ·n2 ）。

4 实验结果

图5 软件界面

为了验证算法的有效性，开发了XNAAPP 软件（DNA／RNA 二级结构预测计算分析系统），软件如图5所示。软件中使用的DNA 分子的Nearest Neighbor热力学参数详见文献 ［7］。为了验证算法，本文测试序列结果与RNA structure软件分析结果对比，测试序列1 为R1＝5′－CCGAACGCCGCAAAAAGCGGCGAACGCGCGAAAAACGCGCGAACGGGCGCGCCCGAACGGCGCAAAAAGCG－3′，该序列为文献［10］中使用的序列，将序列1的计算位置从49 开始，得到测试序列2 为R2＝5′－CCGAACGCCGCAAAAAGCGGCGAACGCGCGAAAAACGCGCGAACGGGCGCGCCCGA－ACGGCGCAAAAAGCG－3′。XNAAPP软 件 对 序 列1和序列2进行了分析，结果见表1，XNAAPP与RNA structure软件分析对比见表2。

表1 XNAAPP分析结果

表2 XNAAPP与RNA structure软件分析

XNAAPP 分析序列1 的最小自由能二级结构如图6所示。

XNAAPP分析序列2 的最小自由能二级结构如图7所示。

RNA structure分析序列1的二级结构如图8所示。

RNA structure分析序列1的二级结构如图9所示。

从分析结构可以看出，本文算法与RNA structure都能得到自由能最小的二级结构，对于序列1，与RNA structure所得到的DNA 分子二级结构稍有不同，本文得到的DNA 二级结构多了2个碱基对47－70，48－69，得到的结构更加稳定，明显优于RNA structure，与文献 ［14］中得到的结构是一致的，并且可以得到满足最大碱基对匹配的所有情况，共36 种，而文献 ［10］中只给出了3 种（在36种之内，包含关系）；对于序列2，与RNA struc－ture所得到的DNA 分子二级结构相同，但是如果需要包含某阈值范围内的所有DNA 分子二级结构，RNA structure软件无法实现。因此，本文算法得到的DNA 分子二级结构包含RNA structure软件得到的DNA 分子二级结构。当然，本文算法预测速度相对于RNA structure慢一些，主要表现在本文可以得到满足阈值范围内的所有DNA 分子的二级结构，而RNA structure是基于最小自由能模型得到的二级结构，只能得到自由能最小情况下的最优解。

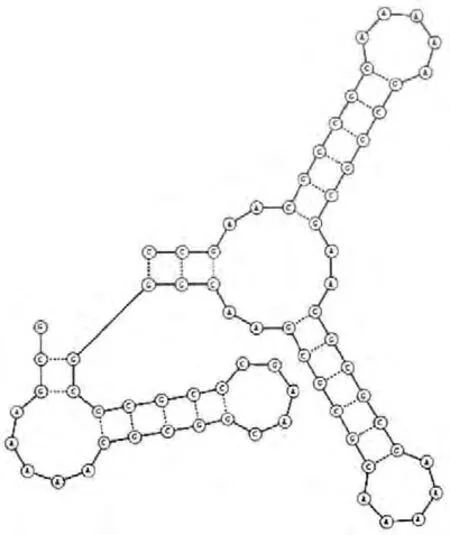
图6 XNAAPP分析序列1的最小自由能二级结构

图7 XNAAPP分析序列1的最小自由能二级结构

图8 RNA structure分析序列1的二级结构

图9 RNA structure分析序列1的二级结构

5 结束语

DNA 分子结构是生物信息学领域重要研究对象，通过DNA 结构研究病毒的遗传信息，探索DNA 参与和合成蛋白质及转录遗传信息的过程。本文给出了基于动态规划算法预测DNA 分子二级结构，可以求解得到满足最大碱基对匹配的所有二级结构，通过Nearest Neighbor热力学参数计算各种匹配下的自由能，自由能在阈值范围之类的即为可能的DNA 二级结构，然后提供给生物研究人员分析研究。实验结果与RNA structure软件结果进行对比，表明提出的新方法具有较高的准确率和覆盖范围。

本文仍然存在一些以后需要进一步研究的问题，主要在以下几个方面：

（1）从效率和准确度上综合考虑，本文算法准确度比传统算法得到的高，并且提供了多种可能的二级结构，当然，也增加了生物研究人员的工作量。从大量实验数据可以看出，算法时间复杂度出现了不确定性，主要表现在，当序列的碱基对匹配情况复杂时，会出现计算超时情况。因此在求出最大碱基对匹配情况之前，可以通过DNA 部分二级结构的自由能刷除去部分不可能的结构减少满足最大碱基对匹配的情况数，提高算法效率。

（2）另外，本文算法不能预测带假结的DNA 二级结构，关于这方面的问题，文献 ［8－10］中提出了一些解决方案，本文作者将综合考虑这些想法，看是否能够改进算法预测带假结的DNA 二级结构。

［1］LI Kenli，LUO Xing，WU Fan，et al.An algorithm in tile assembly model for maximum clique problem ［J］.Journal of Computer Research and Development，2013，50 （3）：666－675（in Chinese）.［李肯立，罗兴，吴帆，等.基于自组装模型的最大团问题DNA 计算算法 ［J］.计算机研究与发展，2013，50 （3）：666－675.］

［2］FAN Yueke，QIANG Xiaoli，XU Jin.Sticker model for maximum clique problem and maximum independent set［J］.Chinese Journal of Computers，2010，33 （2）：305－310 （in Chinese）. ［范月科，强小利，许进.图的最大团与最大独立集粘贴DNA 计算模型［J］.计算机学报，2010，33 （2）：305－310.］

［3］CHEN Sulin，SHEN Bin，ZHANG Jianguo，et al.Evaluation on residual stresses of silicon－doped CVD diamond films using X－ray diffraction and Raman spectroscopy ［J］.Transactions of Nonferrous Metals Society of China，2012，22 （12）：3021－3026.

［4］DENG Yibin，HU Bingwen，ZHOU Ping.Solid－state NMR studies of structures and molecular motions for the spidroin－like polymers［J］.Chinese Journal of Chemical Physics，2009，25（7）：1427－1433 （in Chinese）.［邓益斌，胡炳文，周平.类蜘蛛丝聚合物结构及分子运动的固体核磁共振研究 ［J］.物理化学学报，2009，25 （7）：1427－1433.］

［5］LIAO Bo，WANG Tianming.The minimum free energy algorithm for the DNA secondary structure prediction ［J］.Journal of Biomathematics，2003，18 （3）：364－368 （in Chinese）.［廖波，王天明.RNA 二级结构的最小自由能算法 ［J］.生物数学学报，2003，18 （3）：364－368.］

［6］ZOU Quan，GUO Maozu，ZHANG Taotao.A Review of RNA secondary structure prediction algorithms［J］.Acta Electronica Sinica，2008，36 （2）：331－337 （in Chinese）.［邹权，郭茂祖，张涛涛.RNA 二级结构预测方法综述 ［J］.电子学报，2008，36 （2）：331－337.］

［7］Zhang Kai，Huang Xinquan，Shi Xiaolong，et al.A dynamic programming algorithm for circular single－stranded DNA tiles secondary structure prediction ［J］.Applied Mathematics ＆Information Sciences，2013，7 （6）：2533－2538.

［8］YANG Jinwei，LUO Zhigang，FANG Xiaoyong，et al.Predicting RNA secondary structures including pseudoknots by covariance with stacking and minimum free energy ［J］.Chinese Journal of Biotechnology，2008，24 （4）：659－664 （in Chinese）.［杨金伟，骆志刚，方小永，等.基于堆积协变信息与最小自由能预测含伪结的RNA 二级结构 ［J］.生物工程学报，2008，24 （4）：659－664.］

［9］LUO Jiawei，CHEN Tao.RNA secondary structure prediction algorithm based on steam－combination ［J］.Journal of Computer Applications，2010，30 （6）：1694－1697 （in Chinese）.［骆嘉伟，陈涛.基于茎区组合的RNA 二级结构预测算法［J］.计算机应用，2010，30 （6）：1694－1697.］

［10］DONG Hao，LIU Yuanning，ZHANG Hao，et al.A method of RNA secondary structure prediction based on hidden Markov model［J］.Journal of Computer Research and Development，2012，49 （4）：812－817 （in Chinese）. ［董浩，刘元宁，张浩，等.基于隐Markov模型的RNA 二级结构预测新方法［J］.计算机研究与发展，2012，49 （4）：812－817.］