基于MCMC的改进粒子滤波算法

席志红，付存利

（哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨150001）

0 引 言

非线性、非高斯系统的状态估计问题一直是高精度机动目标跟踪领域研究的难点［1］。近年来出现了很多用于目标跟踪的非线性滤波方法，EKF［2］克服了标准卡尔曼滤波不能应用于非线性系统的问题，但EKF存在非线性系统不能够进行雅克比矩阵的求解、泰勒级数线性化只具有一阶的精度、要求噪声服从高斯分布等问题［3］。Julier等人根据确定性采样的基本思路，基于Unscented变换（UT）提出了无迹卡尔曼滤波（UKF）［4］。文献 ［5，6］已经验证采用UT 变换的方法可以获得非线性函数的二阶或二阶以上精度，滤波性能较EKF有所提高。为克服粒子滤波 （particle filter，PF）存在的粒子退化、粒子贫化、滤波精度低等缺点，本文提出了一种基于MCMC的改进粒子滤波算法即权值自适应马尔可夫蒙特卡洛无迹粒子滤波 （weight adaptive unscented particle filter－Markov chain Monte Carlo，WAUPF－MCMC）。

1 PF及其实现

PF算法是一种将递推贝叶斯统计思想与蒙特卡罗思想相结合的一种现代信号处理领域中的滤波方法。当粒子数目足够多时，修正后的经验条件分布将收敛于系统状态向量真实的条件分布，而状态向量的估计值可以通过粒子的均值近似得到。因为采用了预测和更新来自于系统概率密度函数的采样集近似非线性系统的贝叶斯估计，所以PF得到了工程上的广泛应用。

假设动态系统状态空间模型如下所示

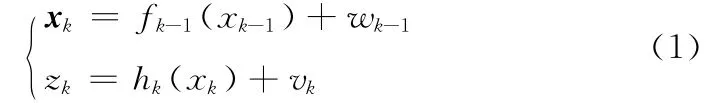
式中：fk－1（·）——系统状态函数，hk（·）——系统量测函数，xk——系统状态向量，zk——系统量测向量，wk和vk为相互独立的噪声，统计特性如式 （2）所示

式中：δkj——Kronecker－δ函数，初始状态x0与系统状态噪声wk和量测噪声vk相互独立。

标准粒子滤波的实现步骤如下：

步骤1 初始化粒子和权值

步骤2 序贯重要性采样

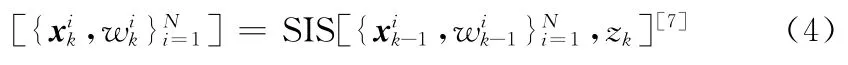
步骤3 计算粒子权值，并归一化

步骤4 重采样，得到新的粒子集合［8］。

步骤5 均值和方差的估计

PF的一个缺点是粒子退化问题，解决粒子退化的问题主要有2 种方法：一是优选重要性密度函数，例如利用EKF、UKF产生粒子滤波的建议分布函数；二是在粒子权值更新后引入重采样步骤。图1为重采样原理，上面的大小不规则的圆表示系统经过重要性采样后的粒子，圆的直径越大，代表着权值越大；下面的圆表示经过重采样后权值重新分配的粒子，重采样后所有圆的直径相同，意味着所有粒子的权值都变为1／N 。

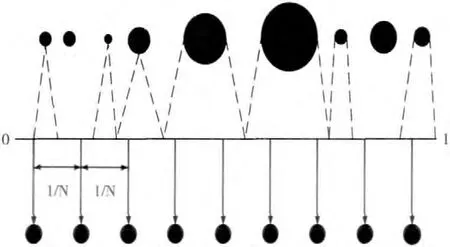
图1 重采样原理

2 MCMC在PF中的应用

针对粒子贫化问题，有效地解决方法是在重采样过程后对每个粒子引入可逆跳跃马尔可夫移动步骤，构成跳跃马尔可夫蒙特卡罗 （Markov chain Monte Carlo，MCMC）粒子滤波，即在不影响估计的后验概率分布的前提下增加重采样后粒子的多样性。典型的MCMC方法是通过搜索技术来获得函数的最大后验 （maximum a posteriori，MAP）估计，或者是在同一框架下对传统的粒子滤波算法进行多样化采样来实现的。由构造马尔科夫链方法的不同将MCMC 算法分为 MH （metropolis Hastins）和GS （Gibbs sampling）算法［9］。本文采用MH 算法，其具体的实现步骤如下：

步骤1 令v～U［0，1］。

步骤2 初始化采样分布。依照状态转移概率p（xk｜）得到粒子。

在移动判决步骤中，如果采样粒子的分布与真实后验分布相同，MCMC移动不但不会改变既定的粒子分布，还能减少粒子之间的相关性；如果采样粒子的分布脱离了后验分布，MCMC移动可能会将这些粒子移动到真实的分布区域。因此将PF算法与MCMC 方法相结合，可以有效提高粒子多样性，降低粒子的贫化问题。

3 WAUPF－MCMC及其实现

标准粒子滤波算法存在粒子退化现象，虽然重采样可以缓解这个问题，但不能从本质上解决这一缺陷，而且重采样后可能出现粒子贫化问题，使滤波的性能受到很大影响。本文提出了用UKF 算法产生粒子滤波的建议分布函数，可以将实时观测信息融入到系统中，不丢失最新观测的数据；然后改进标准粒子滤波中的权值选取和重采样这2个步骤，分别使用似然分布自适应权值调整策略和系统重采样技术；最后融入典型的MCMC 抽样算法，形成了WAUPF－MCMC算法。算法的流程如图2所示。

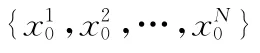
步骤2 UKF采样并进行重要性密度函数采样。使用基于比例对称方法产生Sigma点的UKF算法更新采样粒子进行状态预测，递推步骤如下所示：

（1）UT 变换。计算2n＋1个样本点以及传统计算权值的方法如下

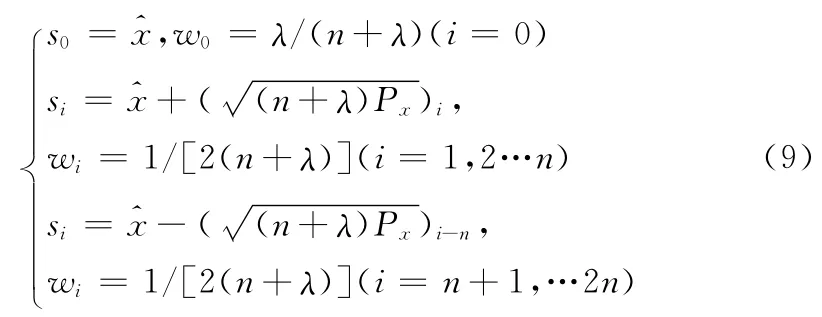
式中：px——x 的协方差，n——系统状态维数，本文采样一种基于比例对称策略产生Sigma点的方法，在权值选取方面做了改进，对应的一阶、二阶权值为

图2 WAUPF－MCMC算法流程

式中：λ＝α2（n＋κ）－n，κ——比例参数。α——比例缩放因子，可以改变α的大小来调节Sigma点到中心点的距离。β——状态向量的先验分布信息，通过合并协方差中高阶项的动差，提高协方差的近似精度。

（2）根据系统状态方程求样本点传递值

（3）求系统状态均值和方差的一步预测

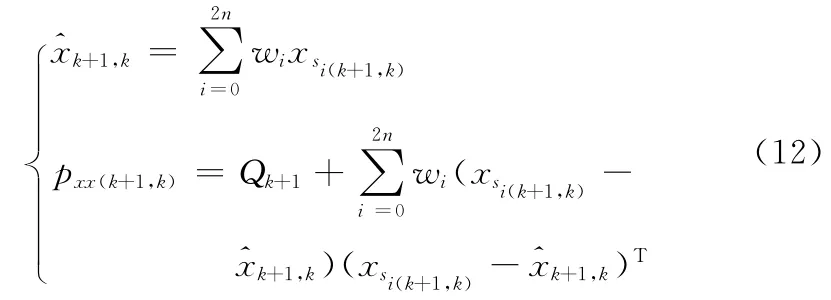
（4）根据系统量测方程求取状态一步预测的传递值

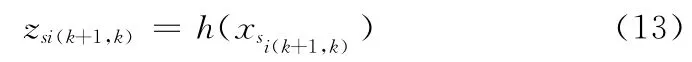
（5）获得预测量的均值和协方差

式中：pzz——量测方差矩阵，pxz——状态向量与量测向量的协方差矩阵。

（6）计算滤波增益并输出系统状态向量估计值和方差

（7）重要性采样。利用UKF更新后的数据使

步骤3 自适应权值调整并归一化：

步骤5 MCMC 步骤。根据系统状态方程，采用MH算法进行重要性采样，得到k时刻的一组预测粒子。

步骤6 令k＝k＋1，返回步骤2。

4 算法仿真与分析

对于本文提出的新算法采用典型的非线性非高斯模型来验证其有效性，该模型是非线性、非高斯系统目标跟踪中常见的模型，是研究比较各种非线性滤波的经典模型，状态方程和观测方程分别为

其中，φ1 ＝0.5，φ2 ＝0.2，φ3 ＝－2，状态方程噪声wk～Γ（3，2），观测方程噪声vk～N（0，10－5）。

文献 ［10］已经说明了在相同条件下PF－MCMC 和EPF－MCMC的滤波精度要高于EKF、UKF、PF。因此本实验采用PF－MCMC、EPF－MCMC、WAUPF－MCMC 这3种算法做比较。设粒子数N＝100，仿真时间T＝50s，采样间隔为1s，α＝1，β＝0，κ＝2，η＝0.01，初始状态x0＝1，初始方差P0＝0.75，利用Matlab2011a对3种算法进行仿真，结果如图3～图7所示。

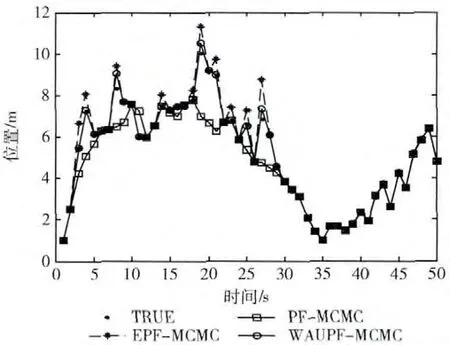
图3 3种算法跟踪

图4 3种滤波器的跟踪误差曲线

图5 PF－MCMC后验概率分布

图6 EPF－MCMC后验概率分布

图7 WAUPF－MCMC后验概率分布

图3给出真实运动目标运动轨迹与PF－MCMC、EPFMCMC、WAUPF－MCMC的跟踪曲线。图4显示了3种跟踪算法与真实轨迹的误差曲线。可见，PF－MCMC 的误差值最大，EPF－MCMC 的误差值次之，WAUPF－MCMC 的误差最小。图5～图7给出了3种滤波算法的后验概率分布情况。可以看出，EPF－MCMC 利用EKF 生成建议分布函数代替传统PF采用状态转移先验概率作为建议分布，改善了滤波效果，WAUPF－MCMC 利用UKF 生成建议分布函数，在此基础上融入 MCMC 步骤，滤波效果得到更好改进。

为了比较PF－MCMC、EPF－MCMC、WAUPF－MCMC这3种算法的性能，经50次独立仿真实验，对比3种算法的均方根误差 （RMSE），计算方法为

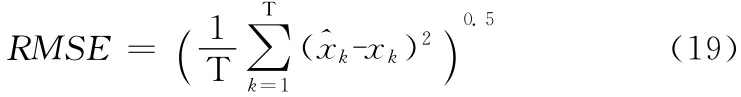
表1 3种算法性能比较

从表1可以看出，当粒子数N＝100时3种算法滤波精度相对于N＝50时均得以提高，但相应计算耗时增加。当粒子数相同时，3 种算法中PF－MCMC 计算耗时最少，但RMSE最大，不能满足高精度滤波的要求；EPF－MCMC 在滤波精度和耗时两方面都没有明显的优势；WAUPF－MCMC的RMSE最小，但耗时较多。随着计算机硬件水平的不断提高，以及可以根据具体的滤波精度要求相应的减少粒子数目和优化程序来解决WAUPF－MCMC 的实时性问题。因此，WAUPF－MCMC估计状态能够更好的吻合真实轨迹，在非线性、非高斯场合的估计性能较优。

5 结束语

近年来，PF由于自身理论上的一些优势，在解决非线性、非高斯目标跟踪问题得到广泛应用，但是粒子退化仍是尚待解决的难题。虽然重采样可以缓解这个问题，但不能从本质上解决这一缺陷，而且重采样后可能出现粒子贫化问题，使滤波的性能受到很大影响。本文从解决粒子退化、粒子多样性丧失、提高算法滤波精度等角度出发，提出了一种新型的改进粒子滤波算法即WAUPF－MCMC 算法。仿真实验结果表明，WAUPF－MCMC 的滤波精度明显高于PF－MCMC和EPF－MCMC及传统的非线性滤波器。

［1］YU Xi，ZHANG Tianqi，BAI Juan，et al.Improved algorithm of particle filtering ［J］.Computer Engineering and Design，2012，33 （10）：4010－4014 （in Chinese）.［余熙，张天骐，白娟，等.改进的粒子滤波算法 ［J］.计算机工程与设计，2012，33 （10）：4010－4014.］

［2］XIA Nan，QIU Tianshuang，LI Jingchun，et al.A nonlinear filtering algorithm combining the Kalman filter and the particle filter［J］.Acta Electronica Sinica，2013，41 （1）：148－152（in Chinese）.［夏楠，邱天爽，李景春，等.一种卡尔曼滤波与粒子滤波相结合的非线性滤波算法 ［J］.电子学报，2013，41 （1）：148－152.］

［3］Arasaratnam I，Haykin S.Cubature Kalman filters ［J］.IEEE Trans Automatic Control，2008，54 （6）：1254－1269.

［4］REN Fujun，ZHANG Xiuhua，JIANG Yongcheng.Applica－tion of an improved UKF algorithm in mobile－robot localization system ［J］.Journal of Harbin Engineering University，2012，33 （10）：1289－1294 （in Chinese）. ［任福军，张秀华，姜永成.改进UKF算法在移动机器人定位系统中的应用 ［J］.哈尔滨工程大学学报，2012，33 （10）：1289－1294.］

［5］Kim J，Vaddi S S，Menon P K，et al.Comparison between nonlinear filtering techniques for spiraling ballistic missilestate estimation ［J］.IEEE Transactions on Aerospace and Electronic Systems，2012，48 （1）：313－328.

［6］SUN Jingle，TANG Linbo，ZHAO Baojun，et al.A new particle filter tracking algorithm based on rayleigh distribution［J］.Journal of Electronics ＆Information Technology，2013，35 （4）：763－769 （in Chinese）. ［孙景乐，唐林波，赵保军，等.基于瑞利分布的粒子滤波跟踪算法 ［J］.电子与信息学报，2013，35 （4）：763－769.］

［7］Zhan R，Xin Q，Wan J.Modified unscented particle filter for nonlinear Bayesian tracking ［J］.Journal of Systems Engineering and Electronics，2008，19 （1）：7－14.

［8］Scharcanski J，Oliveira A B，Cavalcanti P G，et al.A partclefiltering approach for vehicular tracking adaptive to occlusions［J］.IEEE Transactions on Vehicular Technology，2011，60（2）：381－389.

［9］Assheton A，Hunter A.A shape－based voting algorithm for pedestrian detection and tracking ［J］.Pattern Recognition，2010，44 （5）：1106－1120.

［10］LU Chuanguo，FENG Xinxi，ZHANG Di，et al.Monte Carlo Markov chain cubature particle filter ［J］.Journal of University of Electronic Science and Technology of China，2012，41 （6）：859－864 （in Chinese）. ［鹿传国，冯新喜，张迪，等.马尔可夫链蒙特卡罗容积粒子滤波器 ［J］.电子科技大学学报，2012，41 （6）：859－864.］