基于最小二乘支持向量机的瓦斯涌出量预测模型

张幸幸 苗 星

(河南师范大学 计算机与信息工程学院，河南 新乡 453007)

0 引言

依据我国煤矿瓦斯涌出量分类的统计数据，高瓦斯矿井占35%，这些高瓦斯矿严重威胁着采煤工作面的安全。瓦斯涌出量的准确预测对于通风系统的设计、瓦斯防治、安全管理有着重要意义。我国从20世纪50年代就开始进行这方面的研究，例如矿山统计法、分源预测法、构造单元分源预测法等[2-3]。

随着现代技术的迅速发展，特别是数学方法和计算机技术的发展，原有的预测方法和应用范围得到了拓展，出现了一些新的预测方法，如瓦斯地质数学模型、速度预测法、灰色系统理论、神经网络等，但这些方法还在探索阶段。而近年来新兴的支持向量机(support vector machine，SVM)可以为瓦斯涌出量预测提供极大地便利[2]，本文首先利用GA 对LS-SVM 中的相关参数进行优化，然后利用LS-SVM 对瓦斯的影响因子进行训练，进而对瓦斯涌出量进行预测。对比BP 神经网络的预测结果，基于该方法的瓦斯涌出量预测模型具有较高的预测精度，为工程应用奠定了基础。

1 遗传算法优化参数的原理

遗传算法是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法,能够在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最优解。

用遗传算法优化LS-SVM 参数过程如下[4-5]:

Step 1 :设置初始值,如遗传算法的初始种群规模、最大遗传代数T、交叉概率、变异概率等。

Step 2 :对要优化的参数根据其设定的范围进行二进制编码,随机产生初始种群。染色体为各参数二进制顺序排列组成,长度即为各参数二进制长度之和。设置遗传代数计数器t=0。

Step 3 :计算种群中各个个体的适应度。这里将最小二乘支持向量机的预测正确率作为目标函数值,即个体的适应度,个体对应的参数的预测正确率越高,则该个体的适应度越大。

Step 4 :根据个体适应度,按照一定规则(这里采用轮盘赌法)从当前种群中选出个体进入下一代。

Step 5 :选择群体中的两个个体x1、x2 作为父体以某个概率 (交叉概率)进行交叉操作,产生两个新个体。这里采用单点交叉,交叉概率设为0.8。

Step 6 :随机选择种群中的个体以一定的概率(变异概率)进行变异操作,通过随机改变个体中某些基因而产生新个体。变异概率设为0.05。

Step 7 :终止条件判断。若t≤T,则转到步骤2；若t＞T 或平均适应度值变化持续小于某一常数超过一定代数,则所得到的具有最大适应的个体作为最优解输出,算法终止。

Step 8 :对得到的最优解译码,得到优化的参数。

2 最小二乘支持向量机的预测原理

SVM[6-8]是一种全新的和强有力的分类和回归工具，标准的SVM算法是将一个实际问题转化为一个带不等式约束的二次凸规划问题，而LS-SVM 是将实际问题转化为求解一组线性方程组的问题，简化了计算，提高了收敛速度。其具体回归算法如下[6]：

对于给定的训练数据集s={(x1，y1)，(x2，y2)，...，(xl，yl)}∈Rn×R，利用如下高维特征空间的线性函数来拟合样本集：

f(x)=wTφ(x)+b

式中：φ(x)为输入空间到高维特征空间的非线性映射；w 为特征空间权系数向量；b 为偏置。根据结构风险最小化原理，LS-SVM 回归可以表示为如下约束优化问题：

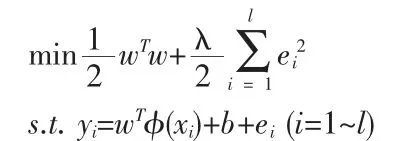
为了求解上述优化问题，需将约束优化变为无约束优化。引入拉格朗日函数，将目标函数的优化问题变换到对偶空间，则

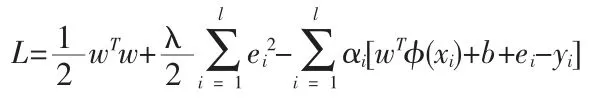
式中：αi为拉格朗日乘子；λ 为常数；根据KKT (Karush-Kuhn-Tucker)条件，则∂L/∂w=0，∂L/∂b=0，∂L/∂ei=0，∂L/∂αi=0，即

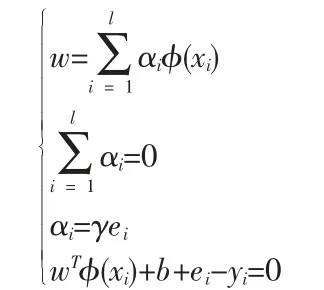
对于此式，消去w 和ei可得到如下线性方程组：

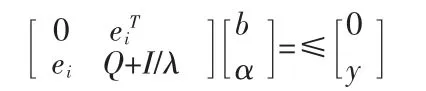
式中：ei=[1,...,l]T；α=[α1,...,αl]T；y=[y1,...,yl]T；Q=φ(xi)Tφ(xi)；根据Mercer条件定义核函数k(xi,xj)=φ(xi)Tφ(xi)。

利用最小二乘法求解上线性方程组，从而解出a 和b，最后得到LS-SVM 回归函数：

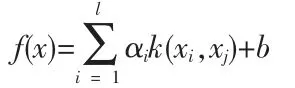
从线性方程组可以看出，只有参数λ 是待选的，这比标准SVM 待选的参数少，不再需要指定收敛判据的精度。所以LS-SVM 算法运行简单，速度快，精度高。

3 实验仿真

仿真运用的实验平台为Windows 8，4G 内存，软件为MATLAB(R2013a)。某煤矿回采工作面瓦斯涌出量与影响因素统计表如表1 所示，其中煤层深度(m)、煤层厚度(m)、煤层瓦斯含量(m3·t-1)、煤层间距(m)、日进度(m·d-1)、日产量(t·d-1)分别表示为x1～x6，x0为瓦斯涌出量。

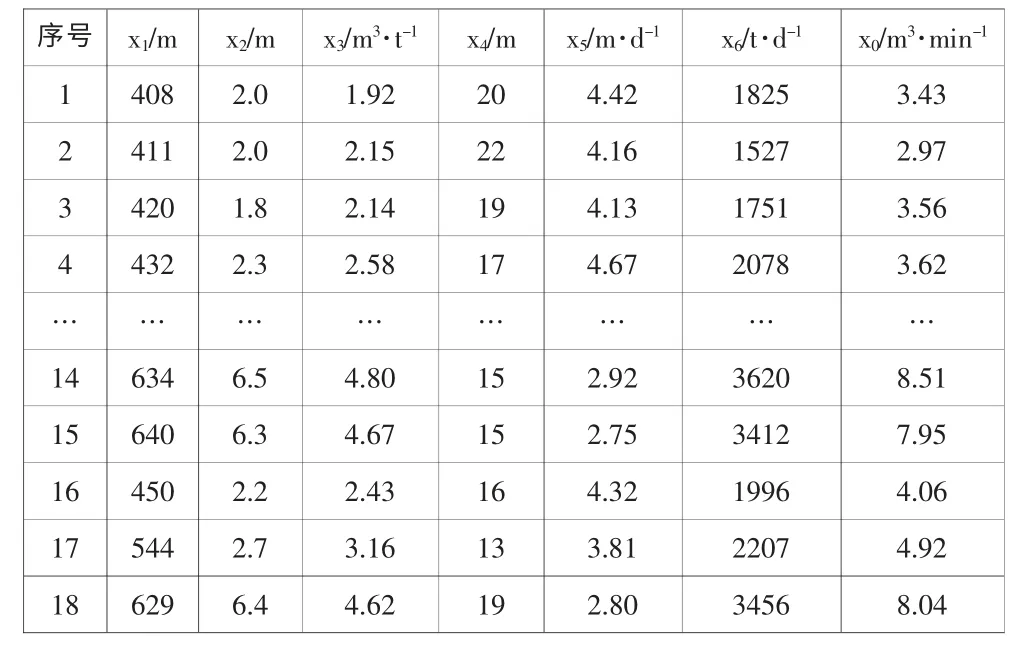
表1 瓦斯涌出量与影响因素统计表(部分)

用前13 组数据作训练样本，其中x1～x6是训练样本集，x0是训练目标集，则得到基于LS-SVM 的瓦斯涌出量预测模型，模型中的参数用GA 优化后，惩罚系数C=165.63，μ=63.85。最后用第14-18 组数据中x1～x6作为测试集，训练出瓦斯涌出量x0。同时用神经网络预测第14-18 组数据中的瓦斯涌出量x0[9-10],目标收敛趋势如图1 所示，实验预测结果及两类预测值与表1 中实际值的绝对误差如表2 所示，二者的平均绝对误差分别是0.1847 和0.3040，则LS-SVM 对瓦斯涌出量的预测效果明显比神经网络好。

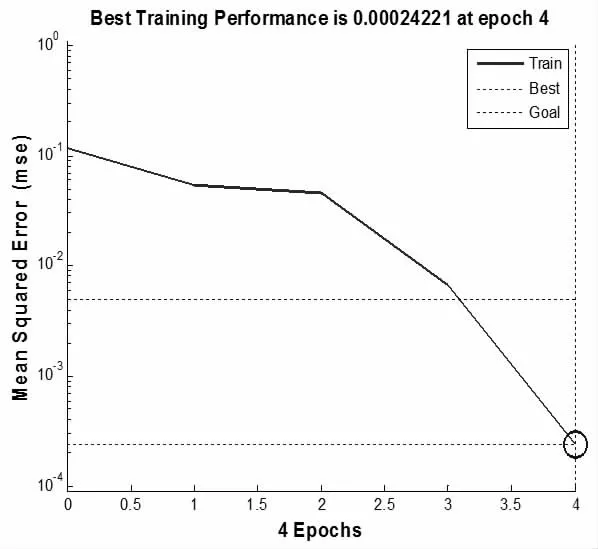
图1 神经网络训练目标值的变化趋势

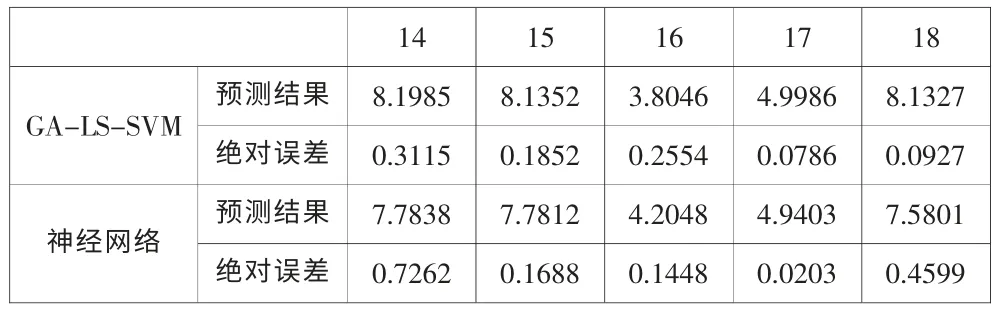
表2 第14-18 组瓦斯涌出量预测结果与误差

4 结束语

本文将基于统计学习理论的LS-SVM 和GA 应用到煤矿瓦斯涌出量的预测研究中，用GA 对LS-SVM 的相关参数进行优化，然后用LS-SVM 进行预测。与神经网络预测的结果相比，LS-SVM 的预测结果更精确，与实际值的误差更小，训练速度更快，对进一步解决实际工程问题具有很好的应用前景。

［1］章立清，秦玉金，姜文忠，等.我国矿井瓦斯涌出量预测方法研究现状及展望[J].煤矿安全，2007，393(8):58-60.

［2］梁华珍.工作面瓦斯涌出量预测的研究与应用[D].安徽:安徽理工大学，2007，06.

［3］王一莉.瓦斯涌出量预测方法及其应用研究[D].南京：南京工业大学，2005，05.

［4］雷英杰，张善文，李续武，等.MATLABGA 工具箱及其应用[M].西安：西安电子科技大学出版社，2005.

［5］王克奇，杨少春，戴天虹，等.采用GA 优化最小二乘支持向量机参数的方法[J].计算机应用与软件，2009，26(7):109-111.

［6］王晓兰，王明伟.基于小波分解和最小二乘支持向量机的短期风速预测[J].电网技术，2010，34(1):179-184.

［7］朱家元，杨云，张恒喜，等.基于优化最小二乘支持向量机的小样本预测研究[J].航空学报，2004，25(6):565-568.

［8］叶徐静.基于最小二乘支持向量机的风电功率超短期预测[J].电源学报，2013(2):30-35.

［9］彭望蜀.基于BP 神经网络与支持向量机的股票指数预测模型比较[J].金融市场，2013(437):71-73.

［10］聂勋科.基于神经网络的污水出水COD 预测模型[J].重庆工学院学报：自然科学，2008，22(8):156-162.