变系数统计模型研究进展

张辉国

（新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830046）

线性回归模型是分析变量间相依关系的强大统计方法，被广泛应用于众多领域。Hastie 和Tibshirani[1]通过设定线性模型的参数为某些协变量的非参数函数，提出了变系数模型（varying coefficient models）用于探索高维数据回归结构的动态模式。变系数模型极大扩展了经典线性回归模型，此后近二十年内，变系数模型被深入研究，并被应用于许多学科领域，如环境科学、生态学、计量经济学、金融学和医学等[2]。

1 变系数回归模型及其研究进展

变系数模型一般形式可表示为：

其中，Y 表示响应变量，而X1,X2,…,Xm和U 表示协变量，误差ε 满足E(ε｜U，X1,…,Xm）=0 和Var(ε｜U，X1,…,Xm）=σ2(U),βj(U)(j=1,2,…,m)是关于U 的一些未知非参数函数。此外，当设定X1=1 时，模型将包含一个变截距项。

变系数模型兼具线性回归模型良好的解释性和非参数回归模型的灵活性，在探索回归关系动态特征方面是一个强有力工具。变系数模型能够显著减少模型设定的偏误（modeling bias），并且能有效避免“维数灾难”[3]（curse of dimensionality）。因其良好的适应性和解释能力，变系数模型被用于分析纵向数据（longitudinal data）、函数型数据（functional data）、生存数据（survival data）以及时间序列（time series data）等。此外，以变系数模型为基础还发展了一系列有着广泛应用背景的衍生模型，包括广义变系数模型和半变系数模型 (semi-varying coefficient models)等。关于变系数模型的统计推断理论及其在众多学科领域的实际应用可参见Park 等的综述[4]。

变系数模型将回归系数估计的变化特征作为反映解释变量与响应变量动态关系的主要证据。因此在变系数模型统计推断的研究中，两个检验问题极其重要：

1）变系数模型中的系数函数是否真的变化？亦即需要检验模型系数是否为常数；

2）如果某个系数是变化的，那么它是如何变化的？ 亦即需要探索系数函数变化的细部特征，例如函数的单调性、凹凸性、峰值、谷值和拐点等变化特征。

大量研究工作都致力于解决第一个问题，如关于系数估计的逐点置信区间（pointwise confidence intervals）以及邦弗伦尼置信带（Bonferroni-type confidence bands）的研究以及关于变系数模型和广义变系数模型系数估计的联合置信带（simultaneous confidence band）的研究[5]。此外，还提出了利用拟合优度方法（goodness-of-fit tests）检验变系数模型系数是否为常数。若利用以上方法检验确认变系数模型的某个系数是显著变化的，那么进一步探索该系数变化的细部动态特征在应用中是非常重要的。然而，目前鲜见针对此主题，即上述第二个统计推断问题的研究工作。

由于变系数模型是局部线性模型，因而使用核光滑方法（kernel smoothing method）拟合模型是非常适宜的。在此情形下，上述针对变系数模型的两个关键统计推断问题都要面临非参数核光滑方法中重要而困难的问题：如何选择最优带宽或合适的光滑水平。带宽水平会直接影响回归系数估计和推断结果，尽管有一些经验性的准则用于选择带宽，但带宽选择问题始终没有满意的解决方法。例如，交叉验证方法（cross-validation，CV）、施瓦兹信息信息准则（Schwarz information criterion，SIC）和赤池信息准则[6](AIC)。研究发现，若变系数模型的各个系数具有不同光滑度（degrees of smoothness）时，情况将变得非常复杂，因为要得到不同光滑度系数的有效估计，必须对各个系数选择不同的带宽水平，高光滑度系数函数需要较大的带宽水平，而低光滑度系数则需要较小的拟合带宽。然而实现这一操作并不容易，主要原因在于缺乏各个系数光滑度的具体信息，因此不得不在多个带宽水平下，采用分步拟合方法[7]。事实上以系数估计为目的而选择的最优带宽水平并一定适合假设检验的需要。不同光滑度的系数在不同光滑水平下被分别估计，这使得为每个系数的统计检验选择一个适宜的光滑水平变得更加困难。变系数模型被视为探索变量间回归关系的重要工具，应用于众多学科领域，但是变系数模型系数估计和统计推断却始终被“最优带宽选择”和“系数具有不同光滑度”等问题困扰。此外，前述文献中所涉及的检验方法主要从全局角度检验系数是否变化，而不能充分探索那些变化系数函数的细部变化特征。因此，有必要发展新的变系数模型推断方法用于分析系数函数显著的动态变化特征，如系数函数的单调性、峰值和谷值等，这在实际应用中是不可或缺的。

另外一个值得关注的问题是变系数模型的稳健推断方法，若数据集存在异常值，它们会在回归系数函数估计中创造出虚假的回归关系特征，这可能会误导探索高维数据回归结构的动态模式。许多方法先后被研究用于变系数模型的估计，如核方法，样条方法，局部多项式方法，局部极大似然方法以及联合置信带[5]等。上述方法大都基于均值回归，使用最小二乘方法得到系数估计。众所周知，若数据有厚尾特征或数据包含异常值时，系数估计会缺乏稳健性，最小二乘法将不再是适宜的拟合方法，因为异常值会扭曲模型拟合过程，在系数估计中创造出虚假变化结构。尽管一些稳健方法用于变系数模型估计，包括L1 估计，M 估计，分位数回归，上述研究除了给出系数函数的稳健估计还建立了相应的逐点置信区间，但是这些方法难以满足实际应用。

2 空间变系数回归模型及其研究进展

在地理、环境、气象、生态、经济、金融、人口以及流行病等众多学科领域的科学研究中，研究对象的观测数据总是在特定的地理空间位置被搜集整理，形成了具有空间位置属性的空间数据集，例如某区域内的气象数据、环境监测数据、流感病例数据或经济数据等。因其广泛的应用前景，伴随着近年计算机运算能力的进步和各领域空间数据生产能力的提升，空间数据统计分析方法正成为统计学新兴分支学科--空间统计学研究的前沿热点，空间数据分析方法与某些学科的交叉甚至产生了诸如空间生态学、空间计量经济学等一些特色鲜明的交叉学科[8]。

回归分析是分析变量间相依关系的强大统计方法，然而经典的回归模型却无法直接应用于空间变量间相依关系的分析，原因在于时空数据的两个基本统计特性：空间数据的自相关性和空间数据的非平稳性。空间数据的这些特殊属性违背了经典回归分析得以有效应用的重要前提假设。自二十世纪九十年代，对空间数据自相关性和非平稳性建模研究过程中，Fotheringham 等人[9]基于变系数模型提出了如下空间变系数地理加权回归(geographically weighted regression，GWR)模型

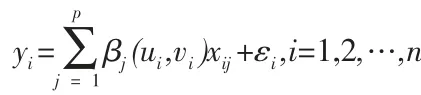
其中，(ui,vi)是研究区域内第i 个位置的空间坐标，(yi;xi1,…,xip)为响应Y 变量和解释变量X1，X2，…，XP在空间位置（ui,vi）处的观测值；βj(u,v)(j=1,2,…，p)是待估回归系数函数；εi(i=1,2,…，n)是相互独立服从正态分布的随机误差，且满足期望为零，方差为σ2。另外，若假定xi1≡1(i=1,2,…，n)，上述模型将包含一个空间变化的截距项。

空间变系数模型克服了全局回归模型不能有效分析空间数据自相关性及回归关系空间非平稳性的不足，被广泛用于分析空间数据非平稳特征，是探索回归关系空间非平稳性的有效工具，在众多学科领域中涌现出大量相关应用研究成果。近几十年来，地理加权回归不仅在诸如地理学、环境科学、生态学和计量经济学等众多领域内有大量应用性结果，同时在统计推断和理论方法改进方面也不断涌现新成果。地理加权回归、混合地理加权回归的假设检验问题、共线性和变量选择问题以及异方差问题均得到细致的研究。最近的实证研究在地理加权回归分析框架探讨了空间多尺度非平稳性以及回归关系的尺度依赖性质[10]。

空间变系数模型的系数估计曲面被当作探索和解释回归关系的空间非平稳性的主要证据，因此系数估计准确性及其统计检验对于得到回归关系结构的正确结论非常重要。无论地理加权回归估计还是统计检验都面对一个棘手的问题：选择一个最优带宽或一个合适的光滑水平。众所周知，带宽的水平对于回归系数的估计和统计推断有很大的影响，而且到目前为止，地理加权回归方法中的带宽选择问题始终没有一个满意的解决方案，尽管有一些诸如交叉验证以及校正AIC 准则[9]等选择带宽的数据驱动方法，但是此类数据驱动方法与响应变量的观测值密切相关，这使得推导检验统计量的精确分布变得非常困难。另一方面，以系数估计为目标选取的带宽未必适合统计检验，因此为了确定带宽变化对统计检验稳健性的影响应当在一个较大带宽范围内实施统计检验。如果空间变系数模型的系数函数具有不同光滑度，那么就不可能存在某个单一带宽作为所谓最优带宽而适合所有系数估计，因为在估计高光滑度系数函数时需要较大带宽值，而估计 低光滑度系数函数时则需要较小带宽水平。由此可见，受到带宽选择问题的影响，单一带宽水平下地理加权回归系数估计所反映的回归关系的空间变异模式是不可靠的。需要强调的是上述检验方法中所使用的检验统计量都是全局统计量，根据全局统计量检验结果可以推断回归系数在整个研究区域内是否变化，但是当系数为常数的原假设被拒绝后却无法进一步推断出系数函数在研究区域内变化的细节特征。

空间尺度问题是研究空间变量相依关系过程中必须要考虑的因素。长期的空间数据统计分析研究实践发现，空间数据统计特征与研究者所限定的空间范围密切相关，如空间自相关性、非平稳模式和空间数据异常值探测（SOD,spatial outlier detecting）过程会随数据的空间尺度而变化。空间数据统计特征的尺度相依性（scale dependence）严重制约了各种经典统计方法探索分析时空数据的有效性，为时空数据统计分析研究带来巨大挑战，指出空间局部模型为分析具有尺度相依性的各种空间数据特征开辟了极具研究价值的新途径。大量研究结论亦证实回归关系的空间变异通常与空间尺度相关，即具有尺度相关性。上述研究指出地理加权回归所使用的核函数中的带宽参数实质上空间尺度的某种测度。因此，仅使用单一的带宽值不能准确估计具有不同光滑度的系数函数，并且也不能充分探索回归关系中具有尺度相依性的空间变异。基于上述原因，有必要转变传统的观点：从选择某个最优带宽值用于估计潜在的真实回归系数的观点转向在不同尺度或光滑水平下全面考察回归关系。

在地理加权回归分析中，变系数模型的系数估计的变化模式被看作探索回归关系非平稳特征的主要证据。因此，探索系数估计所具有的空间变化模式并对这些变化特征实施统计显著性检验是得到空间回归关系非平稳特征的真实结论的先决条件。从非参数回归拟合方法角度看，传统的地理加权回归和局部线性地理加权回归均以核光滑方法为基础，它们利用局部加权最小二乘方法估计模型中的回归系数函数。然而，最小二乘方法对于异常值是不稳健的，地理加权回归方法也因此会扭曲空间变系数模型的估计过程。事实上，数据集特别是大型数据集中通常都会存在异常值，它们会在系数函数估计中创造出虚假的回归关系结构特征，这会误导回归关系非平稳性的探索结论。由于在地理加权回归方法中，回归系数估计为局部估计，最终探测到的异常值也相应为局部异常值，准确探测异常值并不容易。然而局部异常值不一定是全局异常值，并且也不一定是有问题的数据，所以应当谨慎对待异常值，而不是简单地丢弃它们。因此针对空间变系数模型发展能处理异常值的稳健的拟合与推断方法是有价值的研究方向。

［1］Hastie TJ,Tibshirani RJ.Varying-coefficient models [J].Journal of the Royal Statistical Society B,1993,55:757-796.

［2］Fan J,Zhang W.Statistical methods with varying coefficient models [J].Statistics and Its Interface,2008,1:179-195.

［3］Fan J,Zhang JT.Functional linear models for longitudinal data [J].Journal of the Royal Statistical Society B,2000,62:303-322.

［4］Park BU,Mammen E,Lee YK,Lee ER.Varying coefficient regression models:a review and new developments[J].International Statistical Review,2014,82:1-19.

［5］Zhang W,Peng H.Simultaneous confidence band and hypothesis test in generalized varying -coefficient models [J].Journal of Multivariate Analysis,2010,101:1656-1680.

［6］Cai Z,Xu X.Nonparametric quantile estimations for dynamic smooth coefficient models [J].Journal of the American Statistical Association,2009,104:371-383.

［7］Fan JQ,Zhang WY.Two-step estimation of functional linear models with applications to longitudinal data [J].Journal of the Royal Statistical Society B,2000,62:303-322.

［8］Nelson TA.Trends in spatial statistics [J].The Professional Geographer,2012,64:83-94.

［9］Fotheringham AS,Brunsdon C,Charlton ME.Geographically Weighted Regression:The Analysis of Spatially Varying Relationships[M].Chichester:Wiley,2002.

［10］Su S,Xiao R,Zhang Y.Multi-scale analysis of spatially varying relationships between agricultural landscape patterns and urbanization using geographically weighted regression [J].Applied Geography,2012,32:360-375.