循环预冷气液两相流压降特性及引射气等效研究
陈士强 范瑞祥 黄 兵 黄 辉
(1北京宇航系统工程研究所 北京 100076)
(2中国运载火箭技术研究院 北京 100076)
1 引言
循环预冷是低温液体运载火箭动力系统广泛采用的射前预冷方案,从而有效地实现节省推进剂预冷消耗量、增加预冷安全系数。低温动力系统循环预冷方案主要采用不增压下的自然循环预冷和增压下的引射循环预冷。自然循环预冷是利用外界换热使回流管路中出现汽化而密度降低,通过管路中的密度差形成的压差驱动流动;引射循环预冷则是在气枕增压导致自然循环预冷受抑制时,通过主动注入气体造成回流管路内流体密度减小,实现在循环回路上建立密度差、形成循环压差,并附加引射作用,保证预冷的正常进行。由于引射气质量流量较小,气液间动量交换和引射作用相对较弱,引射气对循环管路驱动力的贡献主要为增大密度差。
由于低温推进剂与管壁换热汽化及主动注入气体,循环预冷上升段管路内形成气液两相流动,其压降特性成为引射循环预冷系统重要特性参数之一,直接决定系统驱动力,影响循环预冷系统的设计,这点对空间应用意义更为重大。氦气是引射循环预冷系统中普遍采用的引射气工质,但是由于其价格昂贵且不可回收,使得系统级实验花费非常高。有效地探索不同引射气间压降等效关系,在实验中用价格低廉的氧气模拟氦气作为引射气对工程实践很有意义;同时,可以采用同种工质间的气液两相仿真研究代替含有不可冷凝气体(如氦气)的三相系统仿真,大幅度降低数值模拟工作难度,更好地为工程实践提供参考。
2 管路气液两相流模型
在管路流动特性计算中,控制方程为流体力学基本方程组。对于两相流动,一般对各相列出各自的守恒方程,同时还应考虑两相间的相互作用。各国学者在处理这种气液复杂共流时,常作某些假设,使问题简化,通常采用以下3种模型化方法。
(1)均相模型:是把气液混合物看成为一种均匀介质,因此可以把气液两相管路当作单相管路处理。均相模型基于如下两个假设:气相和液相的速度相等,管路由此还具有截面含气率和体积含气率相等、气液混合物流动密度和真实密度相等等特点;气液两相处于热力学平衡状态,相间无热量传递,流动介质的密度是压力的单值函数。
(2)分相模型:把管路内气液两相流动看作是气液各自分别的流动,存在两个假设:气液两相有各自的按所占流通面积计算的平均速度;气液两相间可能有质量的交换,但气液两相介质处于热力学平衡状态,相间无热量传递。
(3)流型模型:首先根据两相流动参数分析得到两相流流型,然后按各种流型的特点,分析其流动特性并建立关系式,这种处理方法称流型模型。流型模型可以更深入地揭示两相流各种流型的流体力学特性。目前,在工程上使用的流型模型经验关系式大部分是依据特定实验数据确立的各种流型。
3 管路气液两相流压降计算方法
管路气液两相流压降分为加速压降、重力压降和摩擦压降3部分:
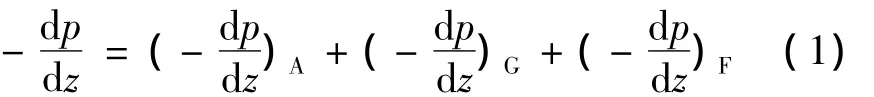
式中:d p为d z管路内流动介质的绝对压力降,z为管路长度。
3.1 加速压降
一般可以将计算气液两相流加速压力降的关系式分为两类:均相模型和分相模型。在分相模型中,需要考虑气液两相之间的相对速度。
根据两相流动基本方程,对于恒定截面的管内稳态气液两相流动,其加速压力梯度可以写为:

式中:G、A、U、x、υ、α 分别为质量流量、流通面积、速度、干度、比容和截面含气率。
3.2 重力压降
根据两相流动基本方程,重力压力梯度可以写为:

3.3 典型气液两相流摩擦压降计算模型
摩擦压降是管路气液两相流压降中最为复杂也最重要的一部分,由于机理的复杂性,相关理论分析和经验关系式并未得到普遍认可,文献报道了大量的针对具体工况或具有一定普适性的经验或半经验关系式[1-7]。
3.3.1 LMC 关系式
LMC模型(Lockhart-Martinelli-Chisholm)是一种常用的摩擦压降预测模型。该方法的基本出发点是两相管路中气液两相无相互作用,即把两相管路假想成由两条分别输送液体和气体的单相管路组成,并由两条假想管路的压降推导出与真实两相管路的压降关系。该方法是早期气液两相摩擦压降计算方法,后期研究表明,由于折算系数与截面含气率的关系曲线取自小管径实验数据,使得该法仅能用于管径较小、气液比不高的管路,且随管径的增大其计算误差增加。
3.3.2 Dukler I关系式
气液两相流动摩擦压降模型中最简单的一类模型为均相流动模型。均相模型假设气液两相介质形成一种等效的均匀混合物,具有某种均匀混合物的密度、粘度和速度,相互之间无滑动,可以利用单相流摩擦压降关系式来计算相应的两相流摩擦压降,即达西公式:

式中:D为管路内径,Um为气液混合物速度,ρm为气液混合物密度,fm为两相混合输运摩擦阻力系数,可以按照单相流关系计算:

式中:Rem=ρmUmD/μm为两相雷诺数。参数 C和n依赖于流动状态,对于湍流,C=0.079,n=0.25;对于层流,C=16,n=1,即布拉修斯公式。
气液混合物密度的计算公式为ρm=αρg+(1-β)ρl,混合速度定义为 Um=Usg+Usl。不同均相模型的差异主要体现在等效粘度μm的定义,McAdams模型[1]等效粘度为 μ-1m=xμ-1g+(1 - x)μ-1l,Cicchitti模型[2]等效粘度为 μm=xμg+(1 - x)μl,Dukler I模型[3]等效粘度为 μm= ρm[xμg/ρg+(1 - x)μl/ρl]。均相模型对泡状流、弹状流预测结果偏低,而对于环状流或弹环过渡流预测结果偏高。
3.3.3 Friedel关系式
Friedel模型[4]是目前唯一考虑了重力和表面张力等因素对两相流动摩擦压降影响的均相流经验模型:
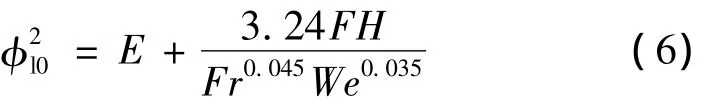

该模型与中国科学院Zhao等[5]在2001年报道的利用俄罗斯IL-76失重飞机实验数据吻合度较好。
3.3.4 Muller-Steinhagen 关系式
Muller-Steinhagen模型[6]给出的均相流摩擦压力梯度计算公式为:

式中:C=A+2(B-A)x,A、B分别为液体和气体的单相压力梯度:
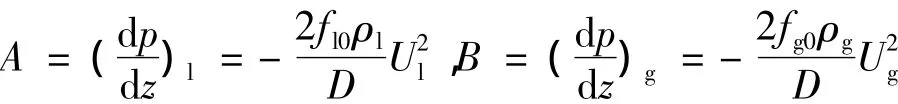
单相流体连续摩擦因子f0的计算公式由Churchill[7]给出。
令人遗憾的是在众多气液两相流摩擦压降模型中,目前还没有一个关系式能准确描述所有工况。流动参数不同时,不同模型给出的气液两相流能量损失机理不同,含气率和压降计算方法也不同。因此实际应用中需要根据具体工况合理选择不同的计算关系式。
4 垂直管路上升气液两相流压降特性
循环预冷系统垂直管路上升气液两相流达到稳定状态时基本满足如下3条假设:
(1)管路气液两相流内部无剧烈相变,处于准热力学平衡状态;
(2)气相、液相介质均不可压缩,密度变化很小,可视为常数;
(3)相对于液体质量流量,推进剂蒸发量及注入气体质量为小量,受低温推进剂阻碍作用而迅速减速,在较大范围内管路截面含气率和体积含气率近似相等,气液两相速度偏差量为小量。
基于上述假设,可以采用均相模型分析循环预冷系统垂直管路上升气液两相流压降特性,同时结合部分分相流方法进行比对验证。
4.1 压降影响因素对比分析
结合低温动力系统循环预冷垂直上升流动管路典型结构参数,对影响管路压降的各因素及多个摩擦压降关系式进行比对分析,所有工况管路出口压力为105Pa。
图1给出了不同管路内径(D)、不同管长(L)、不同总质量流量(G)和不同干度(x)的6种工况,分别采用 McAdams、Cicchitti、Dukler I、Friedel和 Muller-Steinhagen(图中用“Muller”表示)5个关系式计算得 到的垂直管路上升液氧-氧气两相流压降。

图1 液氧-氧气两相流6种工况垂直管路压降计算值Fig.1 LOX-O2 two phase flow pressure drop calculated results for six different flow conditions
对比工况1与工况6可知,摩擦压降和重力压降随着管长的增加而增大,重力压降增加幅度更为明显,而加速压降量级很小,虽然略有增加,但对总压降贡献不大。结合工况2,气液两相流干度对系统压降影响特性为干度越大,含气率越高,两相流密度越小,重力压降随之降低,而速度会有所增加,最终导致摩擦压降增大;由于摩擦压降所占比例较小,其增加值未能抵消重力压降降低引起的变化,总压降下降。从工况1与工况4的压降计算情况可以看出,当管路内径增大时,摩擦压降和加速压降会明显降低,总压降几乎全部为重力压降贡献。这主要是因为当质量流量恒定时,随着管径的增加,流速下降,依据达西公式,摩擦压降与管径的平方成反比、与速度的平方成正比,摩擦压降会迅速降低;而加速压降与管径的平方成反比,也会随管径的增大快速减小。工况3管长最大,干度最低,达到了总质量流量G=0.5 kg/s的5个工况的最大总压降,主要因素包括两个方面:大长径比和低干度使得重力压降非常大,管长的优势弥补了因为干度降低而导致的摩擦压降下降。最终使得重力压降显著增加而摩擦压降基本不变,从而增大了总压降。
工况5给出了增大质量流量后压降计算值,与工况3对比可以发现,两者干度、管长相等导致重力压降相等,而摩擦压降显著增加,甚至接近重力压降的60%¯70%(不同摩擦压降模型计算结果有所差异),总压降随质量流量的增大而明显增加。这主要是因为当管径恒定、质量流量增加时,流速增大,摩擦压降与与流速的平方成正比,随之迅速增大,成为总压降中不可忽略的一部分。
图2给出了6种工况不同计算关系式得到的重力压降与总压降的比值。对于所有计算工况,重力压降在总压降中所占比例基本都接近或高于60%,工况4接近100%,表明重力压降是垂直管路上升气液两相流总压降最重要的组成部分,其数值大小直接决定着总压降。摩擦压降随两相流干度或质量流量增加而增大,可以一定程度地降低重力压降所占比例,但不会取代重力压降成为主导因素。加速压降是总压降中比例最低的因素,对于大部分工况其比例不足10%。工况1与工况6中重力压降所占比例基本相等,表明管长的增加可以同时增大重力压降和摩擦压降,但是对两者的比例关系影响很小;而管路长径比的减小可以显著降低摩擦压降,提高重力压降比例,如工况4。
对于5个经验或半经验摩擦压降计算关系式,Friedel关系式在计算中给出的摩擦压降数值最高,McAdams、Cicchitti、Dukler I和 Muller-Steinhagen 关系式给出的数值接近,这主要是因为只有Friedel关系式考察了表面张力对摩擦压降的贡献。
4.2 压降值实验验证
图3对比了压降值计算结果与4次管路实验数据,实验工况为管路内径D=0.108 m,管长L=1 m,总质量流量 G=0.9 kg/s,干度 x=8.8 ×10-3。从图3可以看出,在该工况下,管路长径比很小(9.26),明显低于4.1节的6个计算工况(100¯320),质量流量相近,计算结果表明摩擦压降、加速压降均与重力压降存在数量级的差异,总压降体现为重力压降,其计算值与实验数据吻合程度较好,5种计算关系式得到的数据基本一致,较好地验证了4.1节压降特性分析部分结论。表1给出了总压降计算值、4次实验压降值及误差分析。
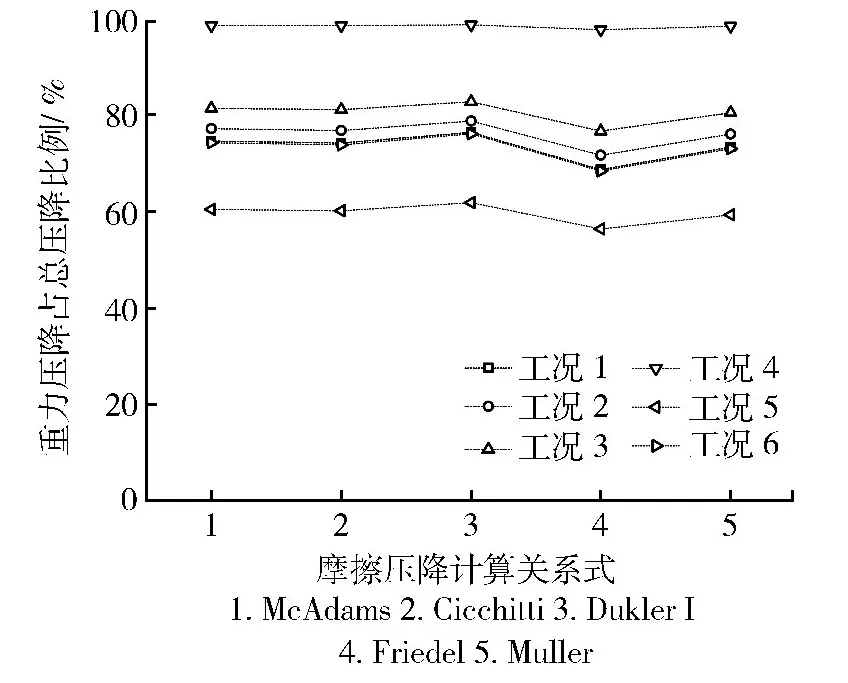
图2 液氧-氧气两相流6种工况垂直管路总压降中重力压降比例Fig.2 LOX-O2 two phase flow gravity pressure drop proportions for six different flow conditions
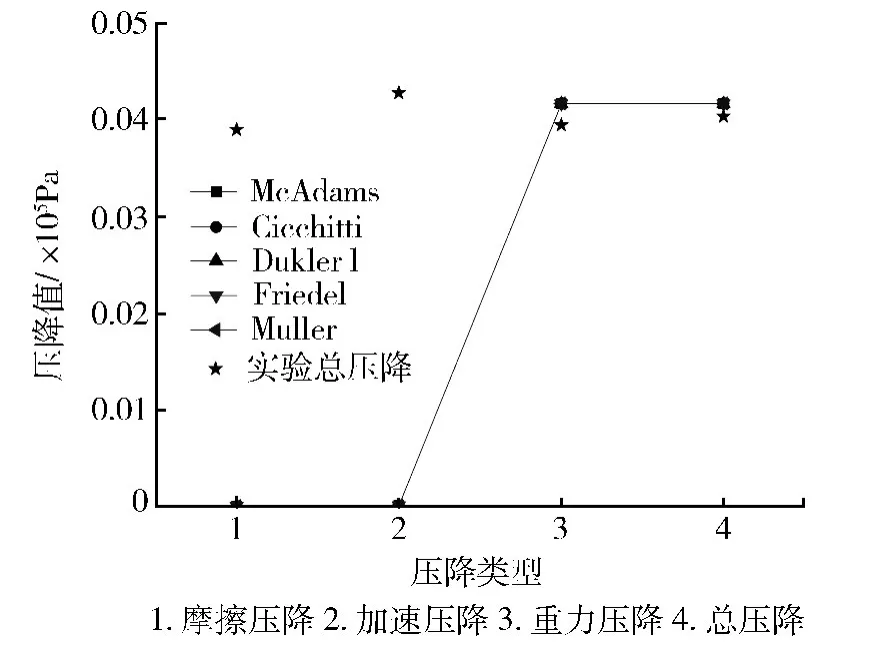
图3 液氧-氧气两相流压降计算值与实验数据对比图Fig.3 LOX-O2 two phase flow pressure drop calculated results versus experimental data

表1 总压降计算值、4次实验压降值及误差分析Table 1 Total pressure drop calculated result,experimental data and error analysis
5 循环预冷系统引射气等效关系
5.1 不同气体间压降等效关系
不同气体间压降等效关系推导的要求为在满足引射气工作压力、低温动力系统循环预冷质量流量和垂直管路上升流动压降相等的前提下,获得不同引射气之间的体积流量关系,从而实现两者的模拟替代。
根据上文的分析,加速压降在总压降中所占比例很低,可以忽略。根据总压降相等、液体流量相等,并引入质量流量G与体积流量Q的关系可以得到:
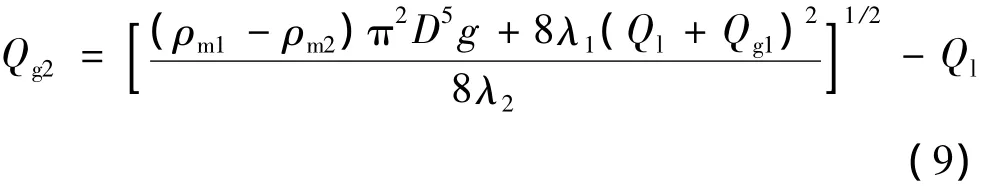

按照上文循环预冷系统垂直管路上升气液两相流3条假设和压降因素分析,管路可以近似采用均相模型分析,重力压降是总压降中最为重要的因素。λ为沿程阻力系数,对重力压降无影响;影响不同气体间压降等效的最核心参数为气液两相流密度,它对重力压降和摩擦压降都具有决定性作用,而其关键因素为截面含气率α。由于不同气体密度与液体密度相比均为小量,对两相流密度贡献不大,垂直管路上升气液两相流压降相等的等效条件近似为两者截面含气率相等,进一步转化为不同引射气体的体积流量近似相等,即:

式中:ψ为修正系数,需要根据不同工况进行具体分析,对于小长径比管路,ψ约为1。
5.2 等效关系实验验证
图4给出了氦气引射液氧缩比实验系统的原理示意图,流量测量装置设置在泵前阀上端的推进剂输送管上。结合氦气引射液氧缩比实验管路模型,用氧气等效氦气,以循环预冷质量流量为对比数据,对上述等效关系式进行验证。验证工况为垂直管路上升流动出口压力105Pa,管路内径0.03 m,管长4 m,氦气质量流量 0.003 kg/s,温度 288 K,引射压力 1 MPa,等效关系式修正系数取ψ=1,转化后得到氧气质量流量为0.024 2 kg/s。
表2给出了计算模型及实验得到的稳定状态的循环预冷质量流量。从相对误差分析中可知,转化后的计算结果与四次实验均值相对误差为2.120%,转化关系式在该工况下验证效果较好。对于其它工况,需要对修正系数ψ进行有针对性的分析。

图4 引射循环预冷实验系统示意图Fig.4 Schematic of gas injection circulation precooling experiment system
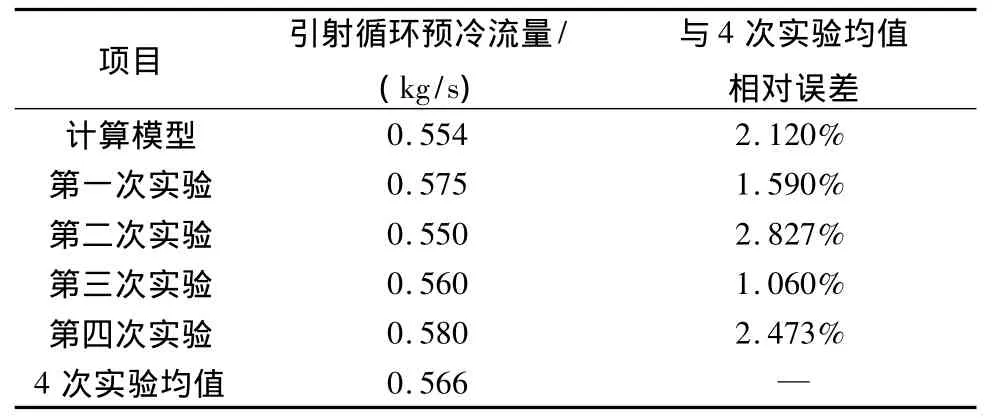
表2 循环预冷质量流量计算值、实验值及误差分析Table 2 Mass flow rate calculated result,experimental data and error analysis
6 结论
对管路气液两相流压降计算关系式进行了梳理,运用部分关系式,基于均相和分相模型对垂直管路上升低温液氧-氧气两相流压降组成及影响因素进行了系统分析和实验验证,并结合循环预冷系统背景,将分析结果应用于工程实践。主要结论如下:
(1)重力压降是垂直管路上升气液两相流总压降最重要组成部分,随着管长或密度的增加而增大,其数值大小直接决定着总压降;
(2)摩擦压降随管长、速度或密度增加而增大,可以一定程度地降低重力压降所占比例,但不会取代重力压降而成为主导因素;管路长径比的增大会显著增加摩擦压降数值;
(3)加速压降是总压降中比例最低的因素,对于大部分工况其比例不足10%,在一般工程分析中可以忽略;
(4)垂直管路上升气液两相流影响压降的最核心参数为两相流密度,由于液体与气体之间的巨大密度差,密度的决定性因素为截面含气率;
(5)基于压降分析结论,可以初步实现工程中低温动力系统引射循环预冷引射气的等效转化;对于长径比较小的管路,气体间的等效关系近似为G2=G1ρ2/ρ1;对于某些特殊工况,需要具体分析修正系数ψ的取值。
1 McAdams W H,Woods W K,Bryan R L.Vaporization inside horizontal tubes-II-Benzene-oil mixtures[J].Trans.ASME,1942,64:193-199.
2 Cicchitti A,Lombardi C,Silvestri M,et al.Two-phase cooling experiments:pressure drop,heat transfer and burnout measurements[J].Energia Nucleare,1960,7:407-425.
3 Dukler A E,Wicks M,Cleveland R G.Pressure drop and hold-up in two-phase flow,Part B:An approach through similarity analysis[J].AIChE Journal,1964,10:38-51.
4 Friedel L.Improved friction pressure drop correlations for horizontal and vertical two-phase pipe flow[C].European Two-Phase Group Meeting.Italy,Ispra:E2,1979.
5 Zhao JF,Lin H,Xie JC,et al.Experimental study on pressure drop of two-phase gas-liquid flow at microgravity conditions[J].Journal of Basic Science and Engineering,2001,9(4):373-380.
6 Muller-Steinhagen H,Heck K.A simple friction pressure drop correlation for two-phase flow in pipes[J].Chemical Engineering Processing,1986,20:297-308.
7 Churchill S W.Friction-factor equation spans all fluid flow regimes[J].Chemical Engineering 1977(11):91-92.

