气动斯特林制冷机关键参数的模拟与实验

蔡 诗 李 娜 陈 曦 蒋珍华 夏宇栋 吴亦农

(1上海理工大学能源与动力工程学院 上海 200093)

(2中国科学院上海技术物理研究所 上海 200083)

1 引言

分置式斯特林制冷机可以有效地削弱压缩机振动对冷头安装和使用的影响。相比牛津型，气动斯特林的膨胀机不使用电机辅助驱动排出器，可以使整机质量和体积减小，并有效降低能耗。目前，气动斯特林制冷机以其特有的优势被应用于军事、国防、空间探测、商业等领域。从事气动斯特林制冷机研发的单位主要有以色列 RICOR［1-2］、法国 Thales［3-4］、美国Sunpower［5-6］和德国AIM公司等。气动斯特林制冷机虽然结构简单，但也正因为其驱动力为排出器两端压差所构成的气动力，排出器的相位只能被动调节;同时，排出器受力直接影响排出器的运动，而排出器的运动直接决定了制冷机的性能。因而非常有必要对气动斯特林制冷机相关参数进行全面的研究。

本文对一台无背压腔的气动斯特林制冷机进行理论研究，并与实验结果比对，阐述了阻尼、刚度对于制冷机的制冷量、排出器运动以及膨胀机性能的影响规律。

2 气动斯特林制冷机的经典动力学分析

以一台无背压腔式气动斯特林制冷机为例，进行动力学分析，排出器受力如图1所示。

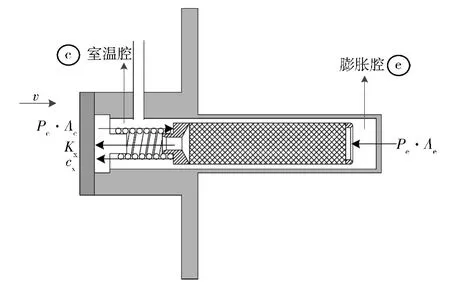
图1 膨胀机受力分析图Fig.1 Schematic diagram of forces for expander

式中:m为排出器质量，kg;c为阻尼，(N˙s)/m;K为弹簧刚度，N/m;Ac和Ae分别为排出器室温腔侧和膨胀腔侧截面积，m2;P为压力，Pa;Fgas为气动力，N;x为位移，m;˙x为速度，m/s;¨x为加速度，m/s2。

由于压缩机产生的压力波经过蓄冷器后有一定的滞后，所以令膨胀腔的压力波滞后室温腔压力波的相位为θ。室温腔压力波:Pc=P0+Pcmsin(ωt+θ)，膨胀腔压力波:Pe=P0+Pemsinωt。故:

若忽略压力波流经蓄冷器后改变的相位θ，考虑排出器两端截面积差，由式(1)—(3)可得:

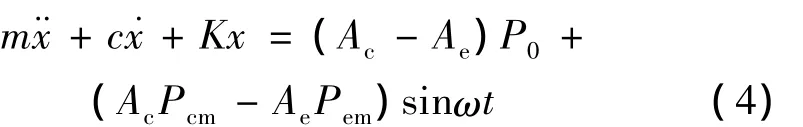
求解该二阶常系数非其次线性微分方程的特解即可得到排出器位移表达式。

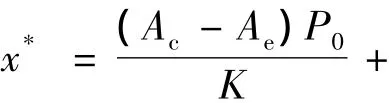
由式(5)可知，排出器位移与作用于其两端的截面大小有关。相同条件下，Ac越大，排出器的位移波幅值越大。相同Ac下，Ae增大，排出器的位移波幅值越小。

常数项表示，由于截面积差的存在，使排出器位移波幅值有一定量的偏置。对于本制冷机而言，当Ac－Ae＞0时，排出器向冷端偏置，即正偏置，则膨胀腔体积减小。若正偏置量较小，由于膨胀腔存在一定空体积，制冷机性能会随正偏置的存在变好;若正偏置量较大，则膨胀腔的体积过小，相当于排出器有用行程减小，制冷机性能会随正偏置的存在变差。

若忽略排出器两端截面的面积差，则:

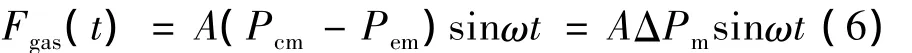
式中:ω为角频率，rad/s;t为时间，s;Pcm和Pem分别为室温腔侧和膨胀腔侧的压力波幅值;ΔPm为流经蓄冷器前后压力波的压差幅值，反映了压力波经过蓄冷器后衰减的大小，与蓄冷器的阻力特性相关。因而，蓄冷器的阻力特性直接影响排出器所受气动力的大小，从而影响制冷机的性能。

由式(1)、(2)、(6)可得:

排出器的往复运动为持续简谐激励下的强迫振动。简谐激励下系统的响应由初始条件引起的自由振动、伴随强迫振动发生的自由振动和等幅稳态强迫振动3部分组成。由于存在阻尼，自由振动属于衰减的瞬态振动;而稳态强迫振动即稳态响应，是与激励同频率、共同存在的简谐振动［7］。所以求解该二阶常系数非其次线性微分方程的特解即可得到排出器位移表达式。

式中:xm为位移波幅值，φ为排出器位移波领先压力波的相位。由该表达式可知，位移幅值与截面积、压差幅值成正比;刚度越大，阻尼越大，排出器位移幅值越小;动子质量也影响排出器位移幅值。

根据式(1)、(2)可以得到惯性项m¨x较小或较大时排出器受力的矢量图，如图2所示。

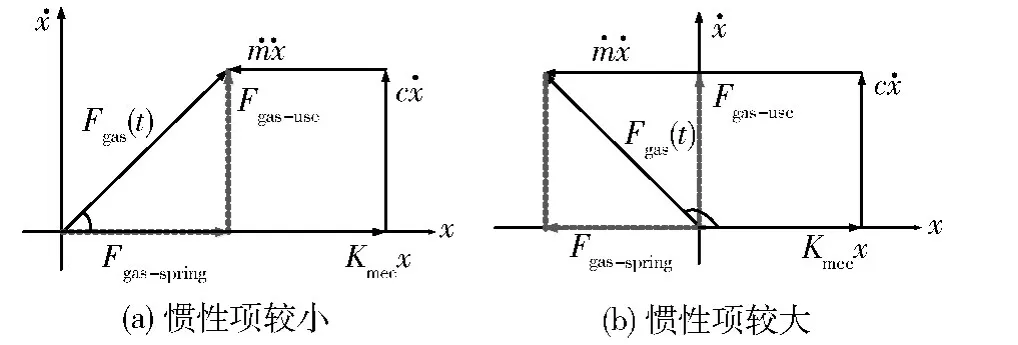
图2 排出器受力矢量图Fig.2 Vector force diagram of displacer

排出器所受的气动力一部分抵消了阻尼力，即

Fgsa－use=c˙x;另一部分相当于气体弹簧Fgas-spring=－Kgasx。当惯性项较小时，气体弹簧削弱了机械弹簧的刚度，如图2a;当惯性项较大时，气体弹簧加强了机械弹簧的刚度，如图2b。故等效弹簧刚度［8-9］为:

式中:Kmec、Kgas分别为机械弹簧刚度、气体弹簧刚度，N/m。

对于回热式制冷机［10］有:

理论制冷量:

式中:τ为排出器往复运动的周期，s;f为频率，Hz。

综上所述，压力波、排出器作用面积、刚度与阻尼直接影响气动斯特林制冷机的性能，本文主要研究弹簧刚度、膨胀机阻尼对制冷机性能的影响。

3 阻尼的影响

若仅对阻尼进行估算，则压缩机阻尼系数取ξc=0.09，膨胀机阻尼系数取 ξe=0.1¯0.2［11］。阻尼系数可通过衰减法进行实验测量。

式中:cc为临界阻尼，(N˙s)/m;ξ为阻尼系数;D为阻尼，(N˙s)/m。

阻尼在制冷机中起到能量耗散的作用，它将一部分气动力所做的功以热的形式耗散，因此阻尼增大必然会减少制冷量的产生，从而降低制冷机的性能。阻尼大小与气体热物理性质、机械装配和结构设计等相关［12］。通过Q-test试验可测得斯特林制冷机在真空下的阻尼，即机械阻尼。本文对一台2 W@80 K气动斯特林制冷机进行实验研究，通过式(13)和式(14)，可估算该款制冷机的膨胀机阻尼 De=1.8(N˙s)/m。

压缩机阻尼仅对制冷机功耗有影响，而膨胀机阻尼主要影响制冷机产生的冷量，对制冷机功耗有较小的影响。如图3所示，当增大压缩机输入功时，制冷量增大。由于受到蓄冷器换热能力的限制，冷指的COP并不是单调递增，而是不断增长到某一程度后缓慢趋向于某一值或下降呈抛物线。在模拟中，考虑了丝网的换热损失、轴向导热损失以及穿梭损失，模拟所得的COP曲线与实验结果吻合度很高。

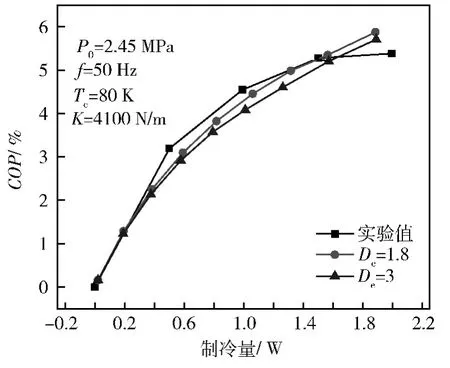
图3 不同膨胀机阻尼下，膨胀机COP随制冷量的变化Fig.3 COP of expander versus cooling power at different damping of expander

阻尼还包括间隙密封的气体阻尼等。当膨胀机在制冷后，氦气粘度的变化导致排出器的气体阻尼变化［13］;当膨胀机的行程变大，膨胀腔内的阻尼也会变大，而并不是一个定值。在模拟中，将膨胀机的阻尼视为定值，忽略了阻尼变化对制冷机性能产生的影响。从图3中可以看到，膨胀机阻尼取 De=1.8(N˙s)/m和De=3(N˙s)/m时，膨胀机COP相差5%以内。

如图4，膨胀机阻尼增大，制冷量减小，压缩机PV功减小。如图5所示，阻尼越大，位移相位越小(即排出器位移波领先压缩活塞位移波的相位)，膨胀机的COP越低。

4 刚度的影响

除了充气压力、运行频率，刚度是气动斯特林制冷机的又一可调参数。刚度直接影响了排出器的位移相位，从而影响了制冷机的性能。因此，确定制冷机某一工况下的最优刚度是很有必要的。本文所研究的气动斯特林制冷机采用柱弹簧，而柱弹簧的安装长度直接决定了刚度的大小。

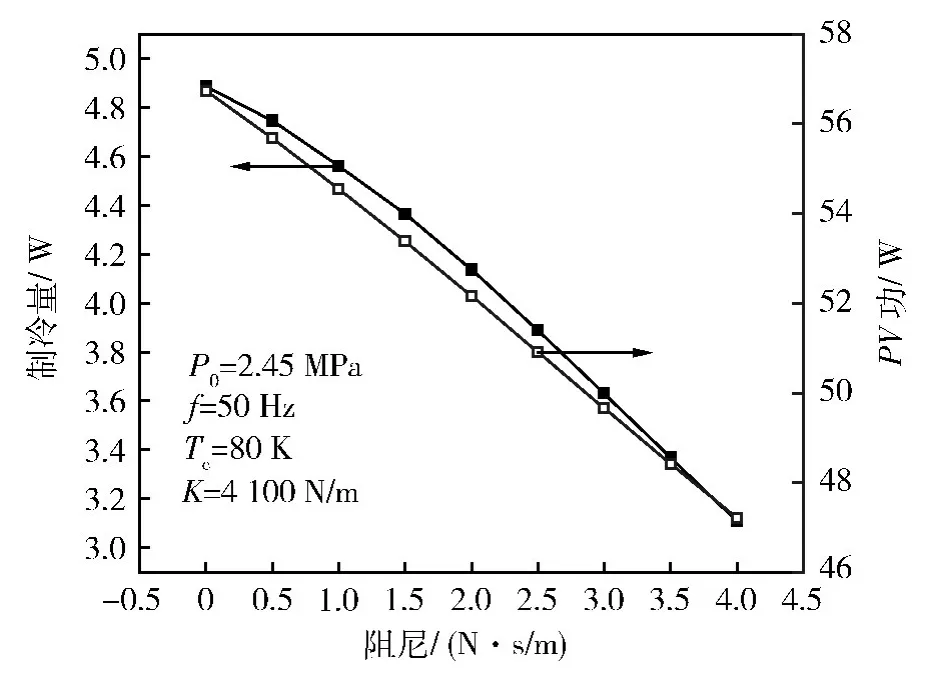
图4 制冷量与压缩机PV功随膨胀机阻尼的变化Fig.4 Cooling power and PV power of compressor versus damping of expander

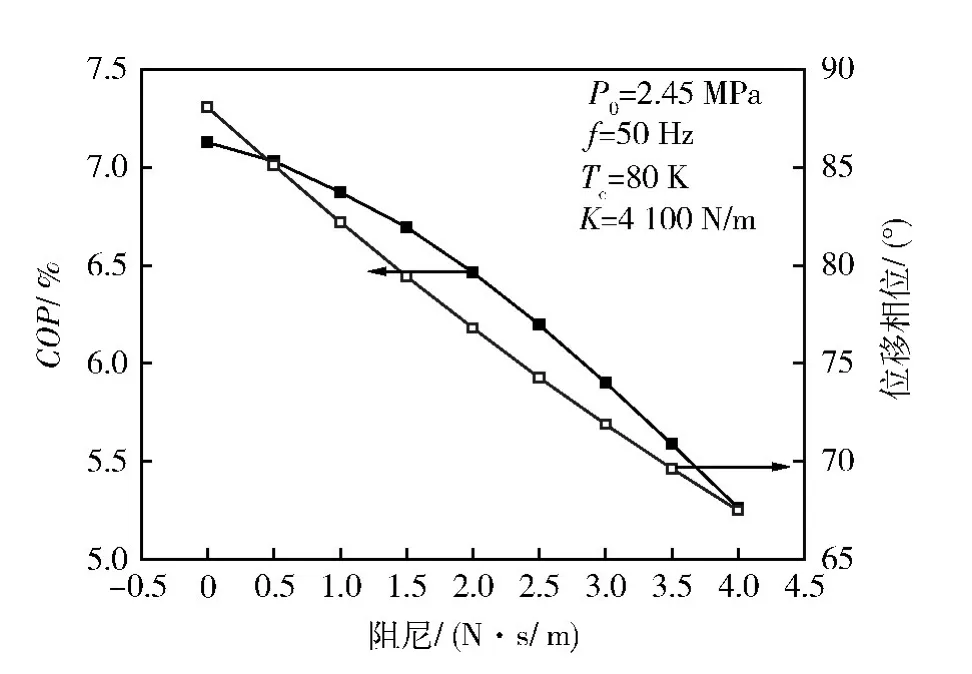
图5 膨胀机COP与位移相位随膨胀机阻尼的变化Fig.5 COP of expander and phase angle for displacement versus damping of expander

从图6中可以看到，在K为4 465和4 705 N/m时，模拟结果与实验结果的吻合度较高，模拟与实验的误差在±5%以内。

如图7所示，弹簧刚度越大，位移相位越大。若弹簧刚度降低则膨胀机冷端位移波与压力波的相角增大，即降低了冷端质量流与压力波的相角。对于斯特林制冷机而言，当冷端的质量流滞后压力波30°时，其制冷效率最高［14-16］，所以调节弹簧刚度可以调节冷端相角，使其更接近最优的相角。研究结果表明，在某一冷量下，存在最优弹簧刚度，使位移相位最优，从而使膨胀机的COP最高。模拟所得的最优刚度比实验值小，是因为模拟情况下的制冷机为理想工况，忽略了一部分损失，从而使得膨胀机所需的气动力较实际小，因而最优的刚度也较实际的小。

图6 不同刚度下，制冷量随膨胀机COP的变化Fig.6 COP of expander versus cooling power at different stiffness of expander

图7 膨胀机COP及位移相位随刚度的变化曲线Fig.7 COP of expander and phase angle of displacement versus stiffness of expander

5 结论

基于经典动力学，对一台无背压腔气动斯特林制冷机进行了理论研究和实验研究，在忽略压力波经过蓄冷器的相位变化的情况下，得到排出器位移的表达式。通过建模，得到了制冷机的一系列性能参数，将模拟结果与实验数据进行比对，阐述了误差因素。通过数值建模，得到了阻尼、刚度对制冷机性能的影响。研究结果表明:

(1)膨胀机阻尼越大，位移相位越小;制冷量越小，压缩机出口PV功越小，冷指COP下降。

(2)膨胀机弹簧刚度越大，位移相位越大，存在最优刚度，使排出器位移相位最优，从而获得最优COP值。

1 Veprik A M，Riabzev S V，Vilenchik G S，et al.Ultra-low vibration split Stirling linear cryogenic cooler with a dynamically counterbalanced pneumatically driven expander［J］.Cryogenics.2005，45:117-122.

2 Alexander Veprik，Arnon Meromi，Avraharn Leshecz.Novel technique of vibration control for split Stirling cryocooler with linear compressor［C］.SPIE.3061:640-650.

3 MulliéJ C，Bruins P C，Benshop T，et al.Development of the LSF95× ×2nd generation flexure bearing coolers［R］.International Cryocooler Conference 12，2004.

4 Benshop T，MulliéJ C，Helmonds H.6W full flexure Stirling cooler for cryosystem program［R］.ESA Cryogenics Workshop，2003.

5 Kim S，Unger R，Wiseman R.New Sunpower CryoTel DT［J］ Cryocooler，ICE2012.

6 Kim S，Holliday E，Unger R，et al.The development of CryoTel DT［J］.Cryocooler，ICC17.

7 李娜.小型分置式斯特林制冷机气动性能研究［D］.上海:中国科学院上海技术物理研究所，2008.Li Na.Study on pneumatic characteristic of miniature pneumatically driven split-Stirling cryocooler［D］.Shanghai:Shanghai Institute of Technical Physics，Chinese Academy of Sciences，2008.

8 A T A M de Waele，WLiang.Basic dynamics of split Stirling refrigerators［J］.Cryogenics，2008，48:417-425.

9 Veprik A M，Riabzev S V，Vilenchik G S，et al.Ultra-low vibration split Stirling linear cryogenic cooler with a dynamically counterbalanced pneumatically driven expander［J］.Cryogenics，2005，45:117–122.

10 陈国邦，汤珂.小型低温制冷机［M］.北京:科学出版社，2009.

11 刘心广，刘冬毓，王永，等.斯特林制冷机排出器气动力特性研究［J］.低温工程，2007(5):10-14.Liu Xinguang，Liu Dongyu，Wang Yong，et al.A study on gas dynamic characteristic of displacer in Stirling cryocooler［J］.Cryogenics，2007(5):10-14.

12 熊超，杨开响，李娜，等.线性压缩机与气动斯特林冷指效率匹配研究［J］.工程热物理学报，2014，35(2):228-232.Xiong Chao，Yang Kaixiang，Li Na，et al.Studying on matching efficiency between linear compressor and pneumatic Stirling cooler［J］.Journal of Engineering Thermophysics，2014，35(2):228-232.

13 Park S J，Hong Y J，Kim H B，et al.An experimental study on the phase shift between piston and displacer in the Stirling cryocooler［J］.Current Applied Physics，2003:449-455.

14 Ray Radebaugh.Development of the pulse tube refrigerator as an efficient and reliable cryocooler［R］.Proceeding of Institute of Refrigeration，London，2000:1-27.

15 Ray Radebaugh，Lewis M，Luo E C，et al.Inertance tube optimization for pulse tube refrigerators［J］.Advances in Cryogenic Engineering，AIP，Melville，NY，2006，51:59-67.

16 Swift Greg.Thermoacoustics:A unifying perspective for some engines and refrigerators［M］.New York:Acoustical Society of America，2002:103-104.