基于GPU 的并行粒子群神经网络设计与实现

陈 风，田雨波，杨 敏

（江苏科技大学 电子信息学院，江苏 镇江212003）

0 引 言

人工神经网络 （artificial neural networks，ANN），简称神经网络 （neural networks，NN），正在各个领域得到越来越广泛的应用。粒子群优化 （particle swarm optimization，PSO）作为一种容易实现、收敛速度快的全局优化算法［1］，正在逐渐代替常用的误差反向传播 （back propagation，BP）算法应用到NN 的训练中［2］。面对计算复杂度较高的问题时，运算时间长是粒子群神经网络 （PSO－NN）的一大问题，并行化加速是解决该问题的有效思路。

除了NN 存储结构和样本训练的并行性［3－5］，PSO－NN还存在PSO 算法天然具备的群体中个体行为的并行性。相比用计 算 机 群［6，7］、多 核CPU［8］或FPGA 等 专 业 并 行 设备［9］加速PSO 算 法，利 用 图 形 处 理 器 （graphic processing unit，GPU）并行加速PSO 算法［10－13］具备硬件成本低的最显著优势。特别是2007年NVIDA 公司推出了统一计算设备架构 （compute unified device architecture，CUDA），不需要借助复杂的图形学知识，良好的可编程性使其迅速成为当前最为流行的GPU 编程语言。

本文在GPU－PSO 的研究基础上，设计并实现了一种基于CUDA 的并行PSO－NN 求解方法，并对一简单测试函数逼近进行了实验测试。本文创新之处在于，从GPU－PSO解决的问题看，将GPU－PSO 用来加速训练NN；从PSONN 的实现方式上，用GPU 并行加速训练PSO－NN。实验结果表明，该方法能加速NN 的训练，减少NN 的训练时间，相对于基于CPU 的串行PSO－NN，基于GPU 的并行PSO－NN 在保证训练误差的前提下取得了超过500 倍的计算加速比。

1 基于CUDA 的并行PSO－NN 算法

1.1 标准PSO－NN算法

PSO 算法是Kennedy和Eberhart于1995 年提出的一种基于群体智能的优化算法，其简单易实现，具备较强的全局搜索和收敛能力，用于优化NN 权阈值能比BP－NN 获得更好的收敛精度和更强的预测能力［2］。PSO－NN 的核心思想在于粒子与NN 之间的4 个对应：粒子维数对应NN权阈值的数目，粒子位置对应NN 的权阈值，粒子速度对应NN 权阈值的变化，粒子适应度值对应NN 的输出误差。

本文使用的PSO 算法版本为带惯性权重、全局拓扑结构的PSO 算法。粒子群由N 个粒子组成，每个粒子的位置代表优化问题在D 维搜索空间 （D 为NN 权阈值的数目）中的一个潜在的解。PSO－NN 中，采用粒子各维与NN 各权阈值一一对应的原则，将每个粒子被编码成一个向量，比如将图1 （图中已将权值和阈值合并表示为权阈值）所示的一个输入层2 节点、隐层3 节点、输出层1 节点的NN编码成一个13维的粒子

式中：i——粒子数，i＝1，2，...，N。特别要指出的是，这里未采用矩阵编码策略，而采用向量编码策略，主要是考虑到1.3节中方便将粒子位置、速度等信息存储在线性的GPU 全局内存中。

算法的速度更新和位置更新公式如下

其中，i＝1，2，...，N，d＝1，2，...，D；c1和c2是学习因子，非负的常数；r1和r2是介于 ［0，1］的均匀分布的随机数；Vid（t）∈ ［－Vmax，Vmax］，Vmax限制了粒子飞行的最大速度，Xid（t）∈ ［－Xmax，Xmax］，Xmax限定了粒子搜索空间的范围，可设定Vmax＝kXmax，0≤k≤1；w 是惯性权重，介于 ［0，1］，用来平衡粒子的全局探索能力和局部开发能力。

标准PSO－NN 算法的流程如下：

（1）读入训练样本和测试样本，数据预处理，设定最大迭代次数Tmax。

图1 2－3－1结构的神经网络模型

（2）随机初始化每个粒子的位置Vid（t）和速度Xid（t）。

（3）初始化个体最优位置Pbestid（t）和全局最优位置Gbestd（t）。

（4）更新每个粒子的速度Vid（t）和位置Xid（t）。

（5）计算每个粒子对应的适应度值 （即NN 的输出误差）F（Xi）。

（6）更新个体最优位置Pbestid（t）和全局最优位置Gbestd（t）。

（7）若达到最大迭代次数Tmax，则执行步骤 （8），否则返回步骤 （4）。

（8）将训练样本和测试样本带入训练好的NN，得到网络输出。

1.2 CUDA编程架构

CUDA 采用CPU 和GPU 异构协作的编程模式，CPU负责串行计算任务和控制GPU 计算，GPU 以单指令多线程 （single instruction multiple threads，SIMT）执行方式负责并行计算任务。内核函数 （kernel）执行GPU 上的并行计算任务，是整个程序中的一个可以被并行执行的步骤。CUDA 将线程组织成块网格 （grid）、线程块 （block）、线程 （thread）这3个不同的层次，并采用多层次的存储器结构：只对单个线程可见的本地存储器，对块内线程可见的共享存储器，对所有线程可见的全局存储器等。kernel函数中，Grid内的Block之间不可通信，能以任意顺序串行或并行地独立执行；Block内的Thread之间可以通信，能通过存储共享和栅栏同步有效协作执行。CUDA 程序流程通常包括以下6个步骤：①分配CPU 内存并初始化；②分配GPU 内存；③CPU 到GPU 数据传递；④GPU 并行计算；⑤计算结果从GPU 传回CPU；⑥处理传回到CPU的数据。

1.3 基于CUDA的并行PSO－NN算法设计

常见的NN 神经元节点和训练样本数目往往只有十几或几十个，利用NN 存储结构或样本训练的并行性比较适合计算机集群等并行计算方式［3－5］，对于GPU 来说其算法并行程度还是不够，因为GPU 线程数为十几或几十时难以充分发挥其强大的并行计算能力。对于较复杂的问题，PSO－NN 中的粒子数往往可以达到上百个乃至更多，利用群体中粒子行为的并行性可以比较充分发挥GPU 的并行计算能力。

2009年，Veronese和Krohling 首次应用CUDA 实现了 对PSO 算 法 的 加 速［10］，掀 起 了GPU 加 速PSO 算 法 的 研究热潮，近几年GPU－PSO 的研究趋势集中在以下2 个方面：①有GPU 架构特色的各种PSO 算法变种；②GPUPSO 解决实际问题。国内文献对GPU 加速PSO 算法的研究相对较少。张庆科等在文献 ［12］中概述了CUDA 架构下包括PSO 算法在内的5种典型现代优化算法的并行实现过程，在并行PSO 算法部分给出了文献 ［14］中的实验结果。蔡勇等近期在文献 ［13］中给出了并行PSO 算法较详细的设计过程和优化思路，取得了90倍的加速比。

本文所述的基于CUDA 的并行PSO－NN 算法属于上文所述GPU－PSO 研究趋势的第2个方面，解决的实际问题是NN 的加速训练。PSO－NN 算法非常适合CUDA 架构的原因有2点：一是可并行部分 （NN 的训练）的执行时间占整个程序执行时间的绝大部分；二是CPU 和GPU 之间无需频繁通信，数据传输的时间开销只占整个程序执行时间的极小部分。

为简单起见，本文使用前述标准PSO－NN 算法，采用粒子与线程一一对应的并行策略，利用PSO算法固有的三大并行性：速度更新和位置更新的并行性，计算粒子适应度的并行性，更新Pbest适应度值和位置的并行性，以及CUDA 架构特有的并行性：更新Gbest时的并行规约 （reduction）算法，将GPU－PSO－NN的算法流程设计如图2所示。

图2 基于CUDA 架构的并行PSO－NN 算法流程

GPU－PSO－NN 算法的步骤如下：

（1）CPU 端读入训练样本和测试样本，数据预处理。

（2）CPU 端调用malloc （）函数和cudaMalloc （）函数，分别在CPU 端和GPU 端分配变量空间。

（3）CPU 端初始化粒子的位置、速度等信息。

（4）CPU 端调用cudaMemcpy （）函数，将CPU 端粒子信息传至GPU 全局内存；CPU 端调用cudaMemcpyTo－Symbol（）函数，将CPU 端训练样本传至GPU 常量内存。

（5）CPU 端调用kernel函数，执行GPU 上的并行计算任务，完成NN 的训练。

（6）CPU 端调用cudaMemcpy （）函数，将GPU 端有用信息传回至CPU 端。

（7）CPU 端将训练样本和测试样本带入训练好的NN，查看结果。

（8）CPU 端 调 用free （）函 数 和cudaFree （）函 数，释放CPU 端和GPU 端已分配的变量空间。

以上步骤中，完成加速训练NN 的步骤 （5）是GPUPSO－NN 算法的核心，其伪代码如下：

以上伪代码中的kernel 4 需要找出适应度值最小的粒子编号，这对单线程算法来说非常简单的任务，在大规模并行架构上实现时却会变成一个复杂的问题。当粒子数大于块内最大线程数1024 （计算能力2.0 及以上）或512（计算能力2.0 以下）时，在CUDA 架构上需用2 次并行Reduction实现，程序具体实现时分为2个kernel。第1个kernel启动等于粒子数的线程数，找到各个线程块中的最小值；第2个kernel启动等于第1个kernel中线程块数的线程数，找到这些最小值的最小值，即当前全局最优值。当前全局最优值再与旧的全局最优值对比，决定是否需要更新。不能只使用1个kernel的原因在于：CUDA 架构能通过调用＿＿syncthreads（）使线程块内的线程同步，但不能使所有线程同步，所有线程的同步只能通过kernel的结束来保证。当粒子数小于等于块内最大线程数1024 或512时，在kernel函数中启动等于粒子数的线程数做1次并行Reduction即可。

2 GPU－PSO－NN算法性能优化

2.1 粒子 （线程）数目和线程块大小的设计

一个线程束 （Warp）包含索引相邻的32个线程，流多处理器 （stream multiprocessor，SM）以Warp为单位调度和执行线程，因此将粒子数目和线程块大小都设计成32的倍数值。具体实现时，每个线程块中的线程数目在kernel 1、kernel 2、kernel 3中尽量取128、192、256这样的典型值，在kernel 4中为了充分利用共享内存第1个Reduction时尽量取大 （计算能力2.0 及以上的块内最大线程数为1024，计算能力2.0以下的块内最大线程数为512），第2个Reduction时取第一个Reduction的线程块数。

2.2 最小化线程分支

SIMT 执 行 模 式 会 导 致 线 程 分 支 （thread divergence）特别耗时，应尽量减少Warp内的分支数目。以kernel 4中的并行规约为例 （实验中至少有32个线程，这里简单起见只列出8个线程），图3的方案具有明显的线程分支，在第一次求min中，只有那些索引为偶数的线程才执行求min，相邻线程行为不同。图4的方案分支就较少，表现在相邻线程行为相同，都求min或者都不求min。

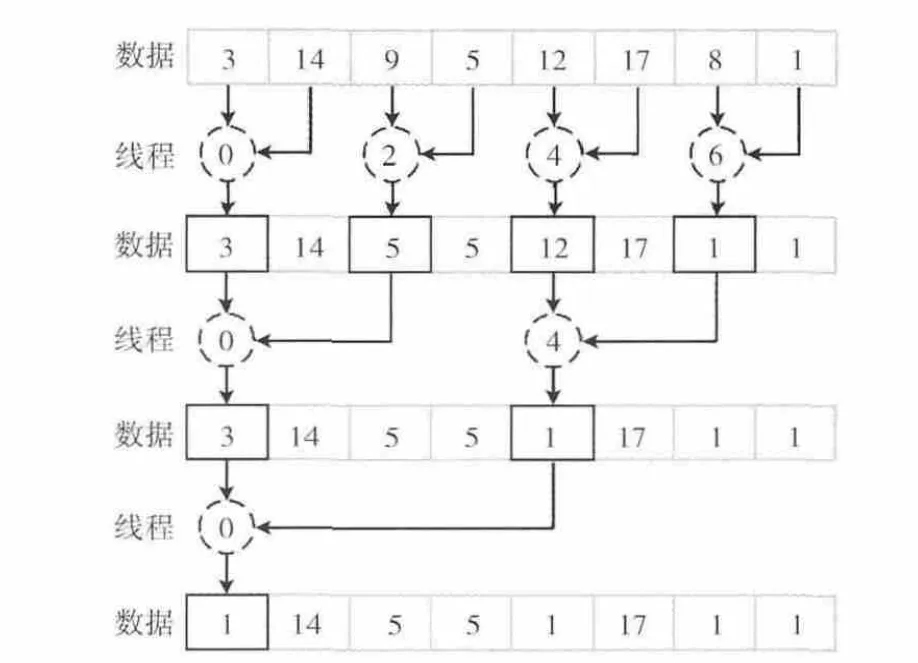
图3 大量线程分支的并行规约求极值方案

图4 最小化线程分支的并行规约求极值方案

2.3 合并访问全局存储器

粒子位置、速度等信息在CPU 内存中以二维形式存储，如图5所示 （图中d＝D－1，n＝N－1），而GPU 全局内存是一维形式，将粒子位置、速度等信息在GPU 全局内存中布局涉及到合并访问 （coalesced access）的问题。简单地说，相邻的线程访问相邻的数据，即可满足合并访问的要求。合并访问能使传输数据时的速度接近全局存储器带宽的峰值。粒子位置信息在GPU 全局内存中按粒子顺序存储 （文献 ［13，15］等就是采用的这种方式），如图6所示，虽然简单直观但不符合合并访问的要求，会造成访存效率大幅下降。这里采用文献 ［16］所述的存储布局方法，如图7所示，访存时同时访问各个粒子的同一维，满足合并访问的条件，提高了访存效率。粒子速度信息的存储布局与粒子位置信息类似。

图5 粒子位置信息在CPU 内存中的存储

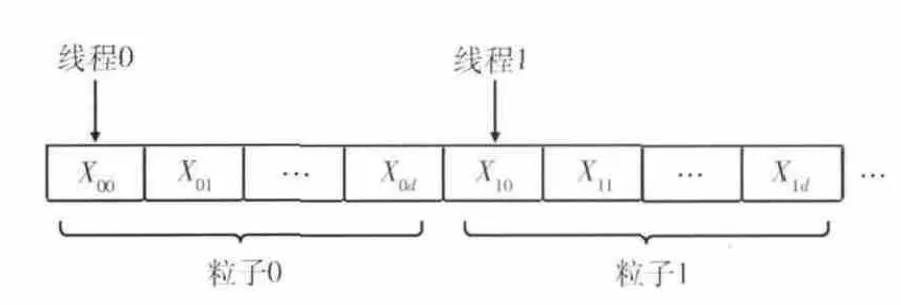
图6 粒子位置信息在GPU 全局内存中的存储（没有合并访问）

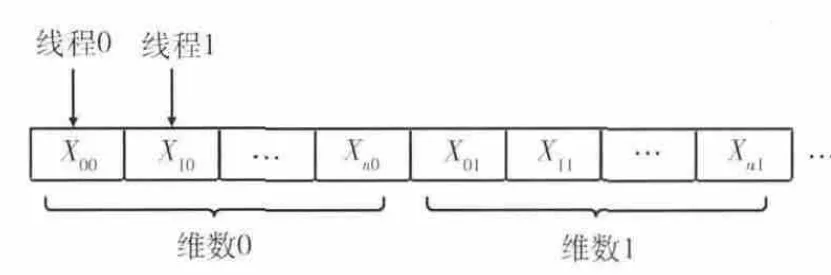
图7 粒子位置信息在GPU 全局内存中的存储 （合并访问）

2.4 最大化使用共享存储器

每个SM 提供最多48KB 的共享存储器，比全局存储器的访问速度快得多，但只对块内线程可见。应尽量使用共享存储器来保存全局存储器中在kernel函数的执行阶段需要频繁使用的那部分数据。以kernel 4中的并行Reduction为例，每次规约时将先将全局内存中的数据保存至共享内存，规约时反复使用共享内存上的数据，规约完成后再将共享内存上的结果保存至全局内存。

2.5 最大化使用常量存储器

GPU 上共有64KB对所有线程可见的常量存储器，以数据 “不可变”作为代价换取比全局存储器更快的访问速度。PSO－NN 用于训练的样本数据量较多 （十几、几十乃至上百个数据），都是常量且重复利用。因此和粒子速度、位置等信息存储在全局内存中不同，将训练样本数据存放在常量内存中，加快访存速度。

2.6 最小化CPU 和GPU 之间的数据传输

GPU 上执行PSO 的粒子速度更新需要大量的随机数。早期的GPU 上没有自带的随机数生成库，需要将CPU 产生的随机数传至GPU （传输时间降低计算性能）［14］，或编写GPU 随机数生成函数 （使用不方便）［17］。目前，可以使用CURAND 库中的curand＿uniform （）函数在GPU 上产生随机数，这样使整个迭代过程都在GPU 上完成，避免在CPU 和GPU 之间频繁传输数据带来的时间损耗。

3 实验结果与分析

本文采用一个简单测试函数逼近对GPU－PSO－NN 算法和CPU－PSO－NN 算法进行加速性能测试。

该函数表达式如式 （4）所示，在定义域 ［－4，4］内有两个峰值点，如图8所示。训练函数集和测试函数集分别有101和100组输入，如式（5）和式（6）所示，带入式（4）可得其理论输出。NN训练样本的输出均方误差（MSE），即粒子的适应度值，反映NN对测试函数的逼近程度。

图8 测试函数

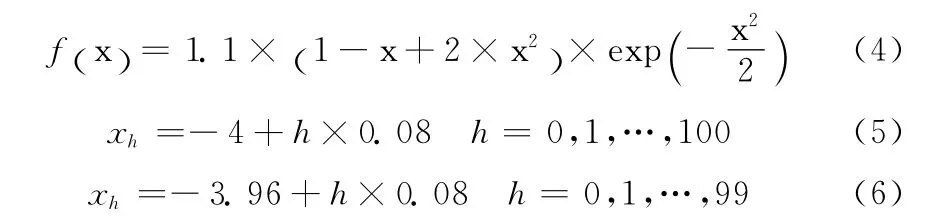
仿真计算过程中，NN 结构设定为1－10－1，即输入层1节点、隐层10节点、输出层1节点，权阈值数目为31（粒子维数），如图9所示。隐层激活函数为双极性S型函数，其表达式如式 （7）所示。输出层激活函数为线性函数，其表达式如式 （8）所示

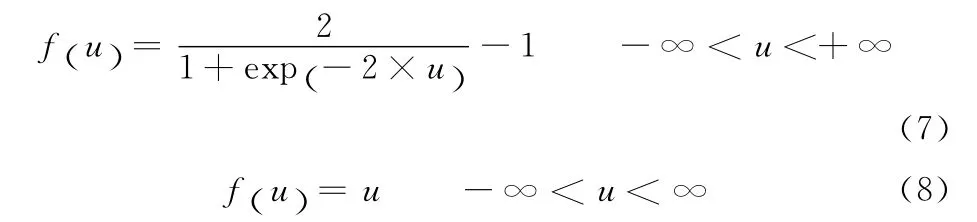
惯性权重w 取值0.9 至0.4线性递减。学习因子c1和c2均取2.05。k取值0.5。训练次数Tmax取值1000。实验所采用的计算平台见表1。为保证结果的可靠性，实验数据为20次实验去掉最大值和最小值之后18次的平均值。

“加速比”Siteration是最常用的加速性能指标，定义为PSO－NN 算法在相同的粒子数和相同的迭代次数 （1000）下CPU 程 序 运 行 时 间Tcpu－iteration和GPU 程 序 运 行 时 间Tgpu－iteration的比值

图9 实验所用的1－10－1结构的神经网络模型

表1 计算平台

实验结果见表2。

表2 PSO－NN 作简单测试函数逼近取得的加速比

对表2中的数据做如下分析：

（1）PSO－NN 完成1000 次迭代的运行时间，在CPU程序中随着粒子数的翻倍大致呈翻倍趋势；在GPU 程序中当粒子数小于等于16384 时呈小幅增长趋势，大于等于32768时呈大幅增长趋势 （其原因见 （2））。

（2）该GPU 共13个SM，每个SM 的最大驻留线程数为2048，总最大驻留线程数为26624。当粒子数 （线程数）小于等于16384时，各个粒子执行时间相似，但同步 （包括kernel函数结束对应的所有线程的同步，以及＿＿syncthreads（）调用对应的线程块内线程的同步）所消耗的时间随着粒子数的增多而小幅增长，造成PSO－NN 的运行时间呈小幅增长趋势；当粒子数大于等于32768 时，线程总数已超过26624，PSO－NN 的运行时间呈大幅增长趋势（当粒子数翻倍，运行时间增加不到1倍是基于以下3个原因的共同作用：①粒子数翻倍对应运行时间翻倍；②粒子数增多对应同步时间增加；③线程切换能掩盖存储器访问延迟，显著减少执行时间）。

分析表2中的数据可得如下结论：

（3）粒子数越多，获得的加速比越高，PSO－NN 最高获得了566倍的加速比。随着粒子数的翻倍，当粒子数小于等于16384，加速比大致翻倍；当粒子数大于等于32768，加速比仍能增加但增速放缓。

（4）GPU－PSO－NN 具 有 与CPU－PSO－NN 同 样 的 寻 优稳定性。随着粒子数的不断增多，CPU 程序和GPU 程序的训练误差 （即NN 的MSE）不断减小；粒子数相同时，CPU 程序和GPU 程序的训练误差大致相同或相近。

（5）大幅增加粒子数是适应GPU 计算架构的特殊方法。若GPU 端使用比CPU 端多的多的粒子，则可以在运行时间增加极为有限的情况下大幅降低训练误差。

另外作如下推断：

（6）使用相同实验设备，笔者曾在CUDA 架构下对Sphere、Rosenbrock、Rastrigrin、Griewangk 这4个基准测试函数进行了数值测试，以比较GPU－PSO 算法相对CPUPSO 算法的加速性能，结果表明，当粒子数目小于100时，往往不能得到加速。文献 ［13］也进行了类似测试，使用的粒子数目最小也为400 （具体为400、1200、2000、2800、5000）。而本文的实验当粒子数目为32和64时，也得到了加速。PSO－NN 算法本质上就是适应度函数为NN输出误差的PSO 算法，问题维数很多 （1－10－1简单结构的NN 就已有31维）且计算时反复使用，比起一般的基准测试函数计算复杂度高的多。

可以推断，用GPU 作并行加速时，PSO－NN 由于适应度函数计算量大，比起一般的PSO 能获得更好的加速比，更适应CUDA 并行计算架构。

（7）对于该测试函数的NN 逼近问题，当NN 训练样本的MSE小于0.001起，测试样本输出曲线与实际曲线基本拟合，肉眼尚能明显分清差别；当MSE 小于0.0002起，测试样本输出曲线与实际曲线基本重合，肉眼不易分清差别；当MSE小于0.0001起，测试样本输出曲线与实际曲线几乎完全重合，肉眼几乎不能分清差别。

根据经验，一般而言CPU 端粒子数应多于问题维数，以保证种群的多样性，但粒子数过多又会增加计算时间，降低寻优效率，显著恶化CPU 端PSO－NN 算法性能而造成加速比虚假现象。当粒子数为128、256、512、1024 时，其CPU 程序对应的MSE大致在0.001至0.0001之间，不妨认为这些CPU 程序是 “高效的CPU 程序” （粒子数过少则逼近精度较差，“不合格”；粒子数过多则浪费计算时间，“不值得”），其对应的GPU 程序取得了5.6至44.0的加速比。

注意到本实验的测试函数逼近问题所用NN只有1个输入层节点、1个输出层节点，网络结构非常简单，问题维数较少（31维），实际问题往往是多输入、多输出、更多的隐层节点数、更多的权阈值数目，带来的直接好处是，“高效的CPU 程序”对应的粒子数以及获得的加速比也会相应增加。

可以推断，NN 解决的问题越复杂，获得的加速比越高。

4 结束语

本文采用CUDA 架构设计并实现了PSO－NN 的并行加速求解。通过粒子与线程一一对应的并行策略，采用适应GPU 计算的优化设计方法，实现了对NN 训练这一占整个程序绝大部分执行时间的可并行部分的加速计算，并对一简单测试函数逼近进行了数值仿真实验。实验结果表明，相对于传统的基于CPU 的串行PSO－NN，基于GPU 的并行PSO－NN 在寻优稳定性一致的前提下取得了超过500倍的计算加速比。本文提出的基于GPU 的并行PSO－NN 设计方案和优化思路可以推广应用到其它类似实际问题的分析和设计中。

［1］Poli R，Kennedy J，Blackwell T.Particle swarm optimization：An overview ［J］.Swarm Intelligence，2007，1 （1）：33－57.

［2］TIAN Yubo，LI Zhengqiang，WANG Jianhua.Model resonant frequency of rectangular microstrip antenna based on particle swarm neural network ［J］.Journal of Microwaves，2009，25 （5）：45－50 （in Chinese）.［田雨波，李正强，王建华.矩形微带天线谐振频率的粒子群神经网络建模 ［J］.微波学报，2009，25 （5）：45－50.］

［3］Ganeshamoorthy K，Ranasinghe D N.On the performance of parallel neural network implementations on distributed memory architectures ［C］／／8th IEEE International Symposium on Cluster Computing and the Grid，2008：90－97.

［4］GUO Wensheng，LI Guohe.On designing artificial neural networks on parallel computer cluster［J］.Computer Applications and Software，2010，27 （5）：12－14 （in Chinese）.［郭文生，李国和.人工神经网络在并行计算机集群上的设计研究 ［J］.计算机应用与软件，2010，27 （5）：12－14.］

［5］ZHANG Daiyuan.Training algorithm for neural networks based on distributed parallel calculation ［J］.Systems Engineering and Electronics，2010，32 （2）：386－391 （in Chinese）.［张代远.基于分布式并行计算的神经网络算法 ［J］.系统工程与电子技术，2010，32 （2）：386－391.］

［6］Singhal G，Jain A，Patnaik A.Parallelization of particle swarm optimization using message passing interfaces（MPIs）［C］／／IEEE World Congress on Nature ＆Biologically Inspired Computing，2009：67－71.

［7］Deep K，Sharma S，Pant M.Modified parallel particle swarm optimization for global optimization using message passing interface ［C］／／IEEE Fifth International Conference on Bio－Inspired Computing：Theories and Applications，2010：1451－1458.

［8］Wang D Z，Wu C H.Parallel multi－population particle swarm optimization algorithm for the uncapacitated facility location problem using OpenMP ［C］／／IEEE Congress on Evolutionary Computation，2008：1214－1218.

［9］Maeda Y，Matsushita N.Simultaneous perturbation particle swarm optimization using FPGA ［C］／／IEEE International Joint Conference on Neural Networks，2007：2695－2700.

［10］Veronese L，Krohling R.Swarm’s flight：Accelerating the particles using C－CUDA ［C］／／Proceedings of the IEEE Congress on Evolutionary Computation，2009：3264－3270.

［11］Calazan R M，Nedjah N，de Macedo Mourelle L.Parallel GPU－based implementation of high dimension particle swarm optimizations［C］／／IEEE Fourth Latin American Symposium on Circuits and Systems，2013：1－4.

［12］ZHANG Qingke，YANG Bo，WANG Lin，et al.Research on parallel modern optimization algorithms using GPU ［J］.Computer Science，2012，39 （4）：304－311 （in Chinese）.［张庆科，杨波，王琳，等.基于GPU 的现代并行优化算法［J］.计算机科学，2012，39 （4）：304－311.］

［13］CAI Yong，LI Guangyao，WANG Hu.Research and implementation of parallel particle swarm optimization based on CUDA ［J］.Application Research of Computers，2013，30 （8）：2415－2418 （in Chinese）. ［蔡勇，李光耀，王琥.基于CUDA 的并行粒子群优化算法的设计与实现 ［J］.计算机应用研究，2013，30 （8）：2415－2418.］

［14］Zhou Y，Tan Y.GPU－based parallel particle swarm optimization ［C］／／Proceedings of the IEEE Congress on Evolutionary Computation，2009：1493－1500.

［15］Mussi L，Daolio F，Cagnoni S.Evaluation of parallel particle swarm optimization algorithms within the CUDA architecture［J］.Information Sciences，2010，181 （20）：4642－4657.

［16］Roberge V，Tarbouchi M.Efficient parallel Particle Swarm Optimizers on GPU for real－time harmonic minimization in multilevel inverters ［C］／／38th Annual Conference on IEEE Industrial Electronics Society，2012：2275－2282.

［17］Bastos－Filho CJA，Oliveira MAC，Nascimento DNO，et al.Impact of the random number generator quality on particle swarm optimization algorithm running on graphic processor units［C］／／IEEE 10th International Conference on Hybrid Intelligent Systems，2010：85－90.