基于混合蛙跳的量子遗传算法

董玉民，赵 莉

（1.青岛理工大学 网络中心，山东 青岛266033；2.青岛市海慈医疗集团，山东 青岛266033）

0 引 言

量子遗传算法将传统的遗传算法引入量子空间，在遗传算法的优势上进一步提高算法性能。量子遗传算法由Narayanan等人提出［1］，并引起了社会各界学者的广泛关注。虽然量子编码固有的叠加性使算法的收敛能力大幅提高，但出现早熟的可能仍然是其一个不可忽视的问题。为进一步提高量子遗传算法的性能，对算法的改进研究一直在进行。

为提高算法的寻优能力，在基本的量子遗传算法的基础上，引入混合蛙跳算法，结合模拟退火准则及动态的参数调整，提出一种基于混合蛙跳的改进算法。将改进后的新算法与其它对比算法，分别用于测试函数的优化，从实验的结果中可以看出，新的改进算法有效提高了算法的求解能力，在符合问题精度要求的基础上搜索出函数的满意解。

1 基于量子的遗传算法

量子遗传算法将量子计算融合到传统的遗传算法，抛弃遗传算法中复杂的操作算子，仅使用旋转门策略更新种群。采用量子位编码染色体，使得量子遗传算法获得更丰富的个体，利于全局问题的求解［2］。

1.1 量子计算

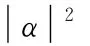
1.2 算法实现

这样的编码方式，可以用一个基因位同时表示任意多不同状态，充分体现种群的多样性。

种群中个体的更新，使用量子旋转门来完成。量子旋转门实际上就是改变了量子位的叠加态，相当于变异操作。

1.3 算法流程

基本的量子遗传算法的主要执行步骤可以描述如下：

步骤1 初始化算法中的各项参数并进行种群Q（t）的初始化。

步骤2 对初始种群的所有个体进行坍塌测量，得到状态值P（t）。

步骤3 对P（t）进行适应度函数评价，记录种群中最优个体。

步骤4 当未达到种群的最大迭代次数，循环执行下述操作：

（1）增加种群的进化代数。

（2）对种群Q（t－1）进行坍塌测量，记录状态P（t）。

（3）对P（t）中的所有进行适应度函数评价，记录个体的适应度值。

（4）用量子旋转门更新个体。

（5）将全局最优保存在P（t）中，并记录个体信息。

2 基于量子的遗传算法改进

随着量子遗传算法的发展，出现了大量对算法的优化改进。文献 ［3－8］中，研究者分别就染色体的编码、种群构造、旋转门等方面，提出了对量子遗传算法的各种改进，在一定程度上优化了算法。本文针对算法容易出现过早收敛，无法快速收敛的缺陷，在基本量子遗传算法中引入混合蛙跳，进一步改进算法的不足。

2.1 改进策略

2.1.1 分组寻优

混合蛙跳算法由Eusuff和Lansey 在2003 年提出［9］，建立在模因算法与粒子群算法的基础上，并结合了二者的优点。混合蛙跳算法的核心特征，是协调并利用局部信息和全局信息。算法将种群分为不同的组，各组同时进行组内的3次跳跃搜索，当完成组内寻优之后，重新混合，进行新一轮的分组寻优。

利用混合蛙跳的分组寻优，可以减少算法的迭代次数，加快算法的收敛。经典的混合蛙跳算法，个体移动步长的大小直接影响算法的优化结果，若步长太大，个体很可能越过最优解并逐渐远离，若步长太小，个体有可能陷入局部极值。考虑将惯性调节参数引入，使个体的移动步长随着组内搜索同步调节。

改进后的个体第一次跳跃（局部最优更新）的更新公式

改进后的个体第二次跳跃 （全局最优更新）的更新公式

2.1.2 模拟退火准则

模拟退火算法［10］，利用了物理中固体物质的退火原理，温度逐渐由高到低的同时，在解空间中搜索问题的全局最优。

采用模拟退火算法中的这一概率性接收准则，以最小值问题为例：

2.1.3 动态旋转门量子遗传算法中通常采用固定的旋转门，在新算法中使用动态调整旋转角的方式。动态自适应旋转角调节，可以在算法的寻优过程中灵活控制，将旋转角度由初始时的较大值逐渐减小到后期的较小值，使个体的搜索范围由大变小。

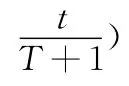
2.2 基于混合蛙跳的量子遗传算法

在基本的量子遗传算法中，引入混合蛙跳的分组策略，提出一种新的改进量子遗传算法，简记为QSFLG，借鉴分组寻优的方式将群体分组，并进行组内的三次跳跃更新，在完成分组寻优后重新混合，使用动态的量子旋转门更新个体，并使用模拟退火准则概率性接收新解，之后再利用量子非门进行群体的量子变异。

QSFLG 的基本流程描述如下：

（1）算法的初始化阶段

步骤1 初始化算法参数，包括最大迭代次数MAXGEN，种群规模SIZEPOP，种群分组数目GROUPNUM，每个分组中个体数目GROUPIND，组内最大迭代次数GROUPMAXGEN，初始温度T0，冷却系数α，冷却系数Pi。

步骤2 量子位编码染色体，种群初始化。

步骤3 对种群中的每一个个体进行坍塌操作，记录状态值。

步骤4 对状态值进行适应度函数评价，记录最优个体的适应度值。

（2）分组寻优阶段

步骤5 将种群中所有个体按适应度值升序排列，排序后第一个个体分配到1号子种群，第二个个体分配到2号子种群，……，第GROUPNUM 个个体分配到GROUPNUM 号子种群，第 （GROUPNUM＋1）个个体分配到1号子种群……直到种群中所有个体分配完。

步骤6 进行子种群的组内寻优。分别对各组内的个体进行3次跳跃，当组内最差个体的第1次跳跃结果没有优化，则进行第2 次跳跃，当第2 次跳跃的结果没有优化，则进行第13次跳跃，随机生成个体。

步骤7 当组内寻优达到最大迭代次数，则进行步骤8，否则跳转到步骤4。

（3）整体寻优阶段

步骤8 利用模拟退火准则概率性接收新解。

步骤9 使用动态的量子旋转门，更新群体中的个体。再次利用模拟退火准则进行判断，以概率接收劣质解。

步骤10 使用量子非门，对种群中的个体进行量子变异操作。

步骤11 若达到算法的最大迭代次数，则输出最优解，算法结束，否则继续执行步骤4。

3 函数优化

3.1 测试函数

为测试算法的性能，使用以下5个最小值测试函数进行仿真实验。

（1）f1（x）＝x6－15x4＋27x2＋250 x∈ ［－100，100］。

函数f1（x）有3个局部极小值，理论全局最小值为7。

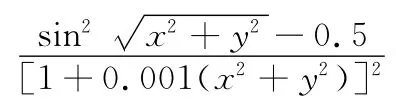
此函数为Shaffer函数的变形，由最大值问题变形为求最小值，变形后的理论最小值为－1。

f3（x，y）有6个局部极值，理论最小值为－1.031628。

Sphere函数是一个简单的单峰函数，常被用于测试算法的性能，理论最小值为0。

Griewank函数是标准的多模态函数，具有很多局部极值，理论最小值为0。

3.2 实验设计

将提出的基于混合蛙跳的量子遗传算法 （QSFLG）、量子遗传算法 （QGA）、混合蛙跳算法 （SFLA）和粒子群优化算法 （PSO）分别作用于5 个测试函数，进行实验的对比。

测试函数Sphere和Griewank取变量的维数为5。QSFLG 和QGA 采用量子位编码的方式，编码长度为20；QSFLG 的变异概率为0.01，初始温度为100，冷却系数为0.99。算法其它参数的设置见表1。

3.3 实验结果与分析

3.3.1 实验一

对于5个测试函数，每个算法分别进行50 次独立实验。算法的求解精度为10－3时，即算法的最优解与测试函数的理论最优值之差小于10－3时，记为算法求解成功。定义算法的函数优化成功率：求解成功的次数与独立运行的总数之比。

算法的仿真函数测试实验，在MATLAB R2008 环境下进行，4种算法的实验结果详见表2。

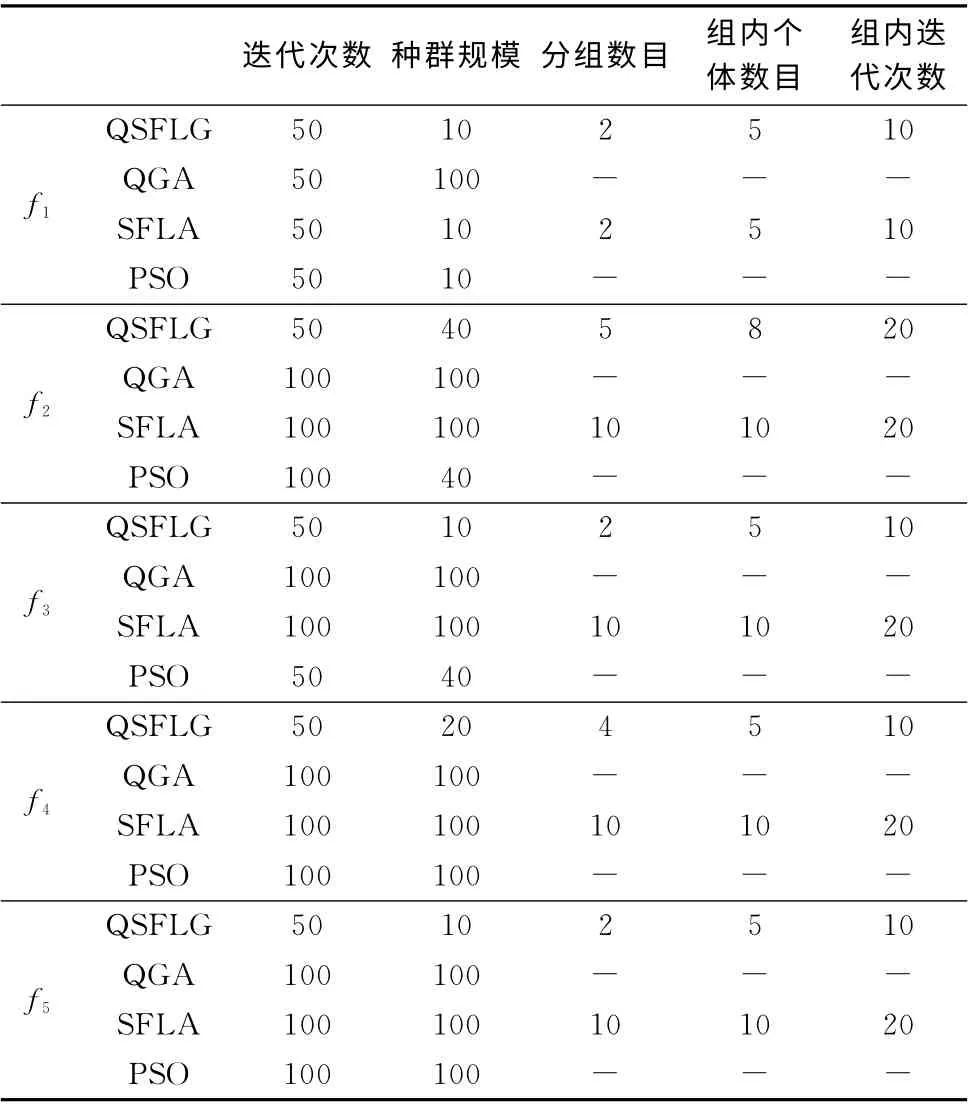
表1 测试函数的参数设置

表2 测试函数的实验结果

从表2的实验结果中可以看出，改进的基于混合蛙跳的量子遗传算法对5个测试函数的优化能力较好。与其它3个算法相比，QSFLG 使用较小的种群规模和迭代次数，但求解出的函数最优值比另外3 个函数更接近理论最优值。进行50次独立实验，QSFLG 的求解成功率最高，每次求解都能找到满足精度要求的全局最优解。但QSFLG 仍然存在不足，表现为算法的运行时间略长。虽然QSFLG 的运行时间比PSO 长，但略微牺牲时间代价来换取更为准确的全局最优解，是可以接受的。

算法的收敛能力是另一个评价算法性能优劣的关键。图1～图5分别给出了4种算法求解函数最优解的进化收敛曲线图。

图1 测试函数f1 的收敛曲线

图2 测试函数f2 的收敛曲线

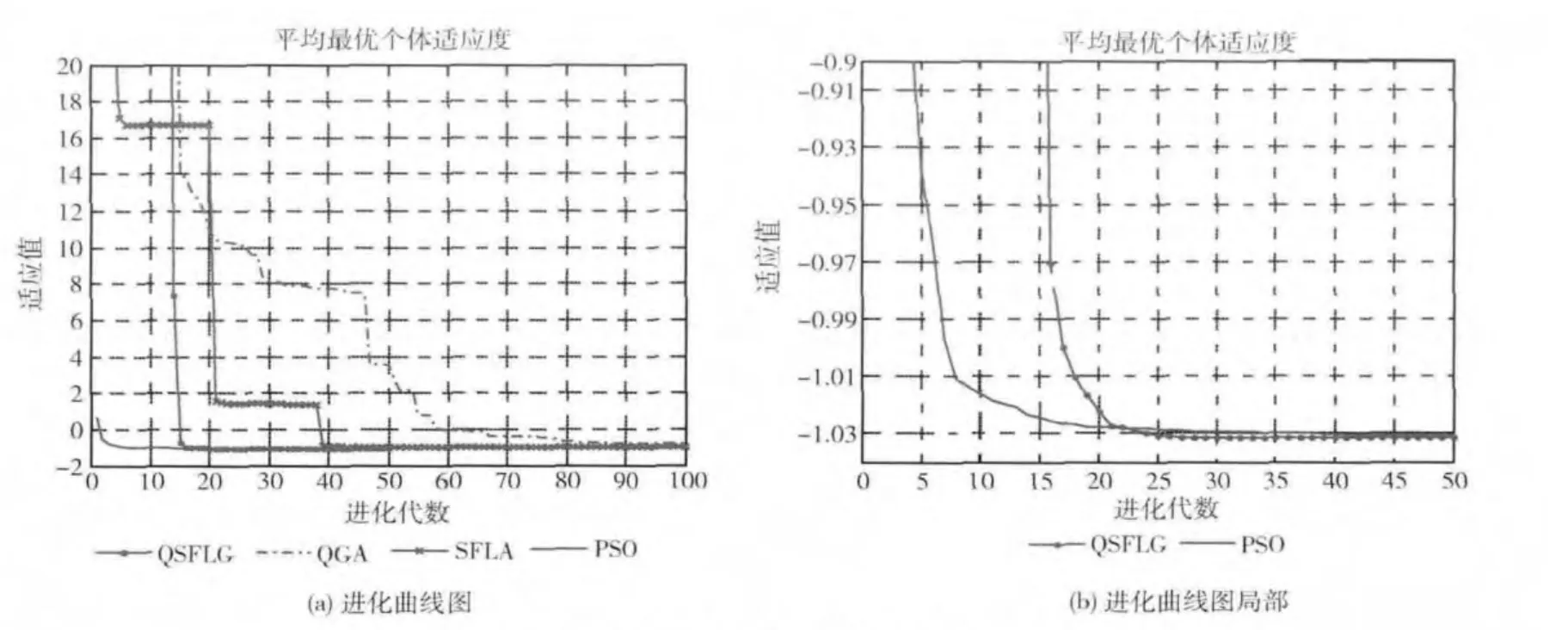
图3 测试函数f3 的收敛曲线

图4 测试函数Sphere的收敛曲线

图5 测试函数Griewank的收敛曲线

从函数的优化曲线图中可以看出QSFLG 对测试函数的求解表现出更好的收敛性能。虽然QSFLG 在求解前4个函数时，初始阶段的收敛速度较为缓慢，不是4种算法中最好的，但随着优化的进行，QSFLG 的表现逐渐优于其它3种算法，稳定收敛。综合看来，改进的基于混合蛙跳的量子遗传算法QSFLG 能以较小的种群规模以及较小的迭代次数，快速且稳定的收敛到一个很接近问题理论最值的满意解。

3.3.2 实验二

在实验二中，提高算法的求解精度为10－6，每个算法独立运行50次。表3中给出了4种算法对测试函数优化的结果。

表3 算法的成功次数

从实验结果看来，改进的基于混合蛙跳的量子遗传算法QSFLG 有效提高了量子遗传算法的性能。当问题的求解精度定义较高时，QSFLG 相对于其它3种算法，仍然具有较高的求解成功率。实验结果说明，改进的新算法能更好的求解出满足用户需要的全局最优解，提高了量子遗传算法的整体性能。

4 结束语

针对量子遗传算法存在的不足，在传统的量子遗传算法的基础上，提出一种新的改进算法。算法引入混合蛙跳的分组寻优策略并优化更新公式，同时考虑动态调整量子旋转门和量子变异，再用模拟退火的概率接收准则判断是否接收产生的新解。将提出的新算法用于函数优化，利用测试函数的优化结果来评价算法的性能。实验结果表明，改进的基于混合蛙跳的量子遗传算法有效避免了算法的早熟收敛，能搜索到满足问题精度的全局最优，提高了算法求解能力。

［1］LIANG Changyong，BAI Hua.Advances in quantum genetic algorithm ［J］.Application Research of Computers，2012，29 （7）：2401－2405（in Chinese）.［梁昌勇，柏桦.量子遗传算法研究进展［J］.计算机应用研究，2012，29 （7）：2401－2405.］

［2］HUANG Liming，XU Ying，YU Ruiqin.Improved quantum genetic algorithm and its application ［J］.Computer Enginee－ring and Design，2009，30 （8）：1987－1990 （in Chinese）.［黄力明，徐莹，于瑞琴.改进的量子遗传算法及应用 ［J］.计算机工程与设计，2009，30 （8）：1987－1990.］

［3］ZHOU Chuanhua，QIAN Feng.Improvement of quantum genetic algorithm and its application ［J］.Computer Applications，2008，28 （2）：286－288（in Chinese）.［周传华，钱锋.改进量子遗传算法及其应用［J］.计算机应用，2008，28 （2）：286－288.］

［4］GAO Yinghui，SHEN Zhenkang.An angle－coding chromosome quantum genetic algorithm ［J］.Computer Engineering＆Science，2009，31 （3）：75－79 （in Chinese）.［高颖慧，沈振康.角度编码染色体量子遗传算法 ［J］.计算机工程与科学，2009，31 （3）：75－79.］

［5］LI Shiyong，LI Hao.Quantum genetic algorithm based on phase comparison ［J］.Systems Engineering and Electronics，2010，32 （10）：2219－2222 （in Chinese）.［李士勇，李浩.一种基于相位比较的量子遗传算法 ［J］.系统工程与电子技术，2010，32 （10）：2219－2222.］

［6］XU Bo，PENG Zhiping，YU Jianping.Improved quantum genetic algorithm based on cloud model theory［J］.Application Research of Computers，2011，28 （10）：3684－3686 （in Chinese）. ［许 波，彭志平，余建平.一种基于云模型的改进型量子遗传算法 ［J］.计算机应用研究，2011，28 （10）：3684－3686.］

［7］SHA Linxiu，HE Yuyao，CHEN Yanwei.Variable step double chains quantum genetic algorithm ［J］.Computer Engineering and Applications，2012，48 （20）：59－63 （in Chinese）.［沙林秀，贺昱曜，陈延伟.一种变步长双链量子遗传算法［J］.计算机工程与应用，2012，48 （20）：59－63.］

［8］LIU Weining，JIN Hongbing，LIU Bo.Cloud computing resource scheduling based on improved quantum genetic algorithm［J］.Journal of Computer Applications，2013，33 （8）：2151－2153 （in Chinese）. ［刘卫宁，靳洪兵，刘波.基于改进量子遗传算法的云计算资源调度 ［J］.计算机应用，2013，33（8）：2151－2153.］

［9］CUI Wenhua，LIU Xiaobing.Survey on shuffled frog leaping algorithm ［J］.Control and Decision，2012，27 （4）：481－486（in Chinese）. ［崔文华，刘晓冰.混合蛙跳算法研究综述［J］.控制与决策，2012，27 （4）：481－486.］

［10］WANG Yinnian，GE Hongwei.Improved simulated annealing genetic algorithm for solving TSP problem ［J］.Computer Engineering and Applications，2010，46 （5）：44－47 （in Chinese）.［王银年，葛宏伟.求解TSP问题的改进模拟退火遗传算法 ［J］.计算机工程与应用，2010，46 （5）：44－47.］