基于最优保留策略的改进遗传算法

梁兴建，詹志辉，谭 伟，彭建新

（1.四川理工学院 计算机学院，四川 自贡643000；2.中山大学 计算机科学系，广东 广州510006；3.东莞理工学院 计算机学院，广东 东莞523106；4.广东警官学院 计算机系，广东 广州510230）

0 引 言

遗传算法 （genetic algorithm，GA）过程简单、易于操作，具有较强的健壮性和普适性，在多个领域取得了成功的应用。但是作为以群体进化为基础的算法，收敛速度慢和易早熟收敛两个缺陷不可避免［1－8］。因此，改进遗传算法成为近年来研究的热点，改进策略可归结为以下几个方面：对选择算子的改进［3，4］、对交配算子的改进［5］、对变异算子的改进［6］、对交配和变异参数自适应控制［7］、与其它优化算法混合［2，8，9］等。从文献结果上看，大多数改进方法对加快收敛速度和提升求解精度都有一定帮助，但是有的改进方法对求解精度的提高仍然不大，有的则花费较大的系统开销来提升算法效果，遗传算法在上述问题中还有较大的改进空间。

为了进一步提升收敛速度和提高解的精度，本文提出了一种基于最优保留策略的改进遗传算法 （elitist reserved GA，ERGA），算法首先对选择算子进行改进，在进化过程中加强个体优胜劣汰的思想，保障最优个体的基因能迅速向后代传播，从而使整个群体逐步朝着最优方向发展。然而，保留最优个体策略通常存在种群多样性快速降低的问题。因此，本文在保留最优策略的基础上进一步通过对变异算子的优化，不断产生优质基因，既能提高个体的适应值，又能提升种群多样性。本文提出的改进遗传算法通过对选择算子和变异算子的改进，能更好地平衡算法收敛性和多样性，在保证种群多样性的同时加快算法的收敛速度，最终能快速找到高质量的解。本文对8个基准测试函数进行了仿真实验，数据的比较和分析结果表明，本文改进算法在收敛速度与全局寻优上有较大的改善。

1 遗传算法的基本思想

作为生物进化论和遗传规律在计算机上的模拟，标准遗传算法 （standard GA，SGA）主要涉及染色体编码、群体初始化、适应值评价、种群选择算子、染色体交配算子、变异算子等概念。

（1）染色体编码

染色体通常用于表示问题的解空间，染色体编码方法主要有：雷格码编码、字母编码、二进制编码、浮点数编码、多参数交叉编码等，根据不同的问题采用不同的编码方式。本文用于求解函数优化问题，因而采用浮点数编码，此时，染色体的长度为问题定义的解的变量个数，每个基因即为每一维变量，如待求解问题的一个有效解为Xi＝ （，，…，，），其中D 为变量的维数（即染色体长度），则该解的对应的染色体编码为（，，…，，）。

（2）群体初始化

初始化是对染色体的每一个基因赋初值，通常采用的是随机数初始方法，依次为染色体每一维变量设定初始值，初始值应处于一个合理的空间范围。假设上述问题的每一个维度的搜索范围都是 ［－10，10］，则某个染色体初始值随机取值可能为Xi＝（3.21，－4.18，…，－6.25，2.47）。

（3）适应值评价

适应值评价主要是通过评估函数计算各个染色体的适应值，从而区分染色体的优劣，评估函数通常根据问题的优化目标来确定［10］。对于求解函数优化问题，直接可利用问题定义的目标函数作为评估函数的原型。由于标准遗传算法采用轮盘赌的方法对种群进行筛选，因此染色体的适应值越大越容易被选择。然而本文主要针对最小值优化的函数进行求解，因此对于此类目标函数f（X），应采用取负数、取倒数等方式得到评估函数Eval（C），为了使后一步轮盘赌的概率更合理，本文采用文献 ［11］提供的公式计算适应值

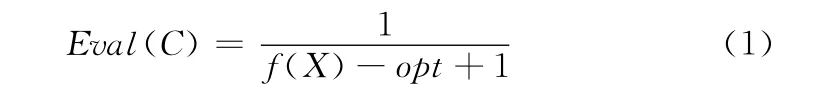
式中：X——一个有效解，C——X 对应的染色体，op——f（X）的理论最小值。

（4）种群选择算子

种群的选择是一个非常重要的步骤，需要从现有种群择优选出下一代染色体的群体 ｛C1，C2，C3，…，Cn｝，原则是既要保证让下一代的种群更优，又要保证种群多样化。通常的选择算法有轮盘赌选择算法、锦标赛选择算法等。轮盘赌选择的核心思想是根据染色体的适应值，计算出每个染色体适应值与群体种适应值总和的比P，然后以P 为概率随机选择下一代种群。锦标赛选择的核心思想则是，一次随机抽出若干个染色体，并将这组染色体中适应值最大的一个选入下一代。这2种选择算子各有优缺点，轮盘赌选择的优点是根据随机概率，既能保证优先选择适应值大的，又能给较差的染色体一些生存空间，但事实上，由于选择的随机性，可能最优的染色体一次都没有选择，而最差的却多次被选择。锦标赛选择能最大的保证优胜劣汰，但是由于适应值较小的染色体淘汰速度过快，而容易使种群多样化迅速减小从而产生早熟。本文结合保留最优策略和轮盘赌选择方法对种群选择算子进行改进。

（5）染色体交配算子

染色体根据交配概率Pc决定是否参与交配，不参与的直接放入下一代，需参与交配的，每2个染色体交换各自的部分基因形成2个新的子代染色体。交配算子的改进主要从2个方面进行：其一是交配概率Pc的取值，Pc一般取值0.4～0.99，也有研究人员采用自适应方法在运行过程中临时调整Pc值；其二是交配方式，主要有单点交配、多点交配、均匀交配、循环交配等。本文对交配概率Pc采用固定值，交配方式采用随机单点交配。

（6）种群变异算子

在交配过程结束后，所有染色体根据变异概率Pm决定是否变异，需要变异的染色体，随机抽取一个位置的基因，将其数值改为新的随机值。变异的优点是能提高种群的多样性，有效防止早熟，但是在已经有较优解的时候，随意变异常常又会使结果变差。因此变异概率Pm通常设为0.001～0.1之间，本文改进的另一个重点就是如何让变异既能防止早熟，又能使子代变得更优。

2 改进具体方案

本改进算法的思路是基于最优保留策略对选择算子进行改进，然后采用对变异算子的优化，在全局范围不断探索最优解，并且保持种群多样性。本算法的总体流程如图1所示。

2.1 基于最优保留策略的改进选择算子

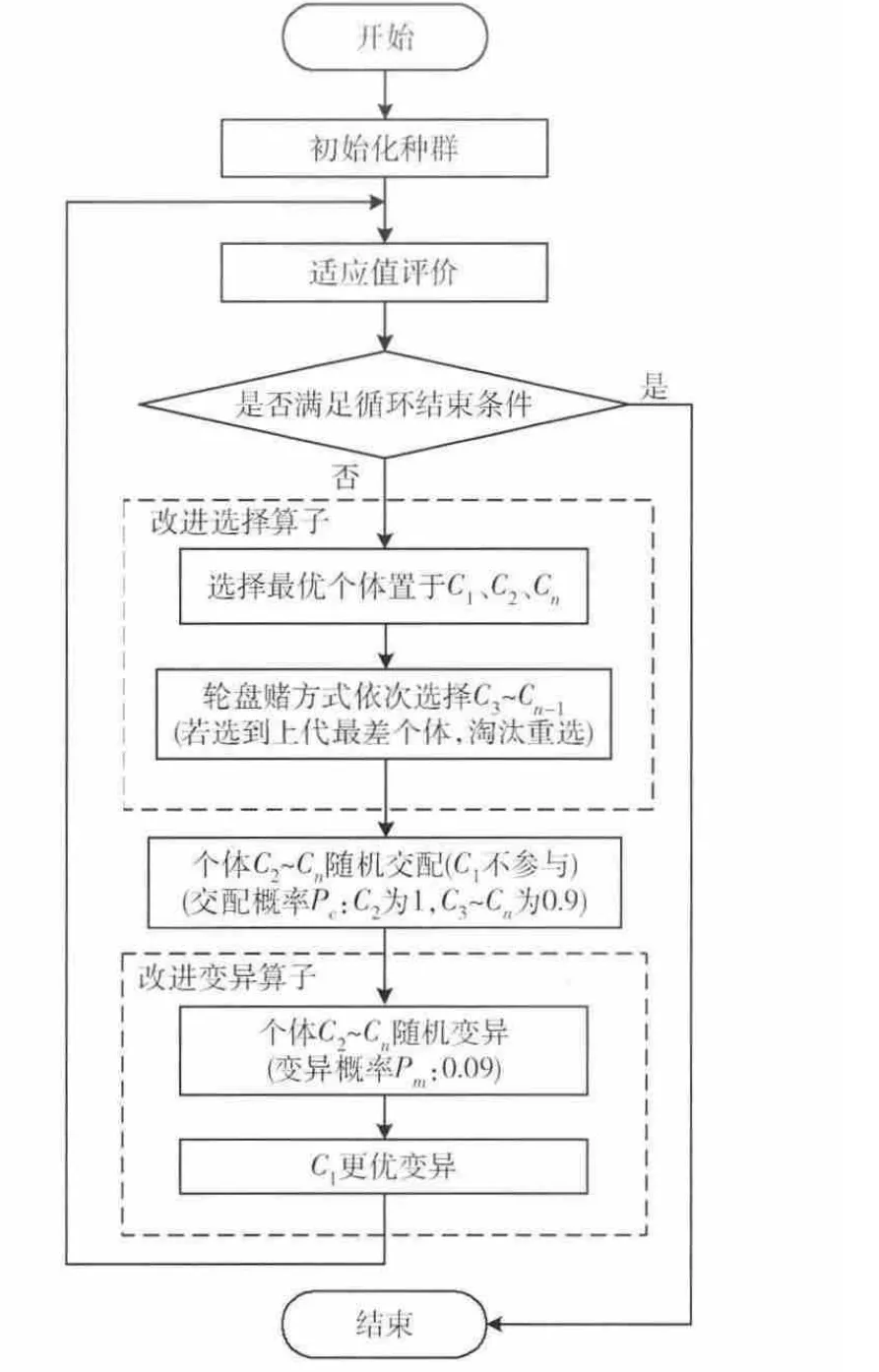
图1 改进遗传算法总体流程

采用常规轮盘赌选择过程，从概率角度上看，个体被选择机会与适应值高低成正比，适应值高的选择机会大，适应值低的也有一定的被选择的机会。但事实上由于个体选择概率具有不准确性和选择过于随机性，可能导致最优个体一次都没有选上，而较差个体却被选上多次。这与生物进化理论背道而驰，因此本算法在新群体选择中注重优胜劣汰思想，使群体朝着更优化的方向发展。选择过程改进思路如下：

（1）保留最优个体策略

为了有效保留上一代的最优个体，并能让最优个体参与交配，以探索出更优个体，改进以往保存最优的策略，要求C1、C2、Cn都选择上一代的最优个体，其中：C1不参与交配，主要用于保存上代最优个体并完成更优变异；C2将必须参与交配；Cn按交配概率Pc参与交配。C2与Cn分开是为了将上代最优个体的优秀基因散播得更广。

（2）其它个体选择策略

对新的 ｛C3，C4，…，Cn－1｝个体群，采用轮盘赌方式依次选择，但如果选择到上一代最差个体，则放弃重选，以达到优胜劣汰的目的。选择后的 ｛C3，C4，…，Cn－1｝个体群将按交配概率Pc决定是否参与交配。

2.2 变异算子改进

在个体交配完毕之后，需要对某些个体进行变异操作。采用常规变异方法，由于数据取值范围大，如果变更某个体的基因太过随机，反而会造成个体的适应值变低，尤其是随着进化代数的增加，随机变异所起的负面作用将越来越高，因此通常采用降低遗传概率Pm来解决这个问题，但降低遗传概率实际上也会降低种群数量，导致早熟收敛。

为了解决此矛盾，本算法除了常规变异以外，还针对上一代最优个体C1进行优化变异，使该个体适应值能优于上一代，从而加快收敛速度。变异过程改进思路如下：

（1）首先对群体 ｛C2，C3，…，Cn｝依次变异，按照变异概率Pm随机选择参加变异的个体，在随机位置进行基因修改，这有利于搜索到更好地基因，又不会造成对最优个体的破坏；

（2）C1保存的是上一代最优个体，进行优化变异，变异过程通过以下4个步骤完成：

步骤1 确立变异基因位置。C1本是保留的上代最优个体，随机位置变异很容易造成适应值降低，因此对最优个体不再适合采用随机位置变异，同时为了使C1在前几代变异的基因得以保留，本改进采用基因循环变异方式，即选择上一代结束变异位置Lflag作为本次变异初始位置Lmutate。

步骤2 重新确定变异数据搜索空间S。为了避免全局范围盲目取值破坏到优秀基因，本算法对取值范围逐渐缩减，即首先在整个群体中搜索Lmutate位置的基因最小值gmin和最大值gmax。由gmin和gmax构成搜索空间，能很大程度地缩小范围，但随着进化代数的增加，很容易收敛到局部最优 （即gmin＝gmax）。为了避免该问题，通过式 （2）、式（3）将搜索范围的进行扩大，得到最终的搜索空间为S∈（rangemin，rangemax）

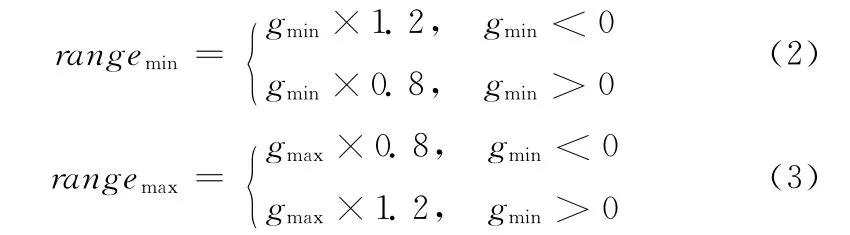
步骤3 得到变异数据并执行变异。在搜索空间S 中随机得到一个变异数据r，由数据r去替换Lmutate位置的基因数据。

步骤4 确定变异是否成功。通过步骤3 执行变异之后，对个体C1进行一次适应值评价，并与上一代最优适应值Vmax比较，若优于Vmax，则变异成功，记录本代变异位置为Lflag＝Lmutate＋1，结束整个变异过程；反之，若变异之后适应值比上一代更差，则先将该位置基因还原，调整变异位置Lmutate＝Lmutate＋1，转向步骤2对下一位置的基因进行变异，直到所有基因都试探过，回到初始位置 （即Lmutate＝Lflag），则本次变异失败，结束整个变异过程。

3 实验验证和结果对比

3.1 基准函数说明

表1列出了用于实验测试的8 个基准函数［4］，这些函数可分为2组，前4个为是单峰函数，后4个是多峰函数，其中多峰函数存在多个局部最优解。另外，在表1中还给出了测试的基因维数D （第三列），基因数据的搜索空间（第四列），该函数对应的全局最优值fmin（第五列），由于进化计算是不确定算法，对每个函数都设定了可接受精度（第六列），如果能够得到介于可接受值和最佳值之间的结果，都可判定为成功，最后一列是函数的名称。

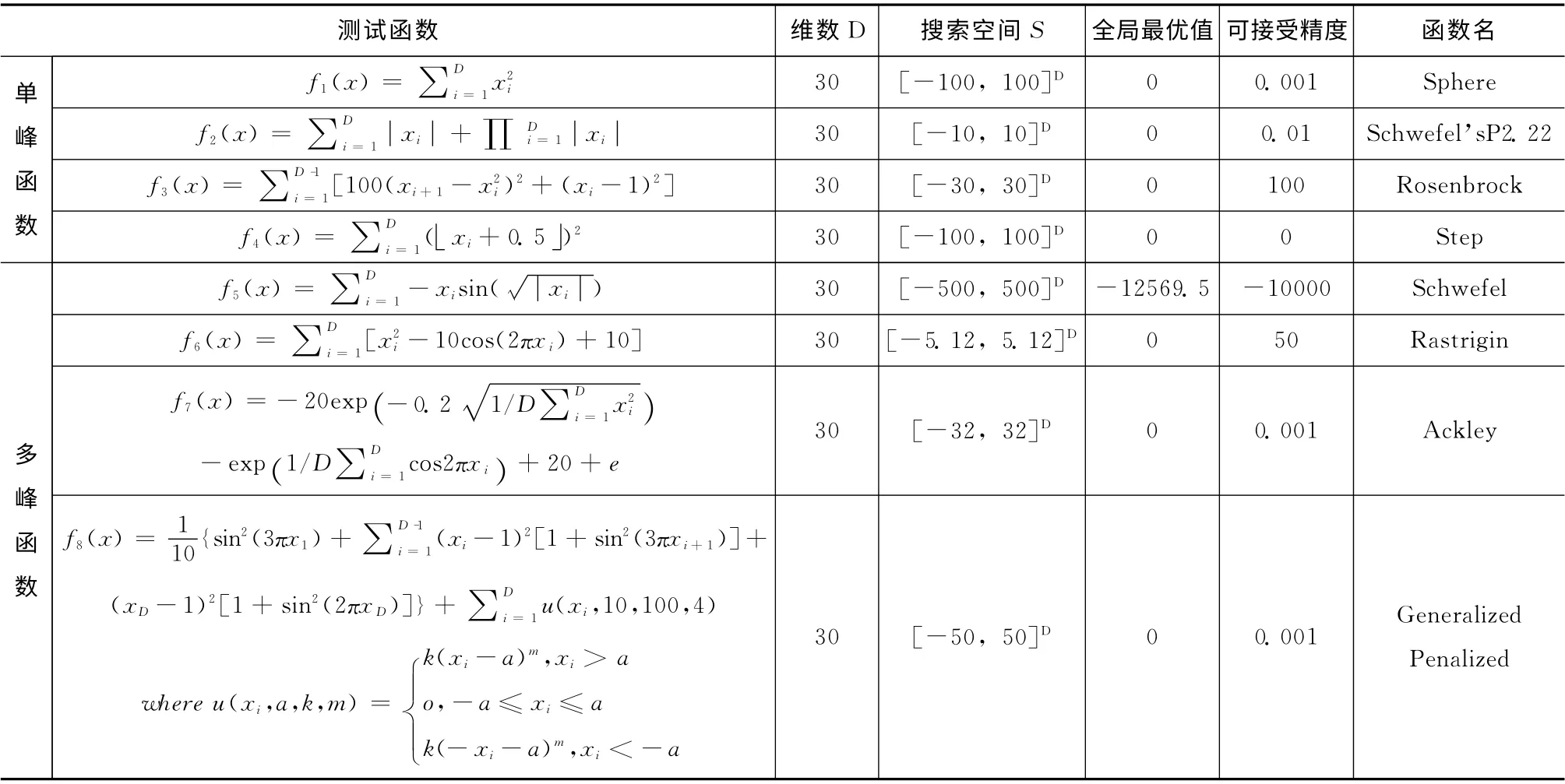
表1 用于实验测试的8个基准函数

由于本改进在完成变异的时候会多次调用适应值评价函数，而调用适应值评价函数消耗系统资源量较大，因此为了公平的与其它算法比较，所有算法都采用最大适应值评价次数为100万次作为循环结束条件。同时，为了减少统计误差，每个算法在每个函数上测试30次，分别取出最优值、平均值、最差值进行比较。

3.2 结果比较与分析

为了对比本改进算法的优化程度，将本算法 （ERGA）的运行结果与标准遗传算法 （SGA）、文献 ［4］提出的改进算法 （命名为improved GA，IGA）的结果进行比较。本比较所采用的测试函数、停止准则均与文献［4］相同，其中每个函数对应搜索空间详见表1、基因长度 （维数）都为30、群体规模都为50、结束条件都为评价100 万次，ERGA 和SGA 的非特殊交配概率Pc为0.9、变异概率Pm为0.09，通过运算30 次统计出平均值、最优值、最差值，实验结果见表2，其中IGA 的结果是由文献 ［4］提供的，表2中粗体显示的数据是3种算法运行结果的最优值。

从表2单独看本改进算法 （ERGA）的数据情况，ERGA 对单峰函数的收敛总体上要优于多峰函数，单峰函数f4能收敛到全局最优、f1达到10－50数量级、f2接近10－30数量级，多峰函数除f5外都在10－10数量级左右。

从表2对3种算法结果的数据情况比较，ERGA 除了对多峰函数f5的改进效果不如IGA 外，对其它的函数的改进都有较好的效果，同等情况下精确程度能提高多个数量级。尤其对f1函数，SGA 和IGA 的精度最多只能达到10－4数量 级，而ERGA 能 达 到10－50数 量 级。另 外，应 用ERGA 算法对f2函 数 能 收 敛 到10－30数 量 级 （SGA 和IGA只能达到10－2数量级），ERGA 算法对f6～f8函数均能收敛到10－10数 量 级 （SGA 是10－3数 量 级，IGA 是10－4数 量级），对f3函数虽然数量级没有提升，但是结果精度也远高于IGA 和SGA，经以上数据比较，说明本改进是有利于提升遗传算法性能的。

图2 和图3 是基本遗传算法 （SGA）和本改进算法（ERGA）对8个测试函数 （f1～f8）的求解变化趋势，图中横坐标是运行过程中评估函数的调用次数，纵坐标是相关评估次数对应的结果，由于大部分函数在进化前后期所得结果数量级差距太大，为了便于观察和对比2种算法的收敛情况，除了f5函数外，都以10的数量级作为纵坐标。

图2是基本遗传算法 （SGA）和本改进算法 （ERGA）对单峰函数函数f1～f4的求解变化趋势，从图中可以清晰的看到，SGA 要么收敛速度慢 （如：f4），要么陷入局部最优 （如：f1～f3），而ERGA 除f3函数外，其余函数都没有陷入局部最优，f1和f2函数一直处于加速寻优状态，f4函数收敛速度最快，在7万次评估 （约1000代）左右快速得到全局最优值0。

图3是SGA 和ERGA 对多峰函数f5～f8的求解变化趋势，通过对比可发现，4个多峰函数应用SGA 算法都存在过早收敛、求解精度不高的情况，而应用ERGA 算法，f6和f7函数在评估60 000 次之后出现加速寻优的情况，f8虽然在评估60 000次之后开始收敛，但是结果精确度数量级已远远高于SGA。

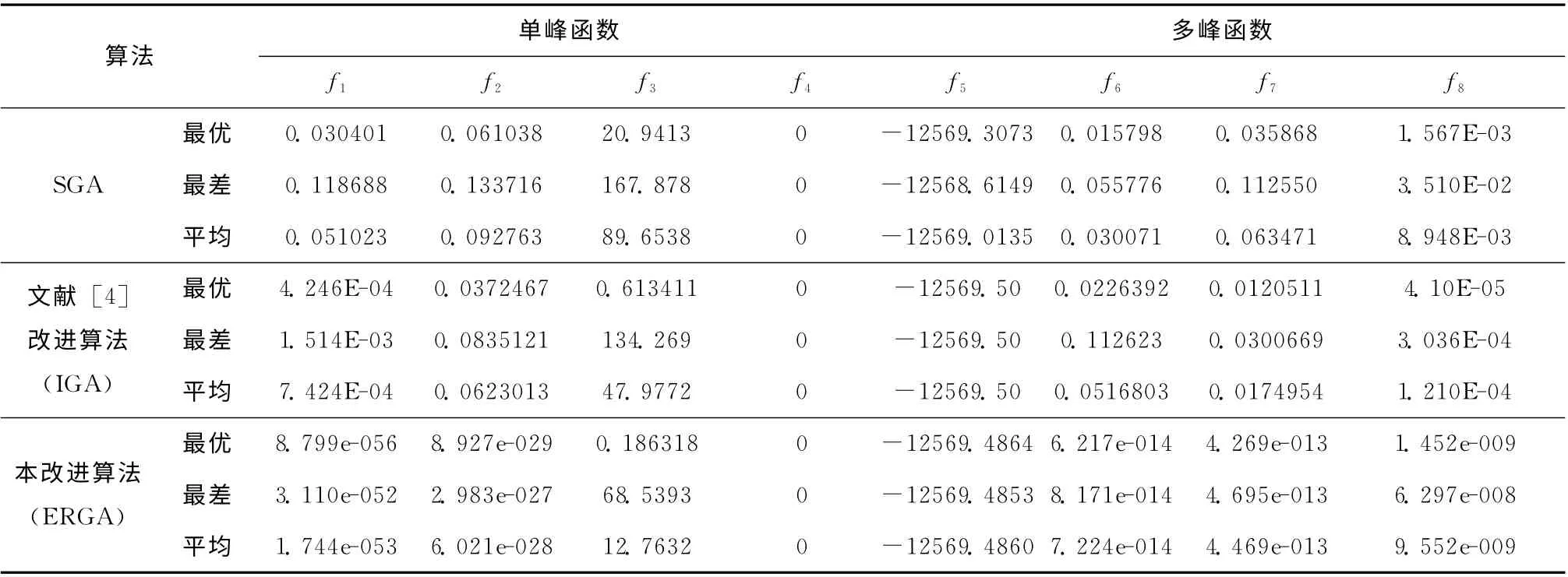
表2 SGA、IGA 和ERGA 求解函数实验结果比对

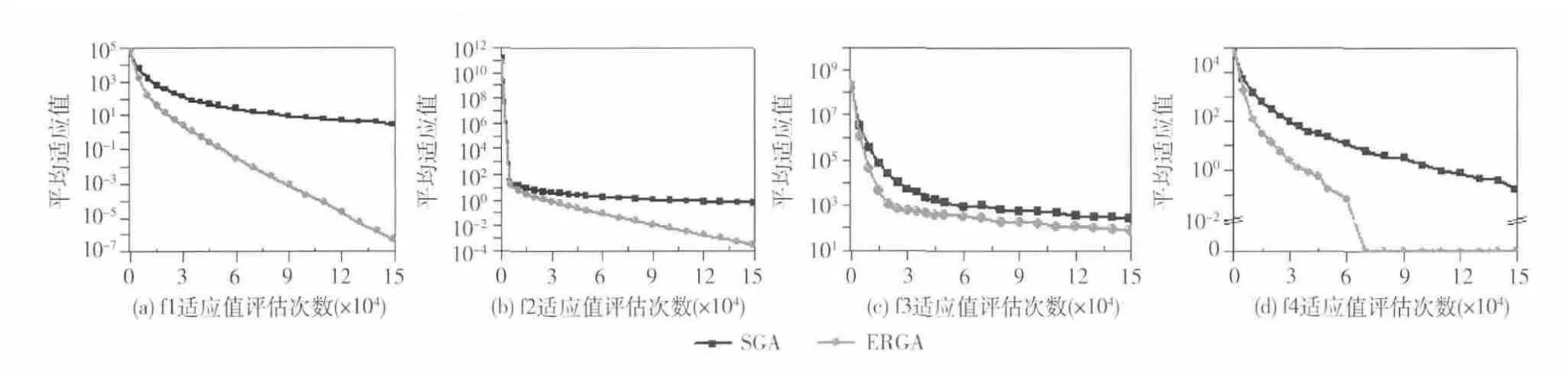
图2 SGA 和本改进算法 （ERGA）对单峰函数函数f1～f4 的求解变化趋势

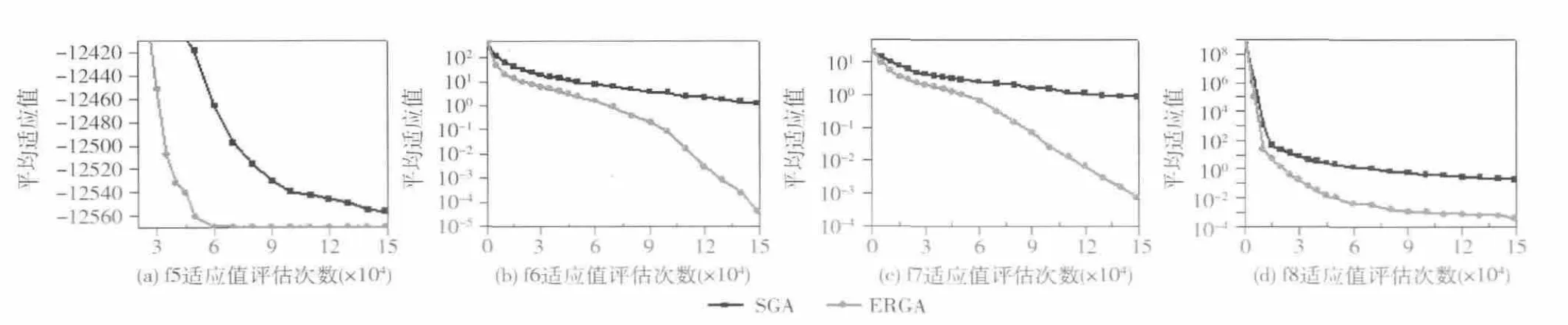
图3 SGA 和本改进算法 （ERGA）对多峰函数f5～f8 的求解变化趋势

4 结束语

为了解决遗传算法收敛速度慢和收敛早熟2 个问题，本文提出了一种基于最优保留策略的改进遗传算法，该算法同时对选择算子和变异算子进行改进。选择算子采用保留最优策略实现了群体优胜劣汰，变异算子采用最优个体优化变异思想，用以解决保留最优带来的种群下降问题，同时提升结果精度。通过对8个基准函数 （包括单峰、多峰函数各4个）进行测试对比，实验结果表明本改进算法收敛速度快，求解精度高，对大多数函数都能避免陷入局部最优，对遗传算法的性能有较大的提升。在后续研究中，我们将尝试使用自适应控制的方法［12］和正交实验设计方法［13］对ERGA 进行进一步的性能提升，并尝试将ERGA在多目标等优化问题中［14］进行应用。

［1］ZHANG Jun，ZHAN Zhihui.Computational intelligence［M］.Beijing：Tsinghua University Press，2009：54－58 （in Chinese）.［张军，詹志辉.计算智能 ［M］.北京：清华大学出版社，2009：54－58.］

［2］YAN Taishan.An improved genetic algorithm and its blending application with neural network ［C］／／Second International Workshop on Intelligent Systems and Applications，2010：9－12.

［3］Amarita Ritthipakdee，Arit Thammano，Nol Premasathian，et al.A new selection operator to improve the performance of genetic algorithm for optimization problems ［C］／／IEEE ICMA Conference International Scientific Advisory Board，2013：371－375.

［4］CHEN Youqing，XU Caixing，ZHONG Wenliang，et al.Genetic algorithm with improved selection operator［J］.Computer Engineering and Applications，2008，44 （2）：44－49 （in Chinese）.［陈有青，徐蔡星，钟文亮，等.一种改进选择算子的遗 传 算 法 ［J］.计 算 机 工 程 与 应 用，2008，44 （2）：44－49.］

［5］Zhang Qiyi，Chang Shuchun.An improved crossover operator of genetic algorithm ［C］／／Second International Symposium on Computational Intelligence and Design，2009：82－86.

［6］SilvaFJM da，Sanchez PerezJM，Pulido JAG，et al.Optimizing multiple sequence alignment by improving mutation operators of a genetic algorithm ［C］／／Ninth International Conference on Intelligent Systems Design and Applications，2009：1257－1262.

［7］ZHANG Jingzhao，JIANG Tao.Improved adaptive genetic algorithm ［J］.Computer Engineering and Applications，2010，46 （11）：53－55 （in Chinese）.［张京钊，江涛.改进的自适应遗传算法 ［J］.计算机工程与应用，2010，46 （11）：53－55.］

［8］YANG Chao，WANG Zhengyong，WU Xiaohong.A core image matching algorithm based on chaos genetic algorithm and wavelet multi－resolution analysis［J］.Journal of Sichuan Uni－versity of Science ＆ Engineering （Natural Science Edition），2010，23 （6）：704－706 （in Chinese）. ［杨超，王正勇，吴晓红.基于混沌遗传算法与小波多分辨率分析的岩心图像匹配［J］.四 川 理 工 学 院 学 报 （自 然 科 学 版），2010，23 （6）：704－706.］

［9］XING Xiaoshuai，CHEN Yanfang，ZHOU Li，et al.A parallel immune genetic algorithm Based on simulated annealing［C］／／International Conference on Multimedia Technology，2011：3366－3369.

［10］HE Qing，ZENG Huanglin，XIONG Xingzhong.Research on cross－layer resource allocation for OFDMA system based on genetic algorithm ［J］.Journal of Sichuan University of Science ＆ Engineering （Natural Science Edition），2012，25（5）：45－49 （in Chinese）.［何庆，曾黄麟，熊兴中.一种基于遗传算法的OFDMA 系统的跨层资源分配 ［J］.四川理工学院学报 （自然科学版），2012，25 （5）：45－49.］

［11］ZHANG Chen，ZHAN Zhihui.Comparisons of selection strategy in genetic algorithm ［J］.Computer Engineering and Design，2009，30 （23）：5471－5478 （in Chinese）. ［张琛，詹志辉.遗传算法选择策略比较 ［J］.计算机工程与设计，2009，30 （23）：5471－5478.］

［12］ZHAN Zhihui，Zhang Jun，Li Yun，et al.Adaptive particle swarm optimization ［J］.IEEE Transactions on Systems，Man，and Cybernetics－Part B，2009，39 （6）：1362－1381.

［13］ZHAN Zhihui，Zhang Jun，Li Yun，et al.Orthogonal learning particle swarm optimization ［J］.IEEE Transactions on Evolutionary Computation，2011，15 （6）：832－847.

［14］ZHAN Zhihui，Li Jingjing，Cao Jiannong，et al.Multiple populations for multiple objectives：A coevolutionary technique for solving multiobjective optimization problems ［J］.IEEE Transactions on Cybernetics，2013，43 （2）：445－463.