Thermoelectric Properties of the CuGaTe2 Crystal from First-principles Calculations: the Role of Doping and Temperature①

ZHAO Xio-ChunSUN Bo-Zhen HE Cho MA Zu-Ju LI Qio-Hong WU Ke-Chen



Thermoelectric Properties of the CuGaTe2Crystal from First-principles Calculations: the Role of Doping and Temperature①

ZHAO Xiao-Chuana, bSUN Bao-ZhenaHE ChaoaMA Zu-JuaLI Qiao-HongaWU Ke-Chena②

a(350002)b(100049)

The thermoelectric properties of CuGaTe2crystal are investigated by using the first-principles method and semi-classical Boltzmann theory. We find that the electronic structure of CuGaTe2is favorable for-type doping. The transport coefficients can be tuned by doping and changing the work temperature to yield an optimized thermoelectric performance. The optimal doping concentration is 2×1020cm-3, in which the maximum ZT value can reach 1.65 at 900 K. The results suggest CuGaTe2might find promising applications as good thermoelectric materials, particularly at high temperature.

thermoelectric material,-type doping, density functional theory

1 INTRODUCTION

Energy-related issues are becoming more and more crucial. Devices based on thermoelectric (TE) materials are very appealing in this context. They can convert waste heat into usable electricity[1]. The technology of energy conversions from waste heat into electrical energy is very important for develo- ping alternative energy technologies to reduce our dependence on fossil fuels[2]. Recently, some kinds of efficient thermoelectric materials have been developed, such as Bi2Te3and its alloy[3]. However, the efficiency of those materials is still not high enough, which limits their applications. Therefore, there are now considerable demands in identifying new materials with more enhanced thermoelectric performance.

The efficiency of thermoelectric materials is defined by the dimensionless figure of merit (ZT), ZT = S2σT/κ, where S, σ, T and κ are the Seebeck coefficient, electrical conductivity, absolute tempe- rature and thermal conductivity, respectively. It is clear that a small κ will lead to a high ZT, which means a high efficiency of the thermoelectric materials. It provides us a clue to find good thermo- electric materials. Among the existing materials, some compounds of chalcopyrite structure were found to have a small κ[4]. It encourages us to find excellent thermoelectric materials from compounds with similar structures. Indeed, AgGaTe2has been reported to exhibit a large ZT value of 1.19 at 900 K in our previous study[5]. CuGaTe2compound is also expected to be a possible thermoelectric material because of the similarity of its crystal structure to that of chalcopyrite. In theory, Gudelli et al. inves- tigated the thermoelectric properties of CuGaTe2in the temperature range of 700～950 K[6]. In fact, typical thermoelectric power generation modules operate anywhere from 300 to 1000 K. On the other hand, doping is still an effective approach to enhan- ce the thermoelectric performance of compound[7]. For example, Kurosaki et al. revealed that doped Ag0.95GaTe2has value of ZT around 0.7[8]. However, for CuGaTe2, the optimal temperature and doping concentration have not been given yet. Therefore, in order to improve the ZT value, it is necessary to have a better understanding of the dependence of the thermoelectric properties of CuGaTe2on the doping concentration and working temperature.

In this paper, we performed the first-principles computation on the doping and temperature depen- dence of the thermoelectric properties of CuGaTe2. In particular, the doping concentration is from 1018to 1021cm-3and the temperature falls in the range of 300～1000 K. Our calculations show that the-type doped CuGaTe2with proper carrier concentration is a promising thermoelectric material.

2 COMPUTATIONAL DETAILS

The crystal structure of CuGaTe2is shown in Fig. 1. It contains 4 Cu, 4 Ga and 8 Te atoms. The space group is42. The calculated lattice parameters are== 5.932 and= 11.837, which are in accordance with the experimental data (== 6.028,= 11.949)[9].

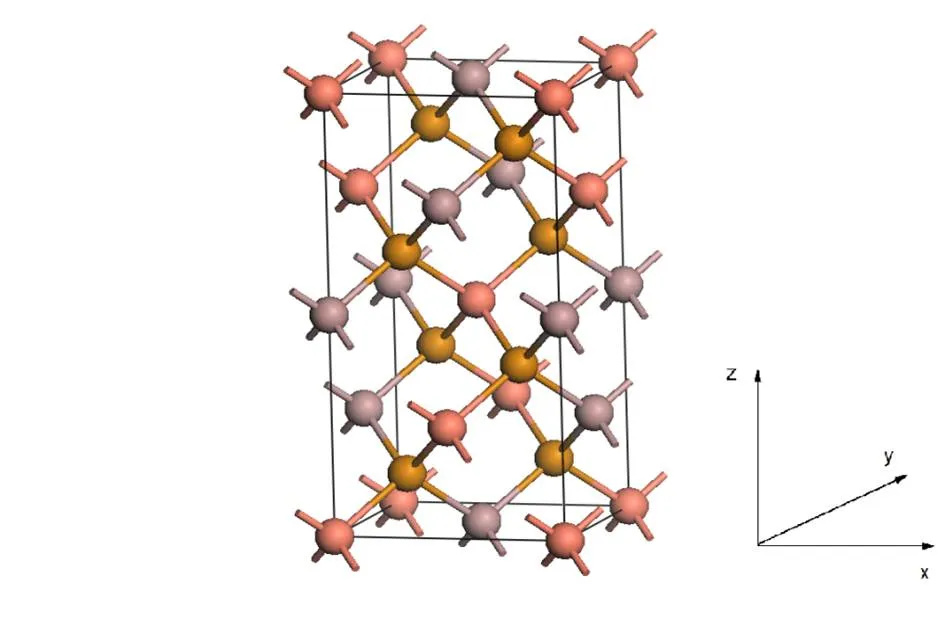
Fig. 1. Crystal structure of CuGaTe2. Cu, Ga, and Te atoms are colored in pink, purple, and yellow, respectively

The electronic structure calculations were perfor- med by using first-principles method implemented in the VASP software package[10]. The projector augmented wave (PAW)[11]potentials are used to describe the interaction between electron and ion. Local density functional (LDA)[12]is employed to describe the exchange and correlation function. Test of energy cutoffs shows that 400 eV is ideal for the following calculations. The Brillouin zone integra- tion was sampled using 5 × 5 × 5 of Monkhorst-Pack k-point grids in the structural relaxation and the self-consistent total energy calculations. It is known that the value of band gap resulted from the DFT theory is always smaller than that from experimental data. And it results in relatively lower Seebeck coefficients[13-15]. Based on the ε(n, k) resulted from DFT calculation, the Seebeck coefficient is available by solving Boltzmann Equation using BOLTZTRAP code[16]. The Seebeck coefficient is calculated as follows.

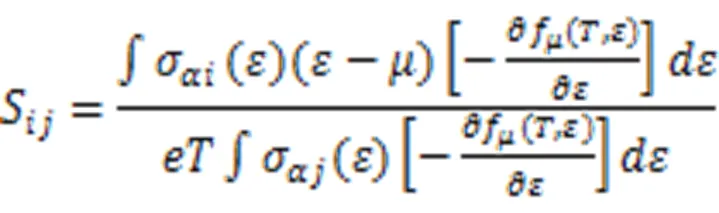
If off-diagonal elements are neglected, then:

In this equation, Fermi-Dirac distribution function:

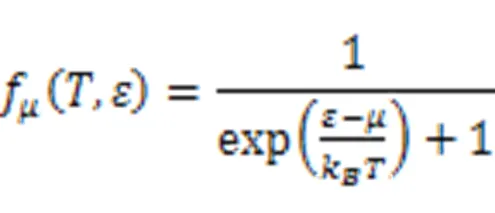
Conduction sensor:

Andis the chemical potential,kthe Boltzmann constant andthe group velocity.

We adopted rigid band approximation[13]. In this approximation, it assumes that the doping density has no relationship with the band structure, while it only has an influence on the Seebeck coefficient. To find out the best condition, the temperature scale should be wide enough to include the best temperature. So, the temperature is set between 300 and 1000 K with the interval to be 100 K.

3 RESULTS AND DISCUSSION

Fig. 2 shows the calculated result of the band structure of CuGaTe2. Obviously, CuGaTe2is a direct band semiconductor. The calculated band gap value (0.439 eV) is nearly 1 eV smaller than the experimental value of 1.38 eV[17], which is ascribed to the underestimated band gap through DFT calculation. We can also see the mixture of heavy and light bands around the top of the valence band.

Fig. 2. Band structure of CuGaTe2

The projected density of states (PDOS) and total density of states (TDOS) of CuGaTe2are shown in Fig. 3. From Fig. 3 we can see that the valence and conduction bands in this compound have different characters. The valence bands are primarily derived from Cu component, whereas the contribution of Ga component to this part can be neglected. The conduction bands are contributed from Ga and Te components, respectively. Moreover, several apparent peaks are observed in the range from 0 to –2 eV. These characters are favorable for-type doping, which is consistent with the result obtained by Gudelli et al[6]. So, only-type doped CuGaTe2was discussed in the following calculations.

Fig. 4a shows the calculated Seebeck coefficients (S) at different doping concentration and tempe- rature. The Seebeck coefficients are strongly depen- dent on the temperature and carrier concentration. For the same temperature, the Seebeck coefficient decreases as n grows up, but for the same n above 2.1´1018cm-3, the Seebeck coefficient increases with the increase of T. At high temperature, S is still large under heavy doping concentration. For example, when T = 1000 K and n = 1019～1020cm-3, S is still in the range of 150～240mV/K. Therefore, we can infer that the largest ZT of CuGaTe2would be reached at high temperature and relatively high doping density, and this is proved to be true by the following analysis.

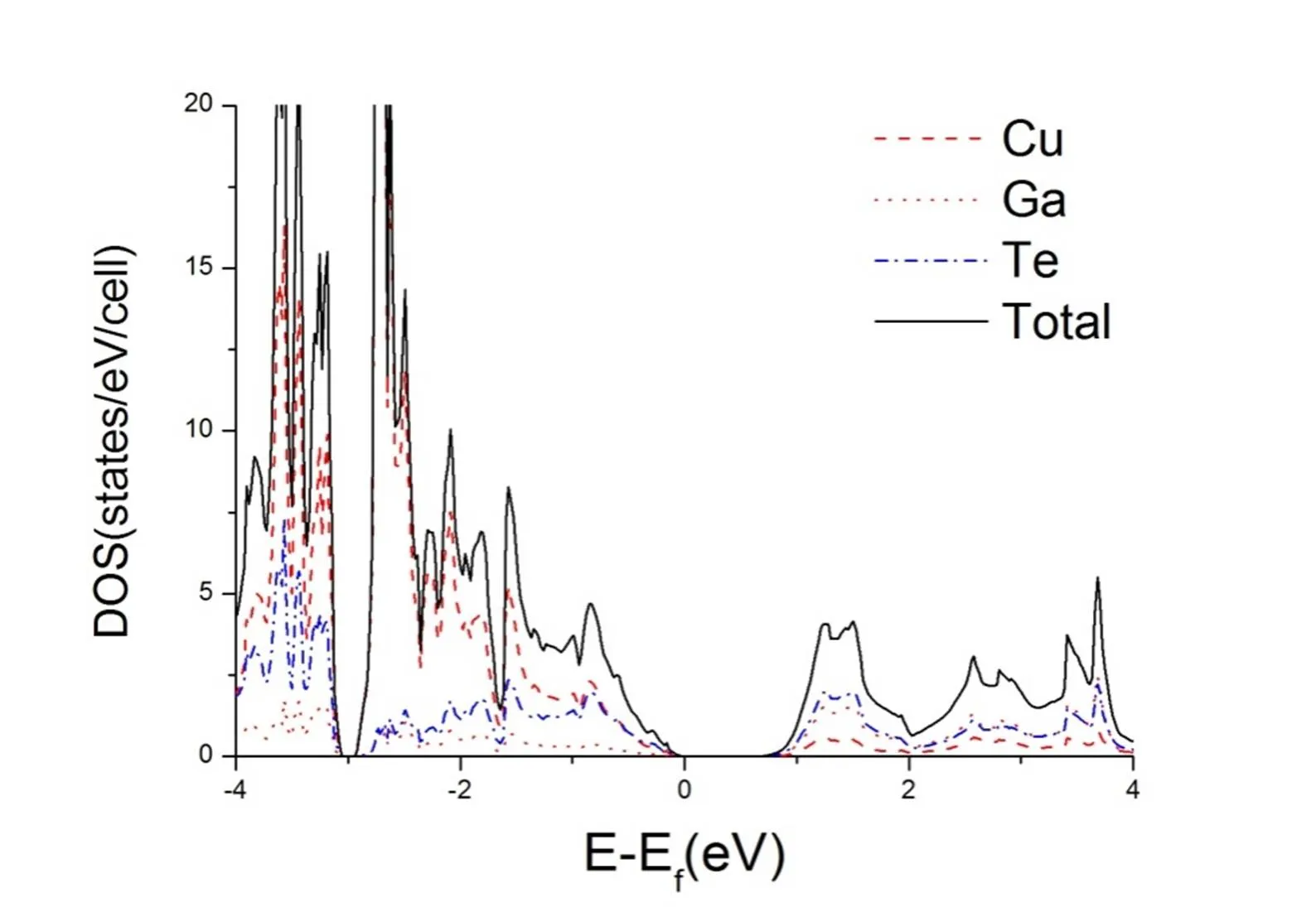
Fig. 3. Projected density of states (PDOS) and total density of states (TDOS) of CuGaTe2

Fig. 4. Caculated TE properties for-type doped CuGaTe2as a function of T and n: (a) seebeck coefficient, (b) electrical conductivity, (c) power factor, and (d) ZT

Using the electronic structure, it is possible to calculate σ/τ as a function of n and T, but it is impossible to calculatesitself without the knowle- dge of the scattering rate τ-1. In order to proceed with the calculations, we assume that τ is in the typical electron-phonon form, τ = AT-1n1/3(τ in s, T in K, n in cm-3)[14]. In this work, we just take the relaxing time τ as a constant at the given temperature[6]. And the data of the relaxing time τ come from Ref. 18[18]. Then we obtain the n-dependentsas is shown in Fig. 4b. Due to stronger scatter for higher temperature,sof CuGaTe2with the same carrier concentration (n is above 5´1018cm-3) decreases as the temperature increases. But at the same temperature,sincreases as n increases from 1018to 1021cm-3.

The calculated power factor S2sis presented in Fig. 4c. At 800 K, the power factor reaches the maximum, which is 1.39 mW/mK2. At 900 K, the power factor is 0.92 mW/mK2, in good agreement with the experimental finding (1.05 mW/mK2)[18]. The optimal carrier concentration is about 2.0´1020cm-3for all temperature. Such doping concentration is probably experimentally controllable.

According to the result of Singh[19], the doping concentration has little influence on the thermal conductivity and, thus we believe that κ depends only on the temperature. In our work, the thermal conductivity at room temperature and 700 K is originated from the experimental data (κ = 3.64 at room temperature and κ = 1.1 at 700 K)[20]. And then the two constantsandin the empirical formula κ =+/T[20]are calculated, thereby inferring κ = –0.805 + 1333.5/T. Finally, we can get the thermal conductivity for different temperature. Clearly, κ decreases as the temperature increases. Therefore, we can use it to obtain semi-quantitative information about the behavior of ZT versus doping concentra- tion and temperature, as is shown in Fig. 4d.

From Fig. 4d, we can see that when the tempera- ture rises, ZT rises tremendously until the tempe- rature reaches 900 K. The maximal ZT is 1.65, which is obtained at 900 K and n = 2´1020cm-3. The ZT value from the current work is significantly higher than that from our previous work on AgGaTe2systems (1.19)[5]. The higher ZT at 900 K for CuGaTe2is mainly contributed to the higher power factor and the lower thermal conductivity. Therefore, CuGaTe2is promising for high-temperature applica- tions. Furthermore, in the best condition, the Seebeck coefficient is about 80 μV/K, smaller than the experimental value[18]. Therefore, ZT of CuGaTe2may be further enhanced by reducing the Seebeck coefficient.

4 CONCLUSION

In this work, an attempt has been made to employ the first-principles calculation in combination with an empirical result to predict the dependence of TE properties of CuGaTe2on the doping concentration and temperature. The estimation of transport coefficients was performed using the Boltzmann transport equation with the assumption of a constant relaxation time. The results show that the optimal doping concentration is 2 × 1020cm-3in the tempe- rature range of 300～1000 K. Under the optimal doping concentration, the maximal ZT reaches 1.65 at 900 K, indicating that CuGaTe2is a very pro- mising thermoelectric material for the applications around 900 K.

(1) Tritt, T. M. Holey and unholey semiconductors.1999, 283, 804-805.

(2) Tritt, T. M. Subramanian, M.; Thermoelectric materials, phenomena, and applications: a bird's eye view.2006, 31, 188-198.

(3) Yim, W.; Fitzke, E.; Rosi, F. Thermoelectric properties of Bi2Te3-Sb2Te3-Sb2Se3pseudo-ternary alloys in the temperature range 77 to 300 K.1966, 1, 52-65.

(4) Charoenphakdee, A.; Kurosaki, K.; Muta, H.; Uno, M.; Yamanaka, S. Thermal conductivity of the ternary compounds: AgMTe2and AgM5Te8(M = Ga or In).2009, 50, 1603.

(5) Wu, W. T.; Wu, K. C.; Ma, Z. J.; Sa, R. J. Doping and temperature dependence of thermoelectric properties of AgGaTe2: First principles investigations.2012, 537, 62-64.

(6) Gudelli, V. K.; Kanchana, V.; Vaitheeswaran, G.; Svane, A.; Christensen, N. E. Thermoelectric properties of chalcopyrite type CuGaTe2and chalcostibite CuSbS2.2013, 114, 223707.

(7) Tang, X. F.; Xie, W. J.; Li, H.; Zhao, W. Y.; Zhang, Q. J.; Niino, M. Preparation and thermoelectric transport properties of high-performance p-type Bi2Te3with layered nanostructure.2007, 90, 012102-012102-3.

(8) Yusufu, A.; Kurosaki, K.; Kosuga, A.; Sugahara, T.; Ohishi, Y.; Muta, H.; Yamanaka, S. Thermoelectric properties of Ag1−xGaTe2with chalcopyrite structure.2011, 99, 061902.

(9) Kuhn, B.; Kaefer, W.; Fess, K.; Friemelt, K.; Turner, C.; Wendl, M.; Bucher, E. Thermoelectric properties of CuIn1-xGaxTe2single crystals.1997, 162, 661-671.

(10) Kresse, G.; Furthmüller, J. Efficient iterative schemes fortotal-energy calculations using a plane-wave basis set.1996, 54, 11169-11186.

(11) Blöchl, P. E. Projector augmented-wave method.1994, 50, 17953-17979.

(12) Kohn, W.; Sham, L. J. Self-consistent equations including exchange and correlation effects.1965, 140, A1133.

(13) Bjerg, L.; Madsen, G. K.; Iversen, B. B. Enhanced thermoelectric properties in zinc antimonides.. 2011, 23, 3907-3914.

(14) Ong, K. P.; Singh, D. J.; Wu, P. Analysis of the thermoelectric properties of n-type ZnO.2011, 83, 115110.

(15) Singh, D. J. Doping-dependent thermopower of PbTe from Boltzmann transport calculations.2010, 81, 195217.

(16) Madsen, G. K.; Singh, D. J.; Boltz, T. A code for calculating band-structure dependent quantities.2006, 175, 67-71.

(17) Zhou, J.; Bian, G. Q.; Zhu, Q. Y.; Zhang, Y.; Li, C. Y.; Dai, J. Solvothermal crystal growth of CuSbQ2(Q = S, Se) and the correlation between macroscopic morphology and microscopic structure.2009, 182, 259-264.

(18) Plirdpring, T.; Kurosaki, K.; Kosuga, A.; Day, T.; Firdosy, S.; Ravi, V.; Snyder, G. J.; Harnwunggmoung, A.; Sugahara, T.; Ohishi, Y. Chalcopyrite CuGaTe2: a high-efficiency bulk thermoelectric material.2012, 24, 3622-3626.

(19) Singh, D. J.; Du, M. H. Properties of alkaline-earth-filled skutterudite antimonides: A(Fe, Ni)4Sb12(A = Ca, Sr, and Ba).2010, 82, 075115.

(20) Li, Y. P.; Meng, Q. F.; Zhou, H.; Yang, J. F.; Cui, J. L. Thermoelectric properties of chalpyrite CuGaTe2.2013, 44. 552-558.

25 March 2014;

14 August 2014

the National Natural Science Foundation of China (Nos. 20973174 and 91122015) and the Scientific Research Foundation of Guangxi University (No. XBZ120059)

. E-mail: wkc@fjirsm.ac.cn