ABAQUS塑性损伤模型非线性分析在双向板试验中的应用研究

赵 勇， 沈小璞

（安徽建筑大学土木工程学院，安徽 合肥 230601）

0 引 言

工程结构中的力学问题，究其本质大都属于非线性的范畴，也就是所研究的此类结构体系的内部相应量与所作用在结构上的外在因素（包括力、位移、温度变化等）是非线性的关系，弹性理论中线性假设只是实际问题的一种简化，随着线性问题的基本理论和分析方法的日趋成熟、完善，加之弹性理论并不能满足实际工况的需要，故非线性问题的研究便成为学术界和工程应用方面的重点研究方向，而钢筋混凝土结构是目前最为广泛应用的一种结构材料，但是对钢筋混凝土结构进行准确的内力分析研究是很难的。随着电子计算机技术的飞速发展和有限元分析软件的出现，大大地促进了钢筋混凝土结构的非线性分析的研究，而大型通用有限元软件ABAQUS以精于复杂问题的求解和非线性分析见长，应用于钢筋混凝土结构非线性分析中能够达到较好的拟合效果。

本文将以ABAQUS软件所提供的三种混凝土材料的本构模型为基础，利用ABAQUS／Stand－ard中混凝土塑性损伤模型（Concrete Damaged Plasticity）来模拟，并且结合双向板试验，进行钢筋混凝土构件的非线性有限元模拟对比，验证在ABAQUS有限元分析中CDP模型应用到混凝土结构中可以较好的为解决实际工程提供分析参考。

1 混凝土本构模型

本模型选用清华大学过镇海教授提出混凝土的单轴拉压应力－应变曲线的模型。混凝土受压:

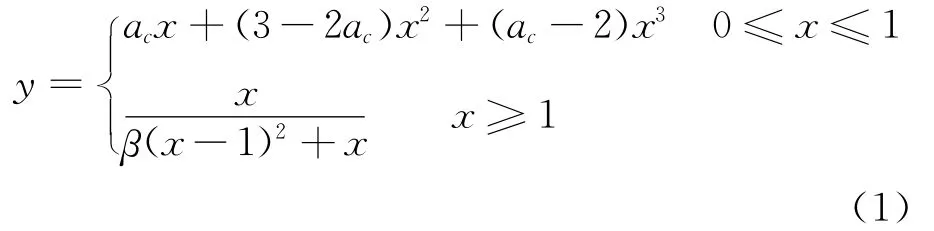
混凝土受拉:

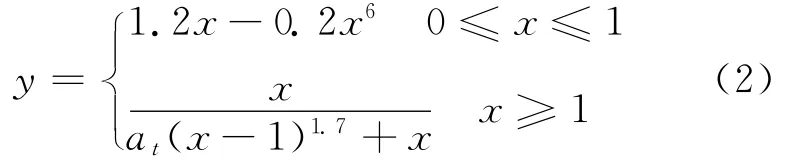
混凝土材料与结构的破坏失效是以材料内部裂纹萌生、扩展，并最终导致结构断裂破坏失去承载能力为特征的。固体力学的弹塑性与损伤耦合模型是目前常用的处理实际工程问题的理论工具［1－3］。

ABAQUS中塑性损伤模型是一个基于塑性的连续损伤模型［4］。模型假 设了混凝土材料的损伤机理有两种:一种是张开裂纹引起的损伤dt，另外一种是混凝土材料被压碎造成的损伤dc。损伤变量dt和dc的定义和演化律是通过各自相对应的一系列数值给出的。损伤变量的取值范围为［0，1］，分别表示初始损伤状态和最后的完全损伤状态。这样，由损伤因子来反映混凝土在受压、受拉时损伤引起的弹性刚度退化。

受压损伤因子（Damage Parameter）计算

混凝土受压时βc的取值范围为0．35－0．7。

受拉损伤因子（Damage Parameter）计算

受拉损伤因子的计算与受压损伤因子的计算方法基本相同:

混凝土受压时βt的取值范围为0．5－0．95。

本文采用C30混凝土，损伤图形见图1和图2。

图1 C30混凝土受压损伤－非弹性应变曲线

图2 C30混凝土受拉损伤－损伤应变曲线

2 钢筋混凝土双向板计算实例与试验

2．1 建模的简介

四边简支双向板尺寸3300mm×4400mm×120mm钢筋:短跨C 6＠150长跨C 6＠250见表1所示。混凝土:采用C30混凝土见表2所示。

表1 混凝土材料参数

表2 钢筋材料参数

混凝土选用C3D8R单元，钢筋选用T3D2单元模拟，然后采用Embedded技术将钢筋骨架嵌入到混凝土中，板下支座位置设置钢垫条以防止加载过程中的应力集中导致的不易收敛。钢筋本构采用双折线模 型钢筋实测强度值σyk＝478MPa，σsk＝645MPa．钢筋δ－εp见 图3。

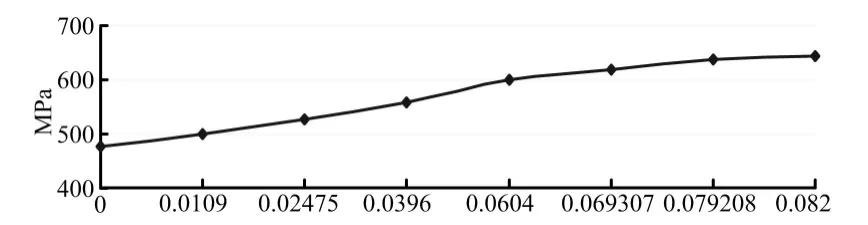
图3 钢筋δ－εp关系

2．2 理论计算与试验对比分析［5－12］

试验值与模拟值挠度对比见图4，荷载在6．69kN／m2（混凝土开裂）时，模拟值较试验值小0．4mm；而荷载7．37kN／m2至10．67kN／m2阶段，试验板底出现陆续出现一些裂缝，模拟值与试验值相差较大，荷载10．67kN／m2时模拟值比试验值小3．52mm；荷载11．01kN／m2时模拟显示板面大量出现损伤值大于0．5的区域，且挠度增加幅度大，试验荷载在10．67kN／m2后大量出现裂缝及开展，挠度也有突变，但是幅度远小于模拟值；试验板底跨中沿长跨方向出现第一条裂缝的荷载为6．69kN／m2，模拟模型中DAMAGET显示，在荷载为11．002kN／m2时，板底跨中位置沿长跨方向首先出现损伤大于0．5的值，见图5所示，故可以判断模拟板底已经出现裂缝，出现裂缝位置跟试验出现第一条裂缝位置基本一致。

图4 试验值与模拟值对比

图5 11．01kN／m2时板底塑性损伤

3 结论

混凝土塑性损伤模型（Concrete Damaged Plasticity），表达了混凝土非线性力学性能，不过只在塑性应变较小时比较准确，随着塑性变形增大，模拟值也渐渐偏离试验值较大，但是比较两者的变化趋势是基本一致的，工程设计中活荷载很少超过10．67kN／m2，故可以作为工程应用中的参考。

ABAQUS有限元软件具有较强的非线性计算能力，在钢筋混凝土结构全过程分析以及极限承载力计算等非线性研究方面有着广泛的应用［7］。本文通过一个试验例子与模拟结果进行对比，分析得出了ABAQUS损伤塑性模型CDP仅仅适用塑性应变较小的非线性阶段才比较准确，在塑性变形较大时，挠度变化趋势与试验基本一致，对于实际工程在满足楼板正常使用阶段的设计中，具有一定的参考价值；但是由于试验边界条件不可能达到完全的简支条件以及试验中一些不可预见的因素误差及模拟中材料模型与试验材料也存在差异，也会影响两者的对比分析结果。如何结合试验实测材料性能以及边界条件，使得模拟各项参数边界条件基本一致情况下进行对比分析，这些问题都有待于进一步研究解决。

1 谢和平．岩石混凝土损伤力学［M］．徐州:中国矿业大学出版社，1990．

2 Bazant Z P，Cedolin L．Stability of structures:elastic，inelastic，fracture and damage theories［M］．Oxford:Oxford University Press，1991．

3 余寿文，冯西桥．损伤力学［M］．北京:清华大学出版社，1997．

4 Lubliner J，Oller S，et al．A plastic damage model for concrete［J］．Int J Solids Struct，1989，25（3）:299－326．

5 过镇海．钢筋混凝土原理［M］．北京:清华大学出版社，2013．

6 沈新普．混凝土损伤理论及试验［M］．北京:科学出版社，2009．

7 石亦平．ABAQUS有限元分析实例详解［M］．北京:机械工业出版社，2012．

8 李兆霞．损伤力学及其应用［M］．北京:科学出版社，2002．

9 曹金凤．ABAQUS有限元分析常见问题解答［M］．北京:机械工业出版社，2012．

10 GB 50010－2010，混凝土结构设计规范［S］．

11 郭明．混凝土塑性损伤模型损伤因子研究及其应用［J］．土木工程与管理学报，2011，28（3）:128－132．

12 冯然．钢筋混凝土双向薄板的非线性有限元分析［J］．华中科技大学，2003．12，20（4）92－99．