基于大型有限元计算软件的结构模型内力优化设计

郝英奇， 王思启， 毛赫男

（安徽建筑大学 土木工程学院，合肥 230022）

0 引 言

有限元分析（FEA，Finite Element Analysis）是利用数学近似的方法对真实物理系统（几何和载荷工况）进行模拟的分析方法。其利用相对简单而又相互作用的单元元素，用有限数量的未知量去逼近无限未知量的真实系统［1－10］。

优化设计是一种寻求确定最优设计方案的技术，最优设计是指一种方案可以满足所有的设计要求，而且所需的支出（如重量、面积、体积、应力、费用等）最小［7－10］。

本文针对第五届全国大学生结构设计大赛的赛题《带屋顶水箱多层竹质框架结构模型的抗震结构设计》，结合本校及其他高校的参赛作品，利用大型有限元软件ANSYS进行相关的内力分析与设计优化［3］。通过ANSYS提供的零阶方法中的子问题近似法与多个求解模型对比，从而获取最优解。

这城市的街道比刚睡醒的头发还乱，路况比孟尝君的食客还杂，因此公车的行进像多数人的人生一样，通常很坎坷。

1 建模求解

1．1 模型几何尺寸

本文利用ANSYS建模的框架结构如图1所示:总高1m；层高25cm；底板22cm×22cm；顶面为15cm×15cm。

作为上市公司，在融资方式、渠道方面相对较多，企业应做好资金运用规划，使资金能得到有效合理的使用，将暂时闲置的资金及固定资产等投入到生产当中，提高企业的盈利能力。同时优化各部门分配配置，争取使用最小的资金消耗实现最大的资金回收。通过生产环节程序化，通畅采购、销售渠道等方式来减少企业成本，使企业的财务竞争力逐步增强，增强核心竞争力。

图1 基本模型

1．2 荷载计算及构件截面尺寸

（13）分别定义:设计变量 A、B、C、D、E、F、G，状态变量单元最大应力SEQV、目标函数VOLU的范围及条件

出港数据与进港数据计算过程类似。首先将厦门港出港船舶数据导进MATLAB软件，在MATLAB软件中进行计算，形成一个3 188×1的矩阵，得出以下结果。

该模型主体设计为框架结构，框架构件为柱和梁，其中柱承受着上部结构的绝大部分荷载，因此柱的结构选型很重要。根据静力分析来选择截面类型，截面类型有箱型截面、L形截面及圆形截面三种，本模型的设计变量为截面的各尺寸，状态变量为最大压应力，目标函数为体积。三种截面的设计变量初始值及变化区间如表1（单位:mm）所示。

表1 柱截面设计变量及初始值

梁和斜撑的截面尺寸取值如表2（单位:mm）所示。

表2 梁与斜撑截面变量及初始值

1．3 材料性质定义

ANSYS建模过程中梁取BEAM188单元，板取SHELL63单元，材料弹性模量EI＝1×104MPa，泊松比v＝0．3。由于竹皮为各向异性材料，顺纹抗拉能力和抗压能力均较强，而双层0．2mm厚的竹皮经胶水处理后的顺纹抗压强度约为30MPa，抗拉强度约为80MPa，均有所增强。考虑压杆屈曲问题、制作工艺误差和动力因素等问题，对最大压应力进行折减，取15MPa。强度以第四强度理论下的等强度应力SEQV控制，最小质量用总体积控制。为减小板的应力集中的影响，将板厚设置成3．5毫米，求得的最终体积减去板的体积后乘以密度为模型质量（竹皮的密度取为1020kg／m3）。

1．4 建模计算

以箱型截面建模为例，步骤如下:

（16）提取结果

调查显示：“对社会贡献”、“高尚人格”、“干一番事业”是胜利学院大学生的主要价值趋向。能否更好地提高自身素质、促进自身发展成为主导大学生价值取向的重要内容。说明当前大学生价值取向的主流呈现出积极、健康、向上的良好发展态势。

（2）定义材料单元为BEAM188、SHELL63

只有认识到著作权为仅赋予著作权人许可或禁止他人以法律规定的方式利用其作品，才是对著作权正确的理解。如何理解《著作权法》第10条要具体规定著作权人的16项具体权利，而不是像物权那样概括规定物权人的权利？这正是一种对著作权人垄断其作品的限制，使其只能限制他人以有限的特定方式利用其作品，而这以外的其他利用行为，如对作品的阅读、背诵，乃是公众的自由，以体现“法无禁止即自由”，保证公众对作品的自由接触权，进而促进作品的流通，最终达到知识产权法促进知识和信息的广泛传播，促进经济的发展和科技、文化进步⑲ 冯晓青著：《知识产权法利益平衡理论》，中国政法大学出版社2006年版，第82页。的最终目的。

（3）定义实体参数TK＝3．5mm

（4）定义材料属性值EI＝1e4MPa、v＝0．3

缺钼发生原因：强酸性红壤柑橘园，钼被土壤固定，有效钼含量低。其次，土壤中磷不足时，钼的吸收率降低，硫酸盐肥料施用过多，钼的吸收被抑制，容易发生缺钼。

在系统内各电站上位机服务器与集控中心通信服务器之间的通信采用TCP/IP协议通信，各电站的通信服务器采用双网口（不在同一网段）。

箱型截面:根据SEQV与VOLU的关系曲线可见，在VOLU取到617．5附近的值时，SEQV取得较小值15．9MPa，此时斜撑截面各取值为最大，梁的截面宽接近最小值，且G曲线的上升造成最大应力快速减小，故主要受力控制截面在斜撑上。

（7）定义截面尺寸类型

（8）网格划分及定义截面

（9）施加约束和荷载

（10）求解，获取结果

（11）提取参数，对模型总体积求和，获取最大压应力

（12）建立优化文件

根据建立的模型，将铁块转化为均布荷载作用在楼面上，水箱作为阻尼减震器。在设计优化过程中将其质量转化为满载作用在顶层楼面上。杆件下部内力达到最大值，为减少应力集中现象，将铁块荷均匀的布置在下三层楼面上。荷载取值为:水箱荷载P0＝1．78KPa，第一到三层楼面荷载P1＝2．9KPa。

（14）设定输出、运行次数

（15）运行求解

（5）建立几何模型（点、线、面）

（1）定义工作文件名，取ANSYS OPT1

其中第（10）步求解结果云力图细节如图2所示。

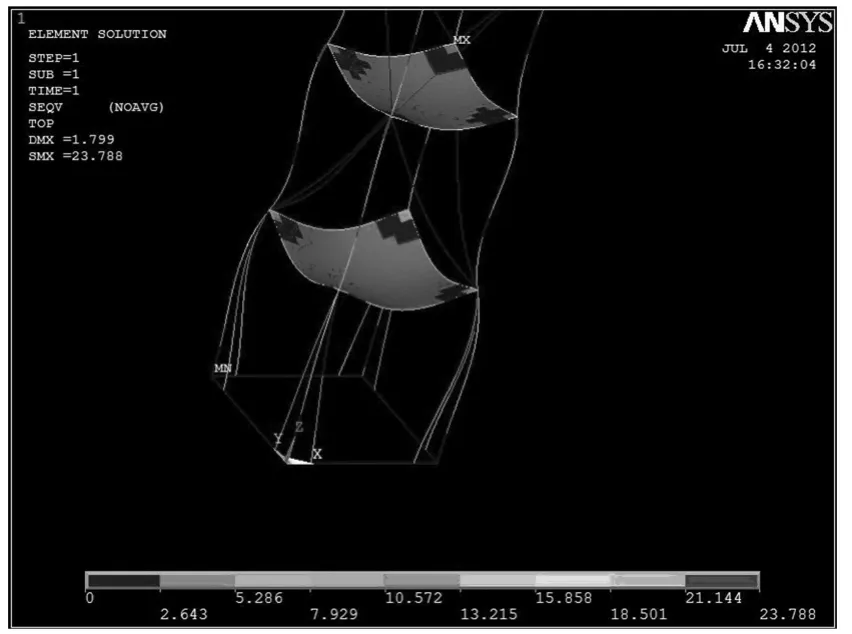
图2 箱型截面结构内力云图

1．5 结果提取

根据与上述相同的方法对圆截面柱和角钢截面建模优化分析后结果分别如图3和图4所示。

图3 角钢截面各设计变量与体积迭代的关系

图4 圆形截面各设计变量与体积迭代的关系

2 结果分析

2．1 内力优化效率

板的厚度实际值为0．2mm，由于未进行优化，在设计中为减小板对设计的影响，取作3．5mm，计算优化效率时应减去其产生的体积Vb＝415．1cm3。优化 效率计算 公式H＝ （P1－P2）／P1＋（V1－V2）／（V1－Vb），优化效率如表2所示。

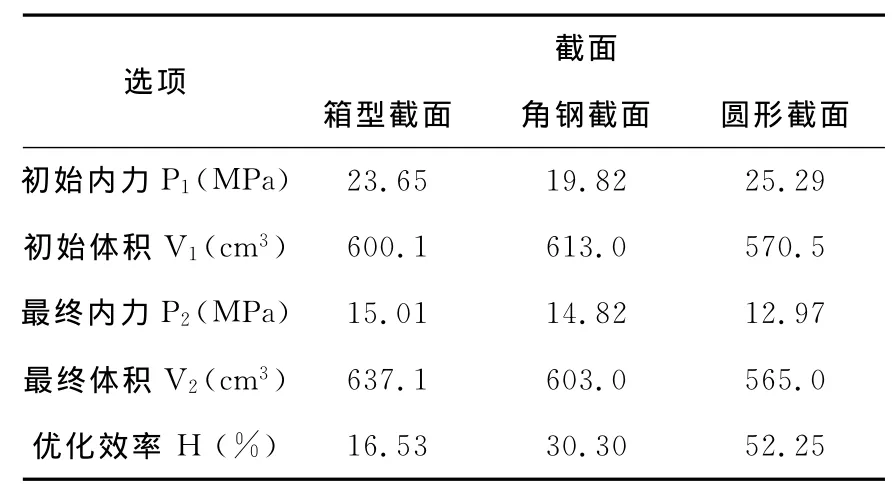
表2 优化设计效率表

2．2 变量结果分析

（6）定义参变量A、B、C及其初始值

汤翠被这个消息撩拨得很兴奋，开门的动静闹得比平时大。侯大同听到大门响，身子从无花果树后面露出来。汤翠走过去，妩媚地笑了一下。侯大同猜，老婆肯定又有什么高兴事了。

角钢截面:由设计变量与体积迭代关系图得知，最佳设计值在VOLU＝575．0－580．0之间，其应力值比设计值15MPa稍大，但质量较最佳设计值结果减轻许多。

圆形截面:根据曲线图，两个最大应力的较小值处分别出现在E值和G值最大时，故最大应力单元点是在斜撑和梁上交替出现的。且梁的应力由E值控制，说明梁上最大应力是弯矩造成的。

3 结 论

经过建模分析，得出如下结论:

线上：从之前的线上统计情况来看，参加线上问卷调查的人有60.49%的人参观过一两次南京城墙，有6.17%的人经常前往参观，24.69%的人虽然没去过但是愿意前往参观，但也有8.64%的人对此没有兴趣。数据说明，大多数人对于南京城墙还是有一定的了解和兴趣的，但是也有一小部分人对此比较淡漠。

（1）最终差异化优化结果体积约为75．7cm3，得到的模型质量为78g，与此次比赛特等奖西南交通大学的制作模型结果76g非常接近。

要在最严格水资源管理制度试点工作带动下，全面推进最严格水资源管理各项工作，确保各项制度有措施、能落地。一是按照“节水优先、空间均衡、系统治理、两手发力”的治水思路，以水定需，量水而行，因水制宜，严格水资源论证、取水许可管理和水资源有偿使用制度。二是把节约用水贯穿于经济社会发展和群众生活全过程，优化用水结构，切实转变用水方式，全面实行计划用水管理，加快推进节水技术改造。三是全面落实 《全国重要江河湖泊水功能区划》，从严核定水域纳污容量，切实加强水污染防控，加强饮用水水源保护，推进水生态文明建设。四是按照最严格水资源管理制度考核工作要求，积极有序开展辖区内考核工作，切实落实水资源管理责任制。

（2）根据总体受力图，下部斜撑平均内力较大，而上部斜撑平均内力很小，可以考虑取消上部斜杆，或用单层竹皮做为斜拉，且地梁可以舍去以减小质量。在下部结点处有应力集中现象，应作适当处理。

（3）实际模型选型中应选择圆形截面，这也与西南交通大学独家选用圆截面而技压群雄的事实相符，其原因在于箱型截面较费材料，且内力较大，实际制作过程中最优值的理论范围较小，不易控制。而角钢截面中内力值随设计变量起伏较大，亦不易控制。取圆形截面时，在E和G值达到最大值之前，内力与变量的关系较为平缓。

（4）模型的设计优化效率可达15%－55%，由于上部杆件与下部杆件受力差异较大，若对各层杆件差异化进行优化设计，效率将进一步高；若将有限元结构设计优化应用于实际工程当中，必然会有很好的效果。

1 涂振飞．ANSYS有限元分析工程应用实例教程［M］．北京:中国建筑工业出版社，2010:292－299．

2 林少玲，陈铭年，徐健全，等．ANSYS结构分析单元的分类［A］．福建农林大学，2004:1－4．

3 高 诚，陆 帅，李雪蕾．第五届全国大学生结构模型设计书［Z］．东南大学，2011:6－8．

4 施二铁，杨国峰．ANSYS在结构设计中的作用［A］．华南理工大学，2012:1－4．

5 Design Optimization，Release 10．0Documentation for ANSYS

6 商跃进．有限元原理与ANSYS应用指南．北京:清华大学出版社，2005．

7 MARCEL IN J L．Evolutionary Optimization of Mechanical Structures:Towards an Integrated Optimization［J］．Engineering with Computers，1999，15:326－333．

8 NIKOLAOS D．Lagaros，Manolis Papadrakakis，George Kokossalakis，Structural optimization using evolutionary algorithms ［J］．Computers and Structures，2002，80:571－589．

9 陈建军，车建文．结构动力优化设计述评与展望［J］．力学进展，2001，31（2）:181－192．

10 杨荣柏．机械结构分析的有限元法［M］．武汉:华中理工大学出版社，1989．