城市道路中黄灯期间的驾驶行为研究

马小龙 孙小端 贺玉龙 陈亦新

（北京工业大学城市交通学院 北京 100144）

0 引言

黄灯启亮时，在距离停车线的一定范围内，由于驾驶员、车辆速度等因素的不同，部分驾驶员选择通过，部分选择停车。这种由于驾驶员本身决策的不同，客观存在于停车线上游一定范围内的区域，被称为第2种黄灯困境区［1］，也称为犹豫区。理解黄灯期间的驾驶行为对于黄灯期间的安全保障、以及黄灯信号时长的设置均具有重要意义。

1974年P.S.Parsonson等人［1］首次提出犹豫区概念，文献［2］对困境区与犹豫区进行了详细的解释，犹豫区的定义为：与停车线距离为S1时，90%的车辆选择通过，与停车线距离为S2时，10%的车辆选择通过，则S1～S2这段道路空间被定义为犹豫区，见图1。笔者重点研究车辆在黄灯期间犹豫区的驾驶行为。

1 文献综述

国内外研究中获取数据的方法主要有视频观测［3－4］、模拟仿真［5］、实地试验［6］这3种方法。笔者采用视频拍摄的方法获取数据，在道路交叉口附近选择制高点进行拍摄，之后利用SIMI软件，提取不同时间的车辆位置信息，获取其行驶速度，经过校正之后，精度可达95%以上。

龙科军等［7］利用二元Logistic回归模型描述驾驶员的闯黄灯行为，主要考虑因素为黄灯启亮时车辆的速度，与停车线的距离。辛秀颖等［8］基于经济学中风险决策理论，分析驾驶员在交叉口的闯黄灯行为决策过程和主要影响因素。P.Papaioannou［9］考虑了车辆的运行速度，与停车线距离，通过研究确认车辆的闯黄灯行为与驾驶员的年龄有一定的关系，并建立了与年龄有关的闯黄灯行为模型。J.K.Caird等［5］利用汽车驾驶模拟器（模拟速度为70km／h）研究了年轻人与老年人在黄灯启亮时的反应时间和闯黄灯行为，运用Logistic回归分析的方法，建立了闯黄灯的行为模型，最后将到达停车线的时间作为惟一变量。也有学者利用分类决策树［10］的方法，得出车辆行驶速度、与停车线的距离，以及在交通流中的位置是影响驾驶员闯黄灯的主要因素的结论。

总体来说，关于黄灯期间的驾驶行为，国外的主要研究对象是公路交叉口，而中国主要是城市道路。

2 基本情况介绍

2.1 交叉口介绍

本次试验主要选取了城市道路中2种常见的信号控制交叉口：十字形交叉口与路段人行横道，无倒计时，绿灯将要结束时无绿闪。

十字形交叉口东西向为双向6车道，南北向为双向4车道，主要分析由东向西的车辆闯黄灯行为，宽度为50 m，有闯红灯监控摄像头。且该交叉口与上游交叉口距离为400 m，由于与上游交叉口距离较远，故上游交叉口对车辆行驶速度影响较小。

对于路段人行横道，其所在路段由4块板组成，主路为双向6车道，中间有铁栅栏隔离，行人过街斑马线宽度为8m。主路有闯红灯监控摄像头，辅路无闯红灯监控，为了保持与十字形交叉口研究的一致性，仅研究主路的闯黄灯行为。

2.2 数据介绍

主要考虑正常交通情况下的闯黄灯行为，交通拥堵时期的闯黄灯行为暂不考虑。在非拥堵情况下，由于黄灯位于绿灯结束之后，所以排队车辆基本放行结束，尾部车辆一般处于正常行驶状态。研究对象为小汽车。在实际观测中发现部分车辆在绿灯将要结束，黄灯还未启亮时，主动降低运行速度，由于该类型车辆运行速度较低，不存在闯黄灯行为，故将黄灯启亮时运行速度小于20km／h的车辆剔除。数据统计见表1。

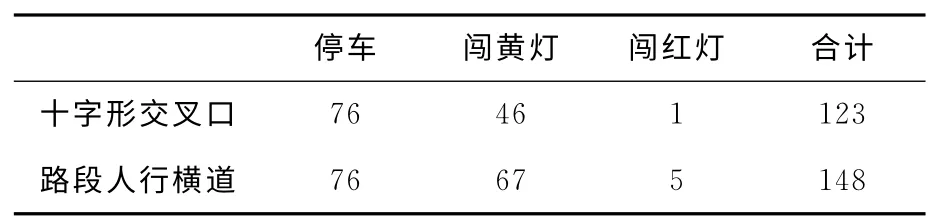
表1 数据统计结果Tab.1 The statistical results 辆

为方便研究引入闯黄灯率的概念：在距离交叉口停车线100m 的范围内，黄灯期间通过的车辆数，与总车辆数的比值为闯黄灯率，这里总的车辆数是指黄灯启亮这一时刻落在停车线上游100 m 范围内的车辆，不包括后来到达的车辆。其计算式为

式中：μ为闯黄灯率；n为黄灯期间通过的车辆数；N为黄灯启亮这一时刻，在距离停车线100m范围内的车辆总数。

通过计算可得，路段人行横道黄灯期间选择通过的比例为46.9%，十字交叉口为37.7%。

3 车辆运行数据分析

3.1 十字形交叉口

图2为十字形交叉口车辆闯黄灯行为与到停车线距离的关系图，可以看出与停车线距离约为15m 时，90%的车辆选择通过，距离约为62 m时，有10%的车辆选择通过。当车辆运行速度为20～70km／h时，十字形交叉口的犹豫区的空间范围是停车线上游15～62m。

时间距离计算方法如下。

图3为十字形交叉口闯黄灯行为与车辆到停车线时间距离的关系，当到停车线的时间距离小于1.8s时，约90%的车辆选择通过，当距离停车线的时间距离为5.2s时，约10%的车辆选择通过。当到停车线的时间距离为3s以内时，选择通过的比例高于停车的比例；大于3s时，选择停车的比例高于通过的比例。到停车线的时间距离在3.5s内时，随着时间的增大，闯黄灯的车辆急速减少，到6.5s之外时，闯黄灯的车辆几乎为零。

图3 闯黄灯行为与时间距离的关系图Fig.3 The relationship between driver behavior and time distance

3.2 路段人行横道

图4为路段人行横道车辆闯黄灯行为与到停车线距离的关系图，车辆运行速度的区间为20～70km／h。由图4可见，到停车线距离约为25m时，90%的车辆选择通过，当距离约为68 m 时，仅有10%的车辆选择通过。当车辆运行速度为20～70km／h时，路段人行横道犹豫区的空间范围是停车线上游25～68 m。到停车线距离小于40m 时，通过百分比大于停车百分比，大于40m时结果相反。在35～45 m 的空间范围内，闯黄灯车辆百分比下降速度最快。

图4 闯黄灯行为与空间距离的关系Fig.4 The relationship between driver behavior and spatial distance

图5为路段人行横道车辆闯黄灯行为与到停车线时间距离的关系图，到停车线的时间距离越小，闯黄灯可能性越大。与十字形交叉口规律类似。到停车线的时间距离为2s时，约90%车辆选择通过，时间距离约为4.9s时，仅有10%选择通过。表2 为2 种类型交叉口的犹豫区对比分析。

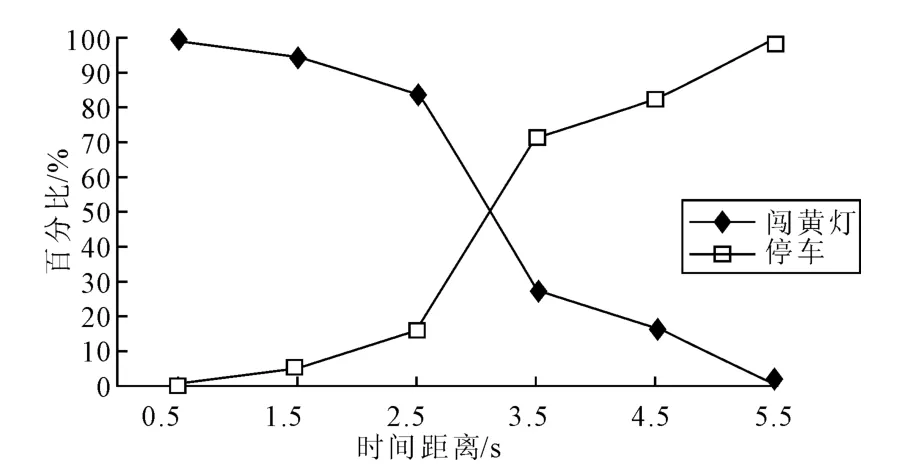
图5 闯黄灯行为与时间距离的关系图Fig.5 The relationship between driver behavior and time distance

表2 犹豫区对比表（20～70km／h）Tab.2 A comparison of dilemma zones（20～70km／h）

路段人行横道犹豫区与十字形交叉口相比，空间位置较为靠后，但是两者时间区间相差较小。

4 闯黄灯行为模型建立

利用速度、距离2 个基本变量建立二元Logistic模型，模型如下。

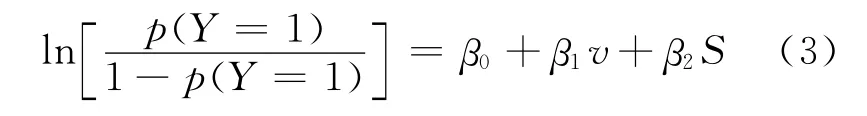
式中：p（Y＝1）为车辆闯黄灯的概率；β0 为常数；β1，β2 为自变量系数；v为黄灯启亮时车辆的运行速度，km／h；S为黄灯启亮时车辆到停车线的距离，m。

分别建立十字形交叉口与路段人行横道的闯黄灯行为模型，Spss分析结果见表3。

由表3中可见，速度项的系数为正，距离项的系数为负，速度越大越容易闯黄灯，距离越大，闯黄灯的可能性越小，模型结果与实际情况相符合。

通过分析发现，2 个交叉口的空间犹豫区不同，但时间犹豫区较为接近。因此，利用时间距离这个因素建立闯黄灯行为模型，该模型包含了十字交叉口与路段人行横道。利用Spss软件分析结果见表3。

时间距离的系数为负，时间距离越大，闯黄灯的可能性越小，与实际情况相符合。上述模型中Sig＜0.05，在5%的置信水平下通过了有效性检验。图6为模型的最终标定结果，图中2条S形曲线为最终拟合的模型结果，分别为时间距离与停车、闯黄灯概率的关系曲线，2条竖直平行虚线为时间犹豫区的分布范围。

表3 模型标定结果Tab.3 The result of model

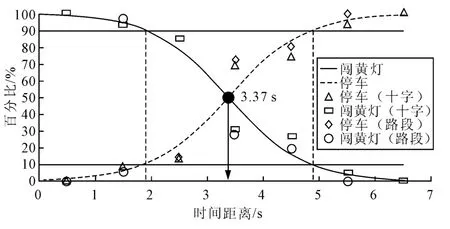
图6 模型标定结果Fig.6 The result of the model calibration

由模型计算可得，当时间距离为1.89s时，停车的概率为10%，当时间距离为4.86s时，停车的概率为90%。时间距离小于3.37s时，闯黄灯概率高于停车概率，时间距离大于3.37s时，结果相反。从3～4s的时间距离区间内闯黄灯概率降低值最大，总体来说闯黄灯概率随着时间距离的增加逐渐下降，下降速度呈现出“慢－快－慢”的趋势。

5 结束语

利用实际观测数据，分别分析了城市道路中的十字形交叉口与路段人行横道的闯黄灯行为，并引入了闯黄灯率的概念。十字形交叉口的空间犹豫区为15～62m，路段人行横道的空间犹豫区为25～68m，路段人行横道的空间犹豫区比十字交叉口靠后，但两者时间犹豫区较为接近。之后利用速度、距离2个因素分别建立十字型交叉口与路段人行横道的二元Logistic闯黄灯行为模型，最后利用时间距离这1个因素建立闯黄灯行为模型，并且模型的拟合度较好。

由于仅对城市道路中2种常见交叉口进行了观测分析，所以数据样本量还需要进一步增加。不同车型的闯黄灯行为，如铰接公交车与普通客车，在不同时间段，如白天与夜间的闯黄灯行为也需要进一步研究。

［1］Parsonson P S，Roseveare R W，Thomas Jr J R.Smallarea detection at intersection.pproaches［R］.Washington，DC：Institute of Traffic Engineers，1974.

［2］Urbanik T，Koonce P.The dilemma with dilemma zones［C］∥ITE District 6 Annual Meeting，Portland：Ore.，2007，6.

［3］Gates T J，Noyce D A，Laracuente L.Analysis of dilemma zone driver behavior at signalized intersections［C］∥Transportation Research Board 86th Annual Meeting，Washington，DC.：TRB，2007.

［4］Hurwitz D S，Wang H，KnodlerJr M A，et al.Fuzzy sets to describe driver behavior in the dilemma zone of high－speed signalized intersections［J］.Transportation research part F：traffic psychology and behaviour，2012，15（2）：132－143.

［5］Caird J K，Chisholm S L，Edwards C J，et al.The effect of yellow light onset time on older and younger drivers’perception response time（PRT）and intersection behavior［J］.Transportation research part F：traffic psychology and behaviour，2007，10（5）：383－396.

［6］Rakha H，El－Shawarby I，Setti J R.Characterizing driver behavior on signalized intersection approaches at the onset of a yellow－phase trigger［J］.Intelligent Transportation Systems，IEEE Transactions on，2007，8（4）：630－640.

［7］龙科军，何林儒，韩 立.黄灯期间信号交叉口的驾驶员行为［J］.系统工程，2010，28（12）：117－120.Long Kejun，He Linru，Han Li.Driver behavior at signalized intersection during yellow interval［J］.Systems Engineering，2010，28（12）：117－120.（in Chinese）.

［8］辛秀颖，马寿峰，贾 宁.“闯黄灯”决策的影响因素分析：基于意向调查方法［J］.交通信息与安全，2013，31（3）：15－27.Xin Xiuying，Ma Shoufeng，Jia Ning.Incentive of yellow－light－running from economic perspective based on stated preference（SP）Survey［J］.Journal of Transport Information and Safety，2013，31（3）：15－27.（in Chinese）.

［9］Panagiotis P.Driver behaviour，dilemma zo0ne and safety effects at urban signalised intersections in Greece［J］.Accident Analysis and Prevention，2007，39（1）：147－158.

［10］Elmitiny N，Yan X，Radwan E，et al.Classification analysis of driver＇s stop／go decision and redlight running violation［J］.Accident Analysis ＆Prevention，2010，42（1）：101－111.