改进的灰色预测GM(1,1)模型的MATLAB实现
杨 旭
(郑州大学水利与环境学院,河南 郑州 450001)
0 引言
灰色系统理论[1]是由我国学者邓聚龙教授于1982 年在国际上首先提出来的,用于研究少数据、贫信息的不确定性问题的理论方法。该理论的主要内容之一就是以GM(1,1)模型为核心的预测模型体系。该模型在工业、农业、商业等经济领域以及环境、社会等领域中都有广泛应用。然而在使用GM(1,1)模型进行预测的过程中,也会出现预测模型精度较低的情况。许多学者提出了改进预测模型精度的方法[2-3]。其中,杨华龙[4]等学者在分析了以往学者的改进方法后认为虽然以往学者提出的模型改进方法对模型精度的提高有所帮助,但模型预测公式本身存在的缺陷并未得到有效的改进。因此在分析了GM(1,1)模型预测公式的形成过程后,提出并使用自动寻优定权对背景值进行了选择,使用最小二乘法原理对GM(1,1)模型的初始值进行了改进。且通过实例结果表明,提出的改进方法是有效和完善的,对GM(1,1)模型的预测精度也有较大的提高。
MATLAB 是美国MathWorks 公司出品的科学计算软件,具有强大的科学计算功能和出色的图形处理功能,被广泛地应用于教学和科研之中,是人们进行科学计算等工作的强大有力的工具。
鉴于此,本文使用MATLAB 语言编写算法,实现改进的灰色预测GM(1,1)模型的程序化,有利于相关学者在实际工作中方便使用改进的GM(1,1)模型,进行便捷而又科学地开展预测等研究工作。
1 改进的灰色预测GM(1,1)模型
建立传统GM(1,1)模型的原理及具体步骤参见文献[1]。
这里直接给出传统GM(1,1)模型的时间响应公式为:
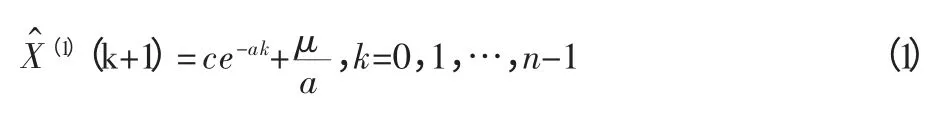

代入式(1)得

对式(3)作累减还原便得原始数列的预测公式

在文献[4]中,杨华龙等学者给出了模型改进流程图(见图1),并代表性地详细介绍了背景值的权重系数μ=0 时的改进过程。这里只给出最终结果。
令C=c·(1-ea),将C 分别代入式(1)和式(4)中可得
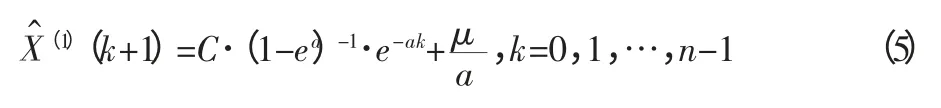
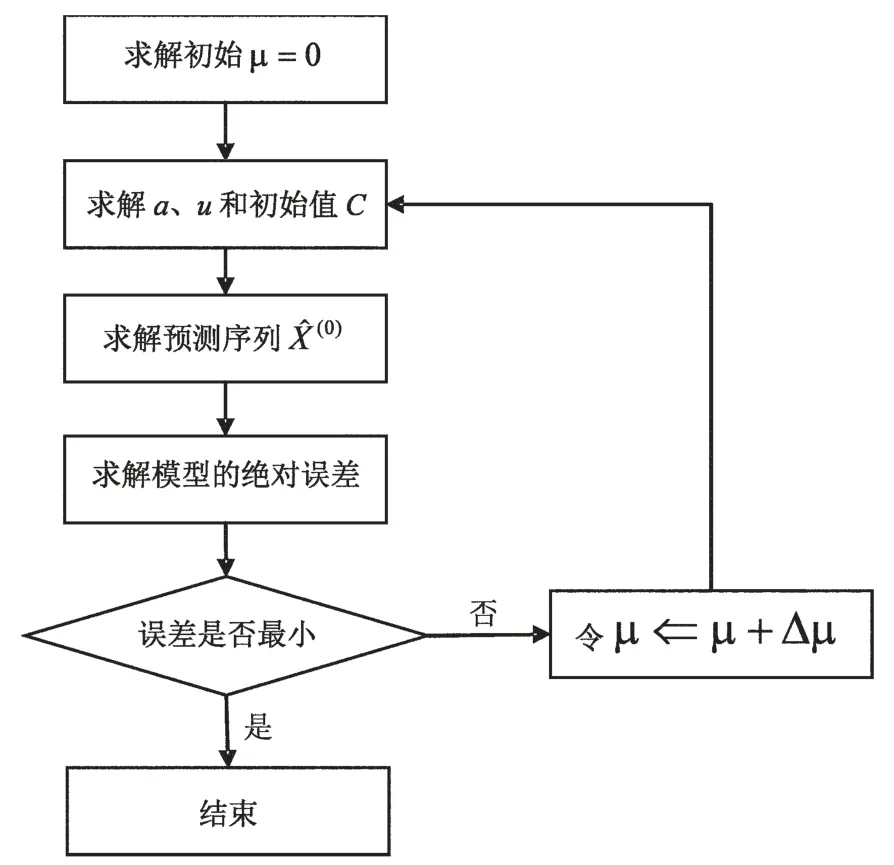
图1 模型改进流程图
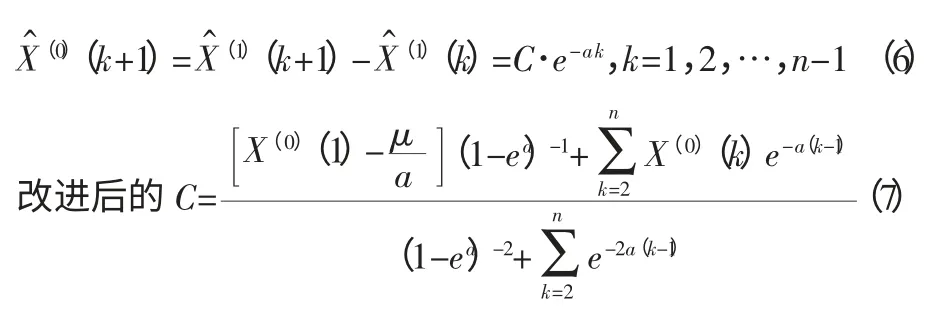
代入式(6)即可得改进模型下背景值权重系数μ=0 时的原始数列预测值。接下来便利用原先求解过程中的计算该权重下的离差平方和。然后在此基础上增加一个大于零的微小量Δ μ,即μ⇐μ+Δ μ,重复上述过程直至μ=1。在此过程中,可以比较不同权重下预测值与实际值的离差平方和,选取离差平方和最小时的权重系数作为最佳权重,建立模型进行预测。
2 MATLAB 算法实现


3 结语
本文给出了改进的灰色预测GM(1,1)模型的MATLAB 算法程序,通过计算机快速的运算就可以得到丰富的数据,从中选取符合要求的目标数据;通过MATLAB 绘制的关系图亦可直观了解相关参数的关系走势。MATLAB 强大的科学计算功能与出色的图形处理功能为我们的计算工作提供了极大的便利。本文给出的算法程序对解决相似问题具有一定程度上的借鉴意义。
[1]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].5版.北京:科学出版社,2010.
[2]李云贵,李清富,赵国藩.灰色GM(1,1)预测模型的改进[J].系统工程,1992(6):27-31.
[3]樊新海,苗卿敏,王华民.灰色预测GM(1,1)模型及其改进与应用[J].装甲兵工程学院学报,2003(2):21-23.
[4]杨华龙,刘金霞,郑斌.灰色预测GM(1,1)模型的改进及应用[J].数学的实践与认识,2011(23):39-46.

