基于ARIMA-BP神经网络的组合模型在地基沉降预测中的应用研究
邹进贵,肖扬宣,张士勇
(1.武汉大学测绘学院,湖北 武汉430079;2.精密工程与工业测量国家测绘地理信息局重点实验室,湖北武汉430079)
一、引 言
工程设计、施工、竣工后的沉降监测与控制极为重要,如果对软土地基沉降的预测不准确,则可能导致建筑物的功能失效,甚至造成坍塌等严重事故。现阶段,大多数组合预测方法是通过权系数把若干种不同单一方法加权组合进行预测,能够在一定程度上提高预测精度。本文对基于ARIMA-BP神经网络的3种组合预测模型进行了研究,并根据某地基沉降数据进行了预测研究,对3种方法的预测结果与精度进行了分析。
二、单一预测模型
1.时间序列分析法
时间序列分析法是利用数据的自相关性建立相对最优的模型来分析客观现象的动态特征[1]。时间序列分析的目的是认识产生观测序列的随机机制,再基于序列历史数据,对序列未来的可能取值给出预测或预报[2]。其主要模型为ARIMA(auto regressive integrated moving average)模型。
如果一个时间序列 Yt{ }的d次差分Wt=ΔdYt是一个平稳的ARMA过程,则称 Yt{}为自回归滑动平均求和模型,记为ARIMA(p,d,q),其中d为差分次数。
ARIMA模型的通用表达式为
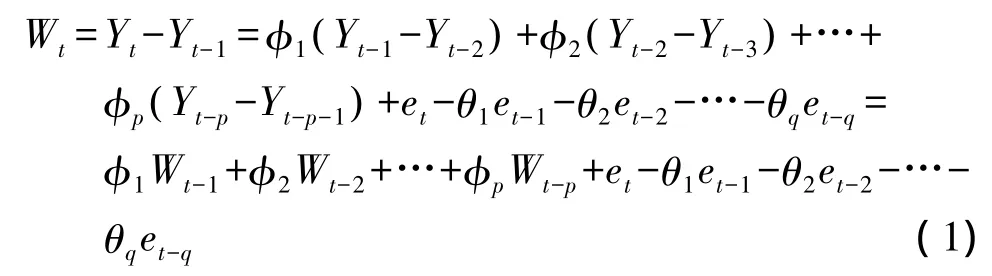
式中,φ1,φ2,…,φp是自回归系数;p是自回归阶次,θ1,θ2,…,θq是滑动平均系数;q是滑动平均阶次;et是白噪声序列,该模型通常表示为ARIMA(p,d,q),其中d为差分阶次。
ARIMA模型的建模及预测过程分为以下几个步骤。
1)模型识别:检验序列的平稳性,对非平稳序列进行差分处理,再对模型定阶。
2)参数估计:对模型φ,θ等系数进行估计。通常采用最小二乘估计、极大似然估计等。
3)模型诊断:进行模型适用性检验,分析拟合模型的残差。
4)预测:用所得时间序列模型进行预测。
2.BP神经网络法
BP神经网络是人工神经网络中使用最多的一种网络。BP(back-propagation)是前馈的意思,该网络由3层组成:输入层、隐含层和输出层[3],如图1所示。
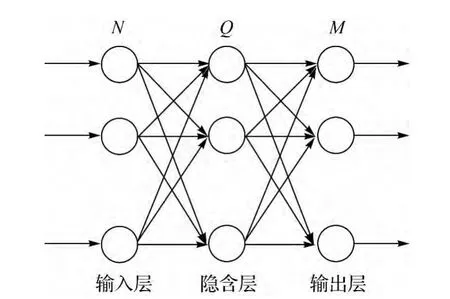
图1 BP神经网络结构
3层的节点个数分别记为:N、Q、M。BP神经网络神经元模型[4],如图2所示。

图2 神经元模型
其中,xj(j=1,2,…,N)为神经元 j的输入信息;wij则为网络的连接权重;ui是输入信号和连接权值内积的结果,是神经元i的输入信号;经过阈值θi的调整,作为激活函数的自变量,得到神经元的输出yi。神经元的激活函数常采用Sigmoid函数

BP神经网络的学习过程为信号的正向传播和学习误差项的反响传播。信号正向传播过程为:信号从输入层进入,通过权值调整进入隐含层。输入层和隐含层阈值组合形成隐含层的输入,再经过激活函数的输出。从隐含层到输出层的过程类似。
学习误差项反向传播:网络根据学习误差的大小,重新调整网络的权值和阈值。权值重新调整之后,再进行训练样本的学习。如果训练误差仍没有达到精度要求,则继续反向传播,直到训练误差达到要求。
三、组合预测模型
1.误差平方和最小组合模型
假设 xt{}为有N个数据的序列[5],现有m种预测方法,第i种预测方法在t时刻的预测值为xit,第i种预测方法所占权重为li,则序列 xt{}在t时刻的预测值^xt满足式(3)

这是把权系数的求解转化为求解一个最优化问题,使组合模型的误差平方和达到最小。
设序列 xt{ }在t时刻的误差为eit,则可得该模型以下的最优化问题

2.调和平均组合模型
假设 xt{}为有N个数据的序列,现有m种单项预测方法,第i种预测方法在t时刻的预测值为xit,第i种预测方法所占权重为li。设组合模型在t时刻的预测值为xt,根据加权调和平均数计算公式[6]
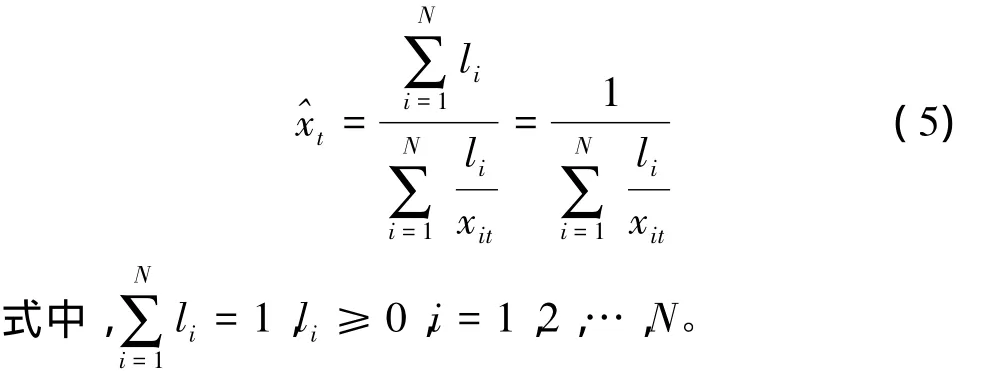
为便于对该模型进行组合权系数的估计,稍微转换式(5)后引入误差项

可得该模型以下的最优化问题

3.对序列线性和非线性规律单独描述的组合模型
由于软土地基特殊的性质[7],其沉降规律受到多种因素制约,使沉降过程既包含线性规律又包含非线性规律。历史数据中既有线性趋势,又有非线性趋势[8],单独使用某一种模型无法准确刻画其规律。需要使组合模型不仅可以通过ARIMA模型有效捕抓到序列间的相关性,还能通过BP人工神经网络模型来弥补ARIMA模型所无法刻画的序列的非线性关系。
该络组合模型进行预测有以下几个步骤:
1)使用时间序列分析方法对序列建立合适的ARIMA模型,并根据ARIMA模型计算拟合误差序列并对样本进行预测。
2)由1)中得到的拟合误差序列,使用BP神经网络建模并预测ARIMA模型拟合误差。
3)用2)中得到的拟合误差的预测值对1)中得到的预测值进行修正,得到最终组合模型的预测值。
四、工程应用
某工程地基历史45期沉降数据如表1所示。运用3种组合预测模型,以前35期数据为基础对其进行未来10期的预测,并与实际值比较,分析各模型的预测精度。

表1 地基实测沉降数据 mm
1.ARIMA模型预测
图3为地基沉降量未经差分和经一次和两次差分处理后的时间序列图。

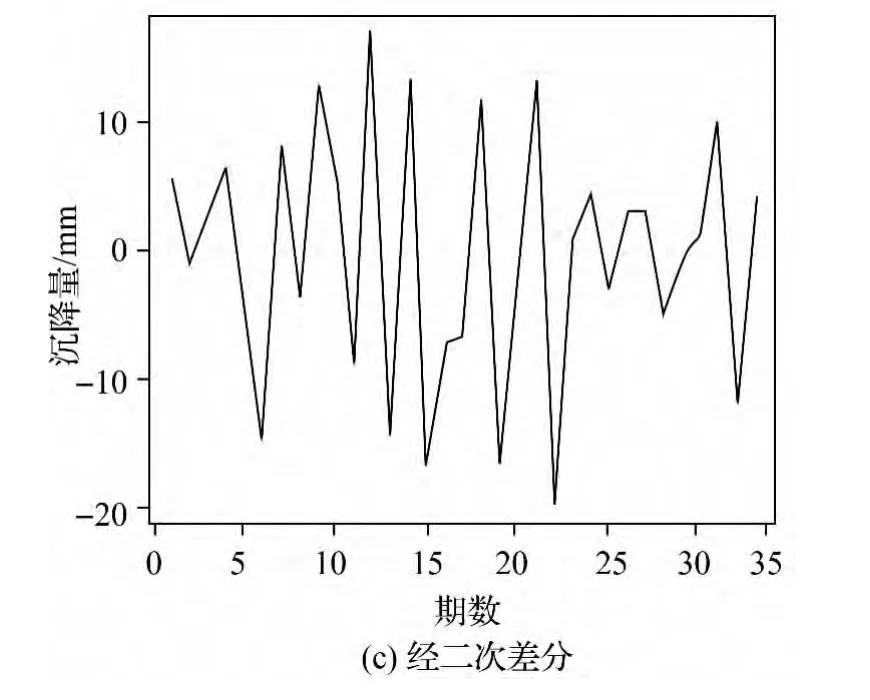
图3 沉降量未经差分和差分后序列图
由图3(a)可知,需进行差分处理。图3(c)为经二次差分后的时序图,可见序列基本平稳,因此确定ARIMA模型差分次数d=2。
先利用差分后序列的ACF图和PACF图进行初步判断,见图4。

图4 ACF图和PACF图
自相关和偏自相关函数的特征总结见表2。

表2 ARMA模型ACF和PACF的一般特征
可以看出ACF图和PACF图都是拖尾的,可初步判定差分后序列模型为ARMA模型。
输出差分序列的EACF图,如图5所示。

图5 EACF图
从图5可以看出,ARIMA(1,2,1)基本符合原始数据序列。
在利用极大似然估计法进行参数估计后,进行模型诊断,分析残差的正态性和自相关性并进行Ljung-Box检验,满足条件后根据 ARIMA(1,2,1)模型对原始序列进行未来10期的预测。预测结果及其误差见表3。
2.BP神经网络模型预测
采用滚动式[9]的预测方法来预测其误差。以1—5期沉降值为网络输入,第6期为网络输出。2—6期预测误差为网络输入,第7期为网络输出。以此类推到29—34期网络输入,35期为网络输出,组成样本进行网络训练。经过反复试验,选择隐含层神经元个数为15。部分Matlab代码如下

权值训练算法采用L-M优化算法[10],训练次数设为1000,训练精度为10-5,学习速率为0.01。网络经过154次训练到达最小误差(见图6),对该序列进行未来10期的预测,其结果见表3。
3.组合模型预测及分析
设ARIMA模型预测加权系数为k1,BP神经网络模型预测加权系数为k2,根据上文中的理论分别计算权系数。
以误差平方和最小组合模型计算得到权系数向量为

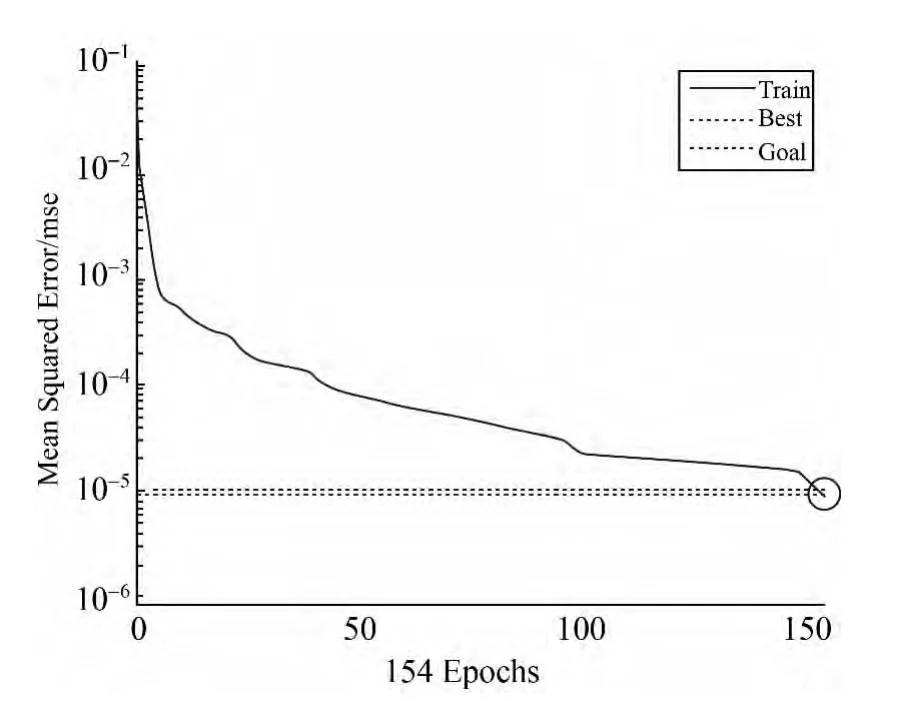
图6 BP神经网络误差曲线图
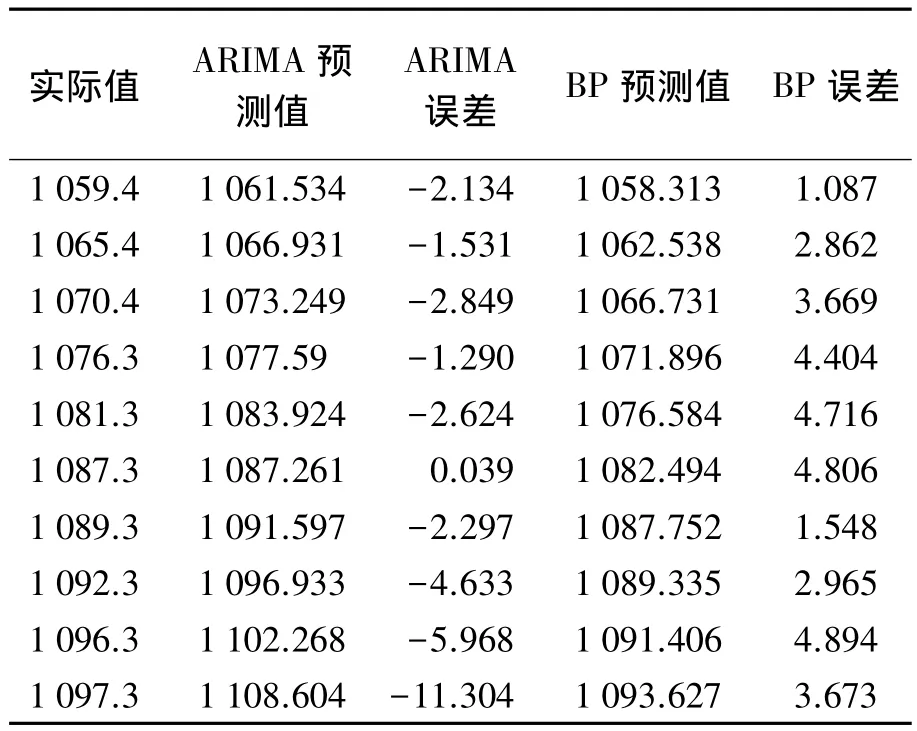
表3 ARIMA和BP神经网络单项模型预测值及误差mm
以调和平均组合模型计算得到权系数向量为
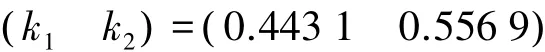
根据权系数向量即可计算以上两个组合模型的预测值及误差。
对序列线性和非线性规律单独描述的组合模型预测,先利用文中模型对历史数据的拟合值计算拟合误差,再利用BP神经网络法对误差进行未来10期的预测,方法同上,最后用拟合误差的预测值对ARIMA预测值进行修正,得到最终的预测值,结果见表4。
为了对比3种组合模型的预测精度,采用误差平方和(SSE)、均方误差(MSE)、平均绝对误差(MAE)这几项误差指标来度量。
误差平方和(SSE)
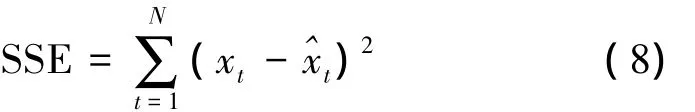
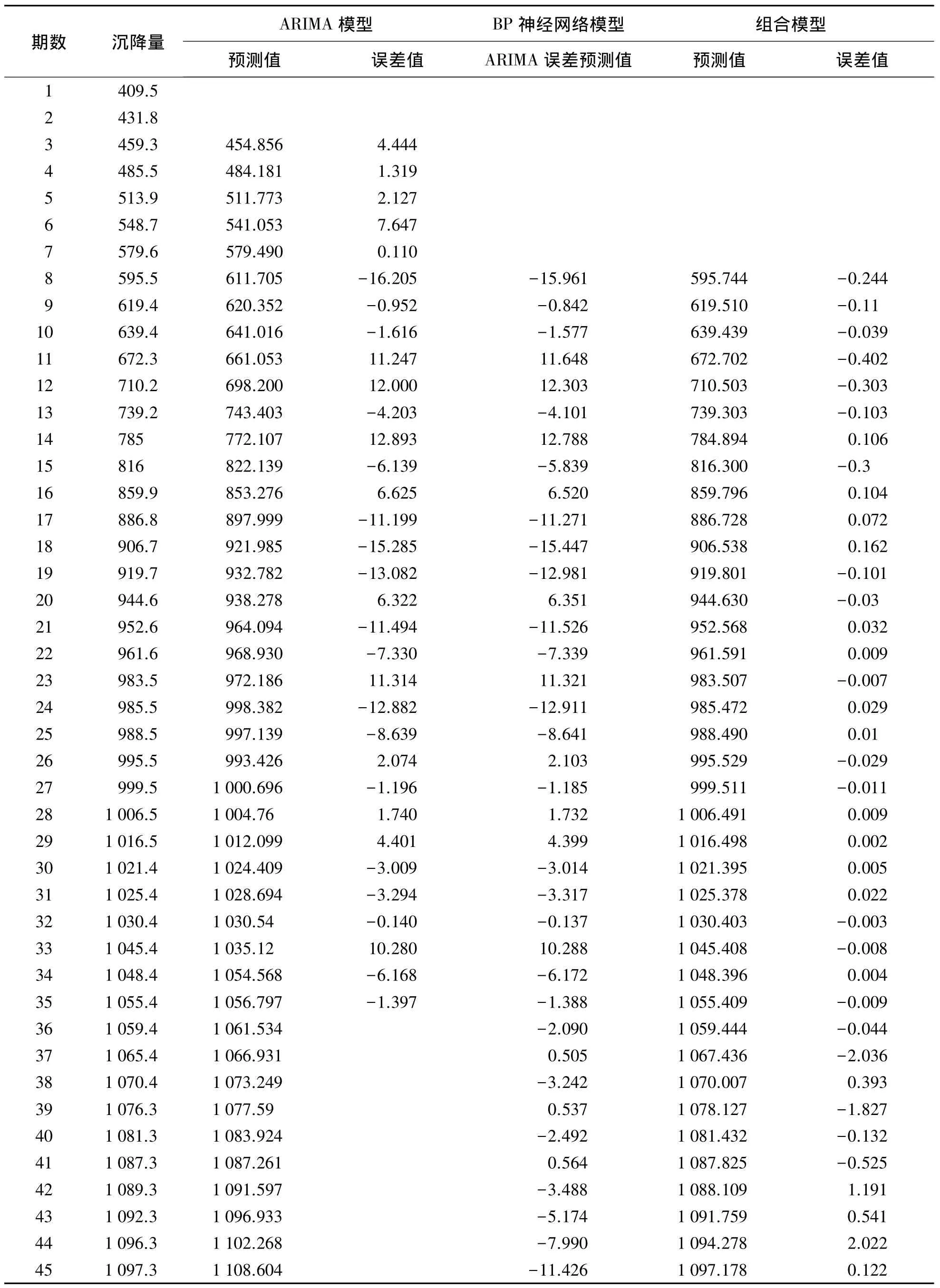
表4 组合模型预测结果mm
均方误差(MSE)
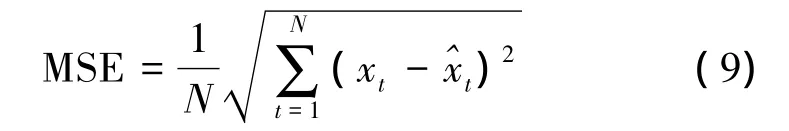
平均绝对误差(MAE)

计算得到3种组合模型的精度指标见表5。

表5 3种组合模型预测精度比较
其中组合模型1为误差平方和最小组合模型,组合模型2为调和平均组合模型,组合模型3为对序列线性和非线性规律单独描述的组合模型。
从表5可以看出,由于组合模型1和组合模型2的加权系数相差不大,因此精度也差不多,而组合模型3的精度相比之下有较大的提高,因此对序列线性和非线性规律单独描述的组合模型是相比各种加权组合模型更为可靠,是一种更有效的预测工具。
五、结 论
通过以上研究,主要得出以下几个结论:
1)误差平方和最小组合模型和调和平均组合模型比单一模型预测精度高,在一定程度上提高了预测的可靠性。
2)对序列线性和非线性规律单独描述的组合模型,把序列中的线性规律用时间序列法预测,再用BP神经网络法预测非线性规律的残差,最后把二者相加得到最终结果,从根本上提高了预测精度,比加权组合模型预测结果更可靠。
3)由于软土地基沉降的机理十分复杂,受到多种因素的影响,如施工过程中的预压时间、土体性质以及排水条件等,对沉降量的预测无法达到绝对严格的准确,预测结果仍然需要进一步的检验。
[1]冯春山,吴家春,蒋馥.石油价格的组合预测研究[J].石油大学学报:社会科学版,2004,20(1):12-14.
[2]CRYER JD,CHAN K S.时间序列分析及应用:R语言[M].北京:机械工业出版社,2011.
[3]李友坤.BP神经网络的研究分析及改进应用[D].淮南:安徽理工大学,2012.
[4]李聪.基于BP神经网络的股票指数期贷价格预测[D].青岛:青岛大学,2012.
[5]郑凤霞.基于神经网络和时间序列的预测方法及其应用研究[D].成都:电子科技大学,2012.
[6]陈华友,盛昭瀚,刘春林.调和平均的组合预测方法之性质研究[J].系统工程学报,2004(6):620-624.
[7]李磊.地基沉降预测方法分析[D].杭州:浙江大学,2004.
[8]黄声享,尹晖,蒋征.变形监测数据处理[M].武汉:武汉大学出版社,2003.
[9]雷可为,陈瑛.基于BP神经网络和ARIMA组合模型的中国入境游客量预测[J].旅游刊,2007,(4):20-25.
[10]李炯城,黄汉雄.神经网络中LMBP算法收敛速度改进的研究[J].计算机工程与用,2006,(16):46-50.

