北斗与GPS双系统测姿研究

邵 奎，白征东

(清华大学土木工程系，北京100084)

一、引 言

姿态测量作为导航系统的一个重要应用，已有的理论和算法都比较成熟。GPS作为最重要的数据源，在精度和实用性方面已经得到充分验证，北斗作为新兴的GNSS系统，以其作为数据源将成为必然趋势。然而，其在载体测姿方面，国内鲜有学者对其精度和稳定度作过详细研究。

本文使用北斗数据作为数据源求解载体姿态，在试验处理中，使用同源GPS数据对姿态进行解算，并将两者的结果进行对比分析，得出北斗系统作为数据源在姿态解算应用上的可行性和精度信息，进一步分析表明，北斗数据解算结果无论精度还是稳定度都不输于GPS系统，甚至在一些情况下优于GPS系统。

二、数据模型和算法

姿态角求解的核心是坐标系的旋转变换，站心直角坐标系到载体坐标系的变换可以通过绕坐标轴的3次旋转实现，3次的旋转角分别为偏航角(yaw)、俯仰角(pitch)和翻滚角(roll)，旋转后的站心直角坐标系和载体坐标系重合。

本文使用3台接收机构成双基线同时求取3个姿态角。实际中可根据不同情况选择不同的接收机位置，不同的位置选择将直接影响到计算模型和姿态角求取公式的不同［1］。本文中，主接收机位于载体坐标系原点，从1接收机位于载体坐标系Y轴，从2接收机位于XOY平面，与Y轴夹角为θ。

目前的姿态算法可分为两类，即基于基线求解的姿态算法和基于滤波的姿态算法。基于基线求解的姿态算法又可以分为直接法、姿态矩阵最小二乘法和姿态角最小二乘法。其中，直接法因其简单有效获得了广泛应用，本文采用直接法求取姿态角［2］。

载体坐标系到站心坐标系的转换可用如下公式表示

式中，Xl为站心坐标系坐标，由空间直角坐标旋转得到，见式(2)。Xb为载体坐标系，是固定值，不随时间改变，根据本文试验接收机位置，其具体形式见式(3)

式(1)中未知量为y、p、r 3个姿态角，将式(2)和(3)代入式(1)中，进行矩阵相乘后，可以得到

三、试验及结果分析

为了得到北斗数据在姿态解算上的可行性和精度，本文设计了试验加以求解。为了获得稳定姿态角预期，试验以静态方式进行。本文使用BD/GPS双系统接收机同时采集数据，然后分别进行测姿处理，最后进行对比分析。在处理方法上，采用双差kalman滤波求解基线［3］，其他误差，如对流层和电流层误差，采用相同算法和处理模型［4］，具体见表1。

表1 程序参数设置

1.试验结果对比

下图中，为了有效地显示，剔除了整周模糊度未固定之前的数据，以下各图均从开始观测后的两百个历元起始。

图1 北斗与GPS系统YAW解算结果

图2 北斗与GPS系统PITCH解算结果

图3 北斗与GPS系统ROLL解算结果

解算结果统计信息如表2所示，表中分别列出测量平均值、标准差、数据剔除率和最大误差［5］。平均值的差异表现出两系统结果的系统差异，标准差的对比显示了系统测量的稳定程度，数据剔除率显示了测量数据的有效性，最大误差在一定程度上能够反映测量数据粗差情况。

表2 试验统计数据(°)

表2中同一组数据里前者为北斗结果，后者为GPS结果。

数据淘汰率是以所有观测数据为样本，求取中误差，极限误差选取3倍中误差，落在极限误差外的数据视为无效数据，进行淘汰，数据淘汰率是淘汰数据占全部数据的比率［6］。

为了更清查表达两系统解算结果的差异，将GPS的解算结果同北斗解算结果做差，得到偏航角yaw、俯仰角pitch和翻滚角roll在对应历元下的差异，用图表示如下。

图4 YAW结果差异图

图5 PITCH结果差异图

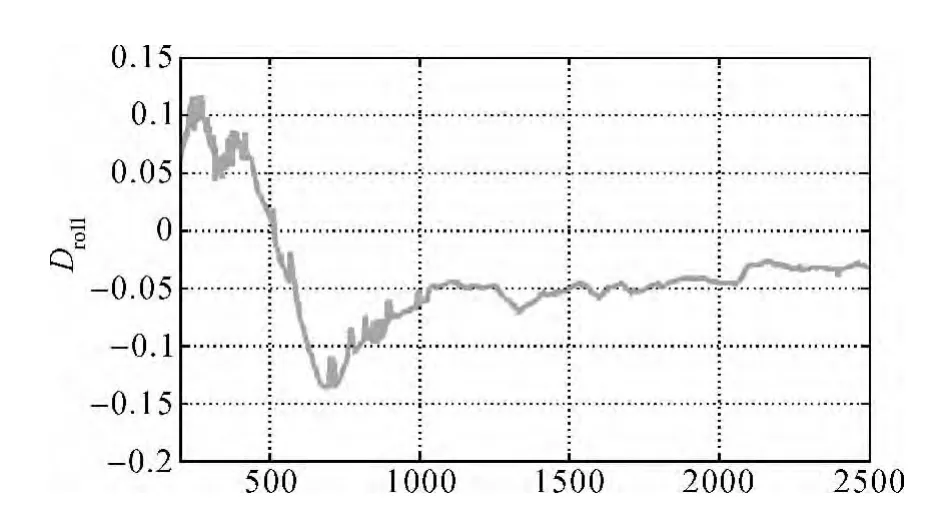
图6 ROLL结果差异图

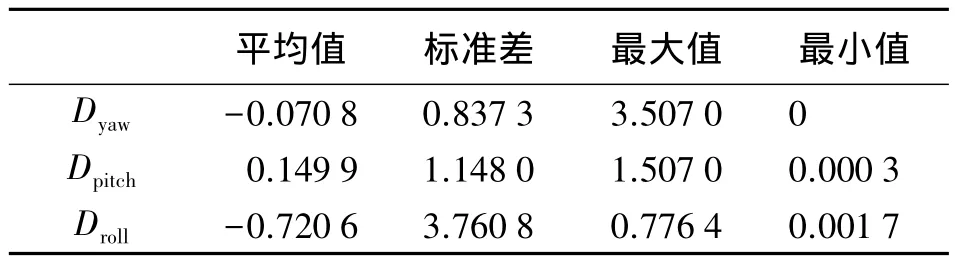
表3 姿态角差值统计信息(°)

2.试验结果分析

根据误差传播定律和姿态角计算公式，偏航角yaw、俯仰角pitch和翻滚角roll误差应依次递增，姿态角对应的两系统的差值和标准差也应依次递增，这与表2和表3中结果相符［7］。

分析表2，北斗系统的yaw、pitch和roll标准差分为 0.039 6°、0.207 5°和0.530 3°，而 GPS 系统的对应值分别为 0.258 7°、0.152 8°和0.629 6°，可以看出，北斗在偏航角和翻滚角解算上稳定度略高于GPS，俯仰角稳定性稍弱GPS，但总体相差并不大，稳定性相当。

在最大误差方面，北斗数据的yaw、pitch和roll分别为 1.168 1°，3.038 0°和4.350 2°。对应的 GPS最大误差分别为 1.835 7°、1.384 8°和6.189 0°，最大误差受到观测条件和偶发事件的影响较大，具有较大不确定性，但仍能够反映两系统控制粗差的能力，从上述数据看，两系统粗差相当，且北斗系统略优于GPS系统。

在数据淘汰率方面，北斗数据的偏航角、俯仰角和翻滚角分别为 2.887 9°、0.770 1°和2.733 9°。对应GPS 的三姿态分别为 1.116 7°、1.771 3°和1.039 7°。数据剔除率是有效数据所占的比例，反映了观测数据的质量，从以上数据分析，北斗系统的偏航角和翻滚角剔除率是GPS系统的两倍左右，而俯仰角则优于GPS，但总体上看，GPS系统优于北斗系统。

分析表格3，差值平均值能够反映两系统的系统差值，从表中可看出，翻滚角的差值最大，为-0.720 6°，在0.01弧度级别上。无论观察试验图形还是上表中的统计数据，可以发现，北斗与GPS系统具有明显的系统差异，但差异均不超过百分之一弧度级别。

3.补充试验

接收机接受卫星信号受到观测时间、观测地点、观测环境等影响，分析一次观测结果所得到的结论不能不具有充足的可信性，为了验证上面的试验结果分析，作者先后不同时间，不同地点进行了3组重复的试验观测，试验结果如下表所示。

表4 补充试验1统计结果(°)

表5 补充试验1差分统计结果(°)

表6 补充实验2统计结果(°)

表7 补充试验2差分统计结果(°)

表8 补充试验3统计结果(°)

表9 补充试验3差分统计结果(°)

受观测条件和时间等的影响，补充试验所得数据精度和稳定度变动较大，同原试验中的结果存在差异。上文中的每一项具体试验结果分析不一定能够在补充试验中得到证明，如原试验中俯仰角pitch的北斗数据标准差大于GPS数据标准差，但在补充试验1和补充试验2中则正好相反。

但通过上表分析可知，某一项具体统计信息的优劣具有随机性，不同的试验可能得到不同的结果。但所有试验分析结果都显示，两个系统所得的3个姿态角的各项数值标准均在同一个数量级上，并随着不同的试验而呈现随机的变化。这表明，在载体测姿应用中，北斗系统在精度、稳定度和控制粗差等方面性能均可以达到GPS系统级别，甚至在一些情况下优于后者。

四、总 结

北斗作为我国独立的卫星导航系统，将其作为载体姿态测量的数据源具有巨大战略意，同时，其独特的卫星系统设计使得在我国领土内信号具有更好的覆盖和强度，使用北斗作为数据源具有必然性。

本文对双基线直接法测量载体姿态进行了理论公式推导，为了得到北斗测姿的精度和稳定度等信息，设计并实施了4组试验，通过对试验进行统计，得到如下结论:

1)对于3个姿态角，北斗和GPS系统在精度、稳定度和控制粗差能力等指标的优劣具有随机性，在不同试验中会得出不同结果。

2)姿态角各项数据指标优劣具有一致性。对于具体某一次试验，3个姿态角会呈现相同趋势，比如原始实验中北斗系统统计结果中偏航角、翻滚角标准差优于GPS系统统计结果，而俯仰角则较差，那么其他指标，如数据剔除率，基本会表现出同样情况。

3)所有试验结果都表明，在载体测姿应用中，北斗系统在精度、稳定度和控制粗差等方面性能均可以达到GPS系统级别，甚至在一些情况下优于后者。

［1］HOFMANNWB，LICHTENEGGERH，WASLEE.GNSS:Global Navigation Satellite Systems:GPS，GLONASS，GALILEO，and More［M］.Berlin:Springer，2008.

［2］王潜心.机载GPS动态定位定速与定姿理论研究及软件开发［D］.长沙:中南大学，2011.

［3］TAKASU T，YASUDA A.Kalman-filter-based Integer Ambiguity Resolution Strategy for Long-baseline RTK with Ionosphere and Troposphere Estimation［C］∥Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation.Oregon:［s.n.］，2010.

［4］LI Y，ZHANG K，ROBERTSC，et al.On-the-fly GPS-based Attitude Determination Using Single-and Doubledifferenced Carrier Phase Measurements［J］.GPS Solutions，2004，8(2):93-102.

［5］CHEN W，QIN H.New Method for Single Epoch，Single Frequency Land Vehicle Attitude Determination Using Low-end GPS Receiver［J］.GPS solutions，2012，16(3):329-338.

［6］TEUNISSEN P，GIORGI G，BUIST P J.Testing of a New Single-frequency GNSS Carrier Phase Attitude Determination Method: Land， Ship and Aircraft Experiments［J］.GPSsolutions，2011，15(1):15-28.

［7］陈杨，唐艳，周伟，等.三天线GPS姿态解算误差分析［J］.全球定位系统，2012，37(3):16-18.